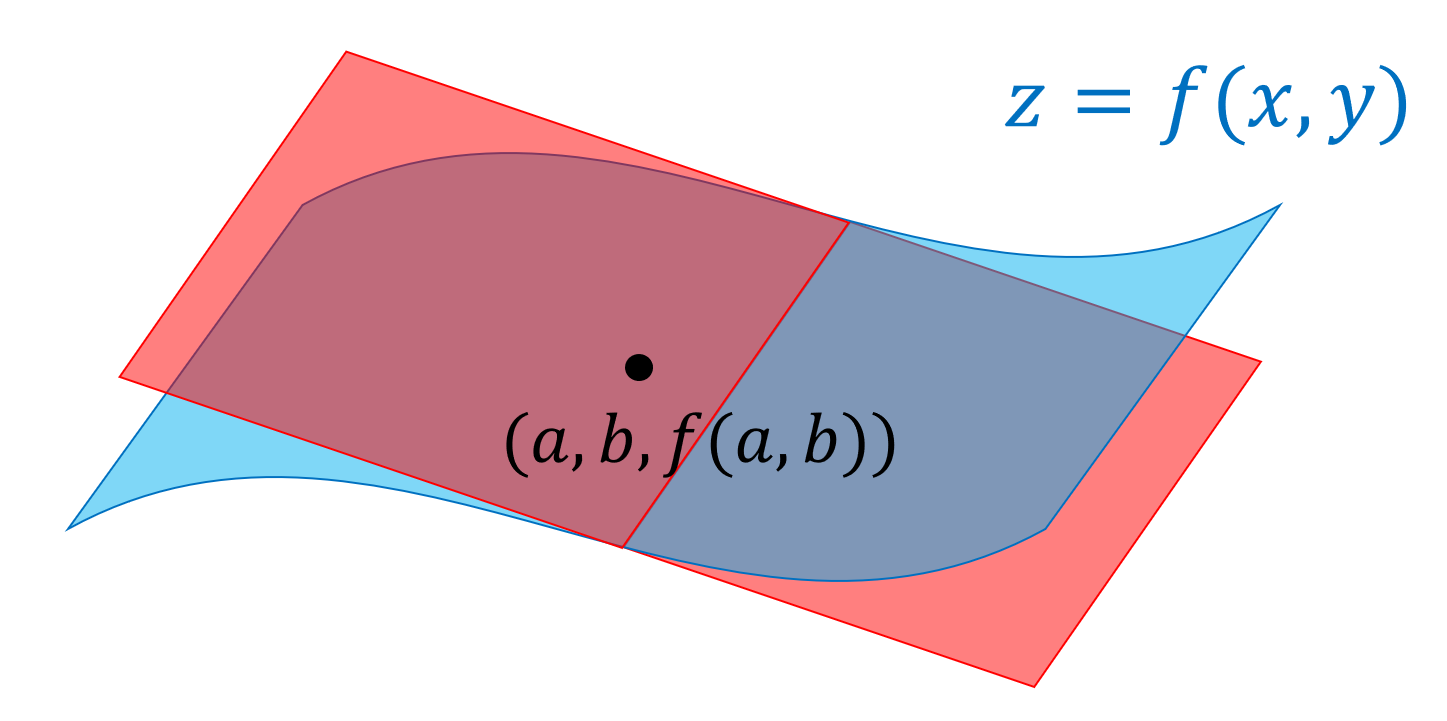
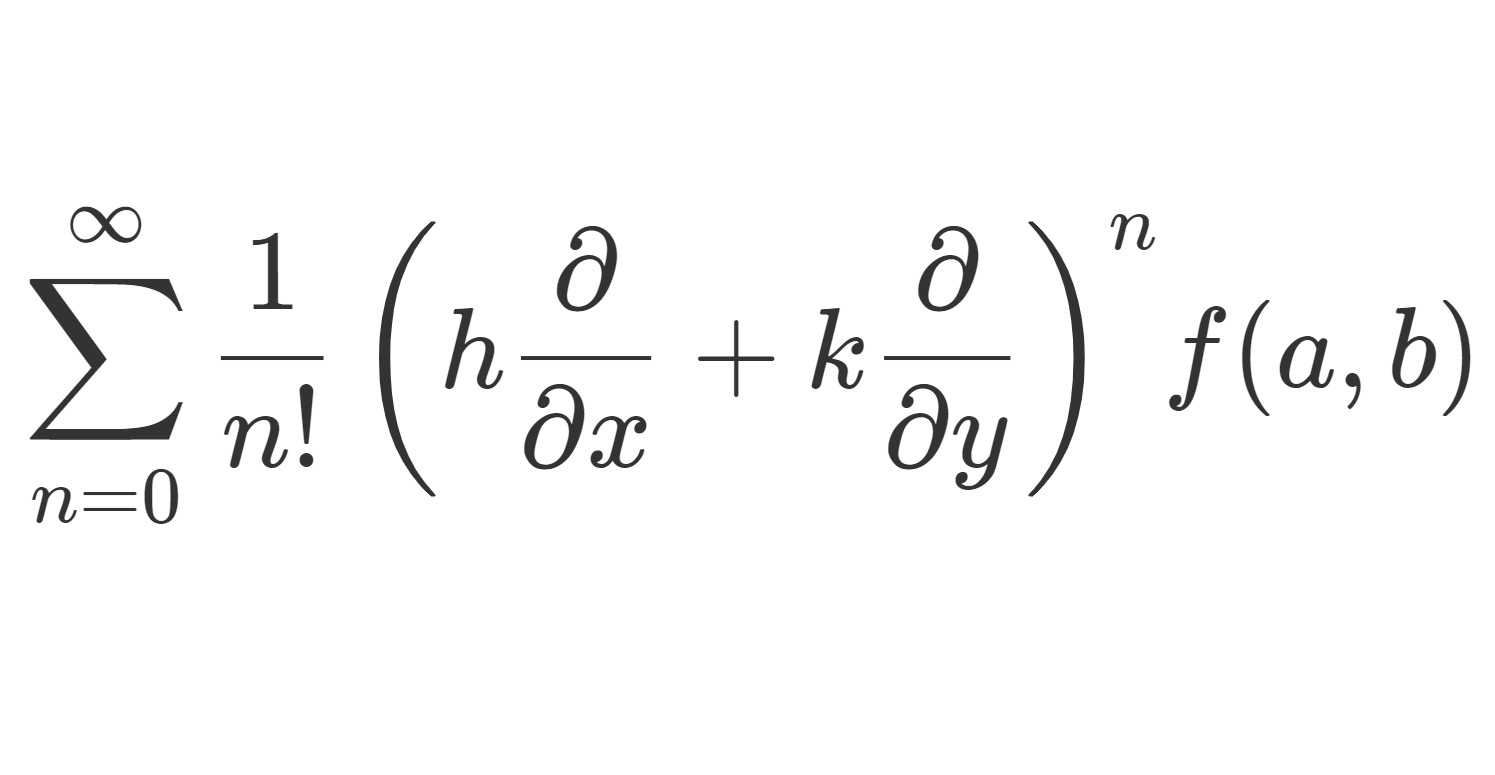2変数関数 f(x,y) の点 (a,b) におけるテイラー展開は
f(a+h,b+k)=\sum_{n=0}^\infty \frac{1}{n!}\left(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y}\right)^n \! f(a,b)
とかけます。本記事では,このような2変数,あるいはより一般に多変数におけるテイラーの展開・マクローリン展開を,テイラーの定理・マクローリンの定理も同時に述べながら解説します。
2変数におけるテイラー展開・マクローリン展開
まずは,2変数におけるテイラーの定理・マクローリンの定理を考え,それからテイラー展開・マクローリン展開を述べましょう。
2変数におけるテイラーの定理・マクローリンの定理
以下では簡単のため, f\colon \mathbb{R}^2\to\mathbb{R} としましょう。
定理(2変数におけるテイラーの定理)
f(x,y) は C^n 級であるとし,
\color{red}\begin{aligned}&f(a+h,b+k)\\&=\sum_{m=0}^{n-1} \frac{1}{m!}\left(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y}\right)^m f(a,b) +R_n \end{aligned}
としたとき,\displaystyle \color{red}R_n = \frac{1}{n!} \left( h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y} \right)^n f(a+\theta h, b+\theta k) となる 0<\theta <1 が存在する。
このときの R_n を剰余項という。
上の定理において, a=b=0 としたものがマクローリンの定理です。
定理(2変数におけるマクローリンの定理)
f(x,y) は C^n 級であるとし,
\color{red}\begin{aligned}&f(h,k)\\&=\sum_{m=0}^{n-1} \frac{1}{m!} \left(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y}\right)^m f(0,0) +R_n \end{aligned}
としたとき,\displaystyle\color{red} R_n = \frac{1}{n!} \left( h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y} \right)^n f(\theta h, \theta k) となる 0<\theta <1 が存在する。
ここで,
\begin{aligned} &\left(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y}\right)^m\\ &= \sum_{r=0}^m {}_m \mathrm{C}_r \,h^{m-r}k^r \frac{\partial^m }{\partial x^{m-r} \partial y^r} \end{aligned}
の意味です。二項定理ですね。
テイラーの定理の証明は,後で行うことにしましょう。
これを無限和に拡張したものがテイラー展開・マクローリン展開です。その定義を述べましょう。
2変数におけるテイラー展開・マクローリン展開
定義(2変数におけるテイラー展開)
f は C^\infty 級であるとする。テイラーの定理において, R_n \xrightarrow{n\to\infty} 0 であるとき,
\color{red}\begin{aligned}&f(a+h,b+k)\\&=\sum_{n=0}^{\infty} \frac{1}{n!} \left(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y}\right)^n \! f(a,b) \end{aligned}
と表せる。これを (a,b) のまわりのテイラー展開 (Taylor expansion) という。任意の点のまわりでテイラー展開可能であるとき, f は解析的 (analytic) であるという。
定義(2変数におけるマクローリン展開)
f は C^\infty 級であるとする。マクローリンの定理において, R_n \xrightarrow{n\to\infty} 0 であるとき,
\color{red}\begin{aligned}f(h,k)=\sum_{n=0}^{\infty} \frac{1}{n!} \left(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y}\right)^n f(0,0) \end{aligned}
と表せる。これをマクローリン展開 (Maclaurin expansion) という。
注意ですが, C^\infty 級だからといって解析的(テイラー展開可能)とは限りません。これは,一変数のときの例が有名です。テイラー展開・マクローリン展開とは【解析的な関数と具体例】のラストの方で解説しています。
2変数におけるテイラーの定理の証明
テイラーの定理を証明しておきましょう。
証明は, t\mapsto f(a+th, b+tk) のように一変数関数と思って,一変数のときのテイラーの定理を適用すればよいです。
証明
\varphi(t)=f(a+th, b+tk) とおく。すると,一変数のときのテイラーの定理から,ある 0<\theta <1 が存在して,
\varphi(1)=\sum_{m=0}^{n-1}\frac{\varphi^{(m)}(0)}{m!}+\frac{1}{n!}\varphi^{(n)}(\theta)\tag{1}
とできる。合成関数の偏微分の連鎖公式(チェインルール)から,
であるため,これを (1) 式に代入すればよい。
証明終
証明は,思ったより短く感じたかもしれませんね。
多変数におけるテイラー展開・マクローリン展開
より一般に, f\colon \mathbb{R}^d \to\mathbb{R} の場合のテイラー展開・マクローリン展開について述べておきましょう。
多変数におけるテイラーの定理・テイラー展開
f は C^n 級であるとすると,
\color{red} \begin{aligned}&f(a_1+h_1, \dots, a_d+h_d)\\ &=\sum_{m=0}^{n-1} \frac{1}{m!} \left(h_1\frac{\partial }{\partial x_1}+\dots + h_d\frac{\partial }{\partial x_d}\right)^m \\ &\qquad f(a_1,\dots, a_d)+R_n,\\ R_n&= \frac{1}{n!} \left(h_1\frac{\partial }{\partial x_1}+\dots + h_d\frac{\partial }{\partial x_d}\right)^n \\ &\qquad f(a_1+\theta h_1,\dots, a_d+\theta h_d) \end{aligned}
となる 0<\theta <1 が存在する。 このときの R_n を剰余項という。
また, f が C^\infty 級で R_n\xrightarrow{n\to\infty} 0 のときは,
\color{red} \begin{aligned}&f(a_1+h_1, \dots, a_d+h_d)\\ &\!\!=\!\! \sum_{n=0}^{\infty}\! \frac{1}{n!} \!\! \left(\!h_1\frac{\partial }{\partial x_1}+\dots + h_d\frac{\partial }{\partial x_d}\!\right)^n\!\!\! f(a_1,\dots, a_d) \end{aligned}
と表せ,これを (a_1,\dots, a_n) のまわりのテイラー展開 (Taylor expansion) という。
n 乗の部分は,多項定理を用いて展開したものを形式的に表現しています。
ここで, \boldsymbol{a}=(a_1,\dots, a_d),\; \boldsymbol{h}=(h_1,\dots, h_d) を d 次元ベクトルとし, \nabla = (\frac{\partial}{\partial x_1}, \dots, \frac{\partial}{\partial x_d}) を微分演算子とすると,テイラー展開は
\color{red} f(\boldsymbol{a}+\boldsymbol{h}) =\sum_{n=0}^\infty \frac{1}{n!}(\boldsymbol{h}\cdot \nabla)^n f(\boldsymbol{a})
とスッキリかけます。ここで, \cdot は内積を指します(→数ベクトルの定義と数ベクトルにおけるノルム・内積)。
上で, \boldsymbol{a}=\boldsymbol{0} としたものがマクローリンの定理・マクローリン展開です。
多変数におけるマクローリンの定理・マクローリン展開
f は C^n 級であるとすると,
\color{red} \begin{aligned}&f(h_1, \dots, h_d)\\ &=\sum_{m=0}^{n-1} \frac{1}{m!} \left(h_1\frac{\partial }{\partial x_1}+\dots + h_d\frac{\partial }{\partial x_d}\right)^m \\ &\qquad f(0,\dots,0)+R_n,\\ R_n&= \frac{1}{n!} \left(h_1\frac{\partial }{\partial x_1}+\dots + h_d\frac{\partial }{\partial x_d}\right)^n \\ &\qquad f(\theta h_1,\dots, \theta h_d) \end{aligned}
となる 0<\theta <1 が存在する。
また, f が C^\infty 級で R_n\xrightarrow{n\to\infty} 0 のときは,
\color{red} \begin{aligned}&f(h_1, \dots, h_d)\\ &\!=\! \sum_{n=0}^{\infty} \!\frac{1}{n!} \!\!\left(h_1\frac{\partial }{\partial x_1}+\dots + h_d\frac{\partial }{\partial x_d}\right)^n\!\! f(0,\dots, 0) \end{aligned}
と表せ,これをマクローリン展開 (Maclaurin expansion) という。
テイラー展開のときと同じくスッキリかくと
\color{red} f(\boldsymbol{h}) =\sum_{n=0}^\infty \frac{1}{n!} ( \boldsymbol{h}\cdot \nabla)^n f(\boldsymbol{0})
ですね。
多変数におけるテイラーの定理の証明は,2変数のときとほぼ同じですから,省略します。