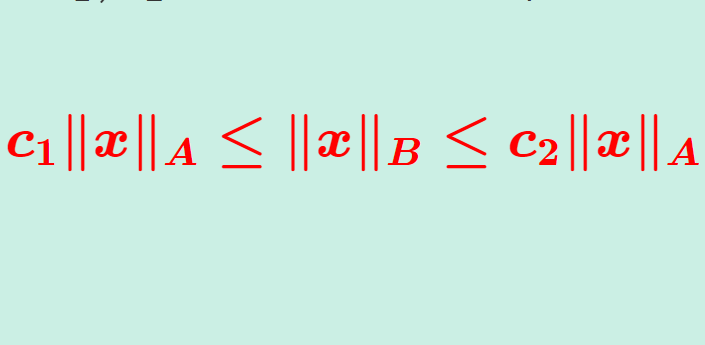あるベクトル空間には,複数のノルムの定め方があります。しかし,それらのノルムは結局同じ「収束」を扱うことになる場合があります。このとき,ノルムは同値であるといいます。
ノルムの同値性の具体的な定義と,有限次元ベクトル空間のノルムは全て同値であること,また,逆に無限次元ベクトル空間ではノルムが同値にならないことがあることを紹介します。
ノルムの同値性
定義(ノルムの同値性)
X をベクトル空間とし,\|\cdot \|_A と \|\cdot \|_B をその上の2つのノルムとする。この2つのノルムが同値 (equivalent) であるとは,ある c_1,c_2>0 が存在して,
\color{red}\boldsymbol{ c_1 \|x\|_A\le \|x\|_B\le c_2\|x\|_A ,\quad x\in X}
とできることをいう。
c_1,c_2>0 は x\in X に依らないことが大切です。
ノルムが同値であるとき, \|\cdot\|_A で x_n\to x となることと, \|\cdot\|_B で x_n\to x となることが同値になります。実際,
\|\cdot\|_A で x_n\to x を仮定すると,
\|x_n-x\|_B\le c_2 \|x_n-x\|_A \xrightarrow{n\to\infty} 0
なので \|\cdot\|_B で x_n\to x が言え,逆に \|\cdot\|_B で x_n\to x を仮定すると,
となるため, \|\cdot\|_A で x_n\to x となりますね。ノルムが同値とは,収束の概念が同じということであり,難しく言えば,距離が誘導する位相的性質が同じということです。
なお, \|\cdot\|_A と \|\cdot\|_B が同値であり,かつ \|\cdot\|_B と \|\cdot\|_C が同値であるとき, \|\cdot\|_A と \|\cdot\|_C が同値であることは容易に確認できます。要するに,「ノルムの同値」という関係は,同値関係になっているということです。
有限次元空間上のノルムは全て同値
ノルムの定め方はいろいろありますが,有限次元においては全て同値であるというのが次の定理です。
\mathbb{C} 上としましたが, \R 上でも同様です。証明しておきましょう。
証明
\dim X=n とし, \{x_1, x_2,\dots, x_n\} を一つの基底とする。このとき,任意の x\in X は x=k_1x_1+k_2x_2+\cdots +k_nx_n\;\;(k_1,k_2,\dots, k_n\in\mathbb{C}) と表せる。このとき,
\|x\|_\infty = \max_{1\le j\le n} |k_j|
と定めると,これはノルムになる。このノルムがその他の任意のノルムと同値であることを示せばよい。そこで,別のノルム \|\cdot\| をとる。
まず, c_1 \|x\|\le \|x\|_\infty を示そう。
x=k_1x_1+k_2x_2+\cdots +k_nx_n\;\;(k_1,k_2,\dots, k_n\in\mathbb{C}) とすると,
\|x\| \le \sum_{j=1}^n |k_j|\|x_j\| \le \|x\|_\infty \sum_{j=1}^n \|x_j\|
より, c_1 = \left(\sum_{j=1}^n \|x_j\|\right)^{-1} とすればよい。
次に, \|x\|_\infty\le c_2\|x\| を示そう。
背理法で示す。もしこのような定数 c_2>0 が存在しないとすると \|x\|_\infty/\|x\| が有界でないから,任意の整数 m>0 に対し,ある y_m\in X\setminus\{0\} が存在して, \|y_m\|_\infty/\|y_m\| \ge m とできる。言い換えると \|y_m\|/\|y_m\|_\infty \le 1/m である。
z_m = y_m /\|y_m\|_\infty とすると, \|z_m\|_\infty=1 かつ \| z_m\|\le 1/m である。
z_m = k_1^{(m)}x_1+\dots + k_n^{(m)} x_n
と基底を用いて表すと,\| z_m\|_\infty = 1 より, k_1^{(m)}, k_2^{(m)}, \dots, k_n^{(m)} のうち,少なくとも一つの絶対値が 1 である。さらに任意の m についてこのことが成立するから,数列 \{k_1^{(m)}\}_m, \{k_2^{(m)}\}_m, \dots, \{k_n^{(m)}\}_m のうち,絶対値が 1 となる項が無限個あるものが一つ存在する。それを \{k_j^{(m)}\}_m とする。
\{k_j^{(m)}\}_m の各項のうち,絶対値が 1 になるもののみを取り出し,さらに \| k_i^{(m)}\| \le 1\; (i\ne j) より,ボルツァノ–ワイエルシュトラスの定理より,点列 (k_1^{(m)},\dots, k_n^{(m)}) は収束する部分列をもつので,それを \{k_j^{(m_l)}\}_l とする。 k_i^{(m_l)}\to k_i \; (l\to\infty) とする。
z = k_1x_1+\dots + k_n x_n
と定めると, \|z_{m_l}-z\|_\infty \to 0 \; (l\to\infty) である。前半の証明より, \|z_{m_l}-z\| \to 0 \; (l\to\infty) となる。したがって,
より, z=0 である。一方で,| k_j| =1,\, |k_i|\le 1 \;(i\ne j) なので \|z\|_\infty =1 で,これは矛盾している。したがって,示せた。
証明終
後半は少々難しいかもしれませんね。どっちのノルムを扱っているのか,常に注意しながら読み進めましょう。
同値なノルムでない例
ノルムが同値でない例を挙げておきましょう。有限次元ベクトル空間のノルムは全て同値でしたから,ここで挙げる例は無限次元ベクトル空間です。
同値なノルムでない例
C[0,1] を [0,1] 上連続関数の空間とする。このとき, f\in C[0,1] に対し,
\color{red}\begin{aligned} \|f\|_\infty &= \sup_{0\le x\le 1} |f(x)|, \\ \|f\|_1 &= \int_0^1 |f(x)|\, dx\end{aligned}
と定めると, \|\cdot\|_\infty,\; \|\cdot\|_1 はどちらもノルムになるが,同値ではない。
ノルムになることは置いておくことにして,これが同値でないことを示しましょう。f_n = 1_{[0,1/n]},\; f=0 と定めます(ただし 1 は定義関数(特性関数))。 このとき,
\|f_n-f\|_\infty = \sup_{0\le x\le 1}| 1_{[0,1/n]}|=1
ですから, f_n と f の「距離」はずっと 1 です。一方で
ですから, \|\cdot\|_1 では f_n\to f になります。同値なノルムは,収束の概念が一致していなければなりませんでしたから,これらのノルムは同値でないとわかりますね。