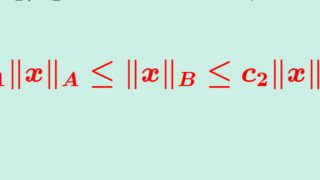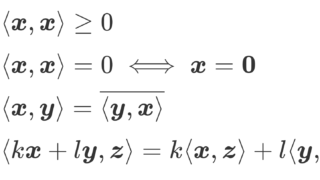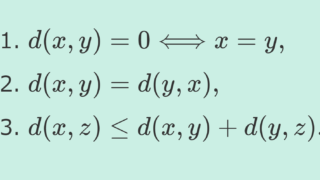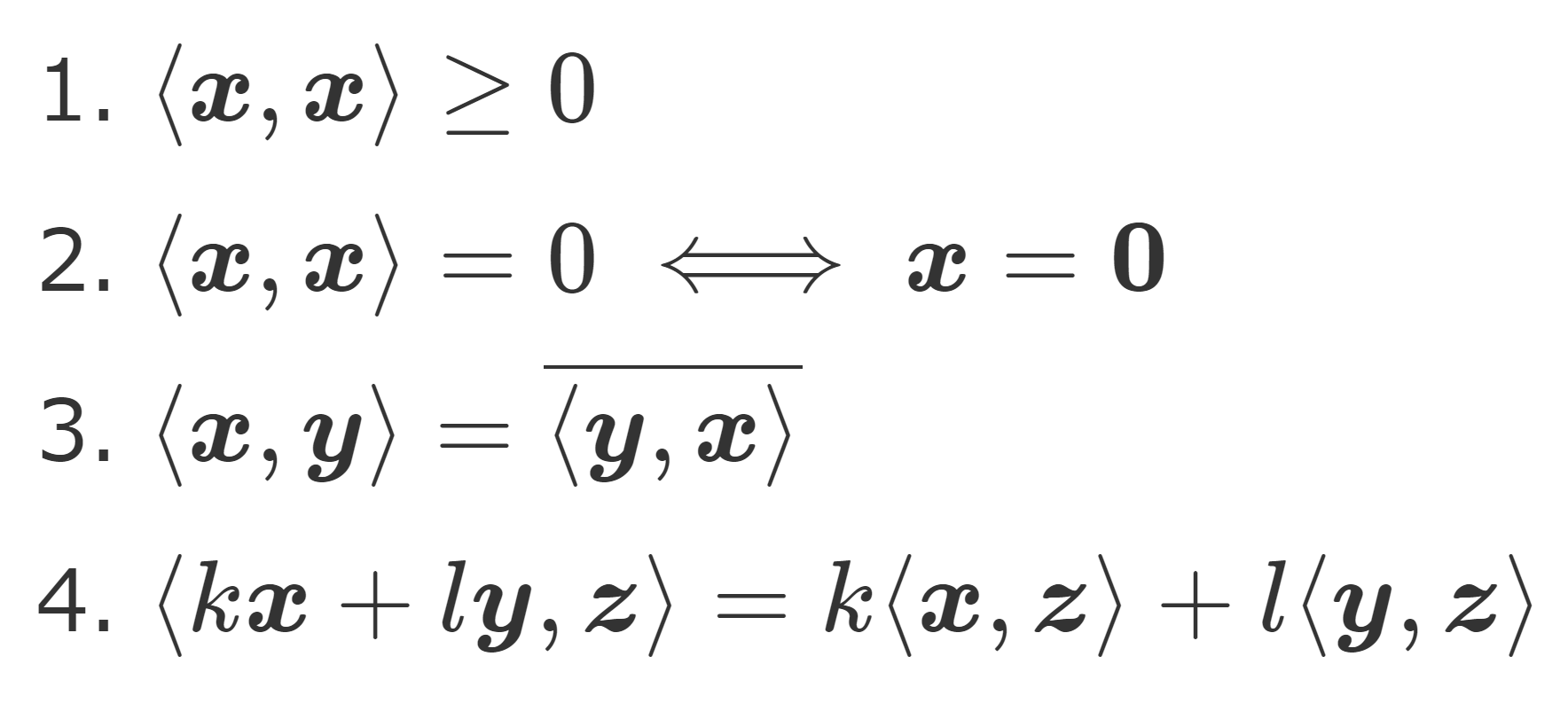ノルムとは～ノルム空間の定義と具体例～

ノルムとは，ベクトルの大きさを定める量のようなものです。ノルムを定義することで，ベクトル同士の「距離」を考えることができるようになり，収束の議論ができるようになります。

ノルム・ノルム空間の定義を述べ，その簡単な具体例を紹介しましょう。

ノルムとは～ノルム空間の定義～
ノルム空間の簡単な例
ノルムはベクトル空間上に距離を定める
さらなる発展
1. 内積が定義された空間
2. 完備なノルム空間
関連する記事

ノルムとは～ノルム空間の定義～

定義（ノルム空間）

以下， $K=\mathbb{R}$ または $\mathbb{C}$ とする。

$K$ 上ベクトル空間 $V$ がノルム空間 (normed space) であるとは，以下の条件をみたすノルム (norm) と呼ばれる関数 $\lVert \cdot\rVert\colon V\ni \boldsymbol{x}\mapsto \lVert \boldsymbol{x}\rVert\in \mathbb{R}$ が定義されていることをいう。
(以下で， $\boldsymbol{x,y}\in V,\; k\in K$ とする。)

$\lVert \boldsymbol{x}\rVert \ge 0$
$\lVert \boldsymbol{x}\rVert = 0\iff \boldsymbol{x}=\boldsymbol{0}$
$\lVert k\boldsymbol{x}\rVert =| k|\lVert\boldsymbol{x}\rVert$ (斉次性)
$\lVert \boldsymbol{x}+\boldsymbol{y}\rVert\le \lVert \boldsymbol{x}\rVert +\lVert \boldsymbol{y}\rVert$ (三角不等式)

ノルムと呼ばれる関数が定義されているベクトル空間がノルム空間です。

$\lVert \cdot \rVert \colon V\to \R$ と書きましたが， $\lVert \boldsymbol{x}\rVert \ge 0$ なので， $\lVert \cdot \rVert \colon V\to [0,\infty)$ とも書けますね。

なお，上の1,3,4.のみ成り立ち，2.が成り立つか不明なものをセミノルム (semi-norm; 半ノルム) といいます。本記事ではセミノルムは扱いません。

ノルム空間の簡単な例

数ベクトルと呼ばれる，数字の並びで表せるベクトル空間におけるノルムの例を紹介しましょう。

例1(絶対値ノルム).

$\mathbb{R}$ を $\mathbb{R}$ 上のベクトル空間とみる。 $x,y,k\in\R$ に対し，

$|x|\ge 0$
$|x|=0\iff x=0$
$|kx|=|k||x|$
$|x+y|\le |x|+|y|$

が成立するため，絶対値関数はノルムである。

実数値をベクトルと見たとき，その上の絶対値を取る関数はノルムの定義をみたしています。

なお， $\mathbb{C}$ を $\mathbb{C}$ 上のベクトル空間とみても，絶対値は同じようにノルムになります。

例2(ユークリッドノルム・ $\ell^2$ ノルム).

$\R^2$ を $\R$ 上のベクトル空間とみる。 $\boldsymbol{a}= (x,y)\in \R^2$ に対し，

\color{red}\lVert \boldsymbol{a}\rVert_2 = \sqrt{x^2+y^2}

と定めると，これはノルムになる。実際，

$\lVert \boldsymbol{a}\rVert_2\ge 0$
$\lVert \boldsymbol{a}\rVert_2=0\iff \boldsymbol{a}=\boldsymbol{0}$
$\lVert k \boldsymbol{a}\rVert_2=|k|\|\boldsymbol{a}\|_2$
$\| \boldsymbol{a}+ \boldsymbol{b}\|_2\le \| \boldsymbol{a}\|_2+\| \boldsymbol{b}\|_2$

のうち，1,2,4.は明らかであり，3.については， $\boldsymbol{a}=(x,y)$ に対し，

\begin{aligned}\lVert k \boldsymbol{a}\rVert_2 &= \| (kx,ky)\|_2\\& = \sqrt{(kx)^2+(ky)^2} \\&= |k|\sqrt{x^2+y^2} \\&= |k| \| \boldsymbol{a}\|_2 \end{aligned}

なので，成立している。

同様に， $\R^3$ を $\R$ 上のベクトル空間とみる。 $\boldsymbol{a}= (x,y,z)\in \R^3$ に対し，

\color{red}\lVert \boldsymbol{a}\rVert_2 = \sqrt{x^2+y^2+z^2}

と定めると，これもノルムになる。

高校では， $\vec{a}=(x,y)$ に対し，ベクトルの大きさ $|\vec{a}|=\sqrt{x^2+y^2}$ と定義したと思います。これは，例2で挙げたユークリッドノルムと同じものです。

より一般に，数ベクトル空間 $\R^n$ において， $\boldsymbol{a}=(a_1,a_2,\dots, a_n)\in\R^n$ に対し，

\color{red}\| \boldsymbol{a}\|_2 = \sqrt{a_1^2+a_2^2+\dots+a_n^2}

と定めると，これもノルムの定義を満たしていることがわかります。 $\mathbb{C}^n$ の場合は， $\boldsymbol{a}=(a_1,a_2,\dots, a_n)\in\mathbb{C}^n$ に対し，

\color{red}\| \boldsymbol{a}\|_2 = \sqrt{|a_1|^2+|a_2|^2+\dots+|a_n|^2}

と定義されます。

例3(絶対値ノルム・ $\ell^1$ ノルム).

$\R^2$ を $\R$ 上のベクトル空間とみる。 $\boldsymbol{a}= (x,y)\in \R^2$ に対し，

\color{red}\lVert \boldsymbol{a}\rVert_1 = |x|+|y|

と定めると，これはノルムになる。

同様に， $\R^3$ を $\R$ 上のベクトル空間とみる。 $\boldsymbol{a}= (x,y,z)\in \R^3$ に対し，

\color{red}\lVert \boldsymbol{a}\rVert_1 = |x|+|y|+|z|

と定めると，これもノルムになる。

例3も例1と同じような，絶対値ノルムの話です。例2と見比べてみてください。同じ $\R^2,\R^3$ という空間にもかかわらず，ノルムの定め方が違いますね。このように，同じベクトル空間でも，複数のノルムの定め方が可能です。

より一般に，数ベクトル空間 $\R^n$ において， $\boldsymbol{a}=(a_1,a_2,\dots, a_n)\in\R^n$ に対し，

\color{red}\| \boldsymbol{a}\|_1 = |a_1|+|a_2|+\dots+|a_n|

と定めると，これもノルムの定義を満たしていることがわかります。 $\mathbb{C}^n$ でも同じです。

もう一つ，代表的なノルムの定め方を紹介しましょう。

例4(最大値ノルム・ $\ell^\infty$ ノルム).

$\R^2$ を $\R$ 上のベクトル空間とみる。 $\boldsymbol{a}= (x,y)\in \R^2$ に対し，

\color{red}\lVert \boldsymbol{a}\rVert_\infty = \max\{ |x|,|y|\}

と定めると，これはノルムになる。実際，

$\lVert \boldsymbol{a}\rVert_\infty \ge 0$
$\lVert \boldsymbol{a}\rVert_\infty = 0\iff \boldsymbol{a}=\boldsymbol{0}$
$\lVert k\boldsymbol{a}\rVert_\infty =| k|\lVert\boldsymbol{a}\rVert_\infty$
$\lVert \boldsymbol{a}+\boldsymbol{b}\rVert_\infty\le \lVert \boldsymbol{a}\rVert_\infty +\lVert \boldsymbol{b}\rVert_\infty$

のうち，1,2,3.は明らかであり，4.については， $\boldsymbol{a}=(x,y),\; \boldsymbol{b}=(x',y')$ に対し，

\begin{aligned} \lVert \boldsymbol{a}+\boldsymbol{b} \rVert_\infty &= \max\{ |x+x'|, |y+y'|\}\\& \le \max\{ |x|+|x'|, |y|+|y'| \} \\&\le \max\{ |x|, |y|\} + \max\{ |x'| , |y'|\} \\& = \lVert \boldsymbol{a}\rVert_\infty+\lVert\boldsymbol{b} \rVert_\infty \end{aligned}

となるから，成り立っている。

同様に， $\R^3$ を $\R$ 上のベクトル空間とみる。 $\boldsymbol{a}= (x,y,z)\in \R^3$ に対し，

\color{red}\lVert \boldsymbol{a}\rVert_\infty = \max\{|x|,|y|,|z|\}

と定めると，これもノルムになる。

このノルムを最大値ノルムや $l^\infty$ ノルムといいます。

より一般に，数ベクトル空間 $\R^n$ において， $\boldsymbol{a}=(a_1,a_2,\dots, a_n)\in\R^n$ に対し，

\color{red}\| \boldsymbol{a}\|_\infty = \max\{ |a_1|,|a_2|,\dots,|a_n|\}

と定めると，これもノルムの定義を満たしていることがわかります。 $\mathbb{C}^n$ でも同じです。

さて，同じ空間でも複数のノルムの定め方があることを紹介しましたが，有限次元ベクトル空間においては，全てのノルムが同値であることが知られています。同値とは，収束の概念が同じということです。これについては，以下で解説しています。

ここでは，非常に簡単な例のみ紹介しました。より一般に， $L^p$ ノルムといわれるノルムは，関数解析でよく使われます。これについては，別の記事でいずれ解説しましょう。

ノルムはベクトル空間上に距離を定める

ノルムとは，ベクトル同士の「近さ」を定めるものです。

定理（ノルムは距離である）

ノルム空間 $V$ 上の関数 $d\colon V\times V \to [0,\infty)$ を

\color{red}d(\boldsymbol{x},\boldsymbol{y})= \lVert \boldsymbol{x}-\boldsymbol{y}\rVert

と定めると，これは距離関数となる。これにより，ノルム空間は距離空間となる。

距離関数・距離空間の復習をしておきましょう。

距離関数・距離空間

関数 $d\colon X \times X \to \mathbb{R}$ が以下の性質をみたすとき，距離関数 (distance function) という。

$d(x,y)\ge 0$
$d(x, y) = 0 \Longleftrightarrow x = y,$
$d(x, y) = d(y, x),$
$d(x,z) \le d(x, y) + d(y, z).$ （三角不等式）

このとき， $(X, d)$ ，または単に $X$ は距離空間 (metric space) であるという。

詳しくは距離空間の定義と6つの具体例～ユークリッド・マンハッタン距離～で解説しています。ノルムの定義と比較しましょう。ノルムの定義を再掲します。

ノルムの定義再掲

$\lVert \boldsymbol{x}\rVert \ge 0$
$\lVert \boldsymbol{x}\rVert = 0\iff \boldsymbol{x}=\boldsymbol{0}$
$\lVert k\boldsymbol{x}\rVert =| k|\lVert\boldsymbol{x}\rVert$ (斉次性)
$\lVert \boldsymbol{x}+\boldsymbol{y}\rVert\le \lVert \boldsymbol{x}\rVert +\lVert \boldsymbol{y}\rVert$ (三角不等式)

距離関数の定義1,2,4. はそれぞれノルムの定義1,2,4. から導けることがわかりますね。また，距離関数の定義3.については，ノルムの定義3.から