直交補空間の定義と性質9つ

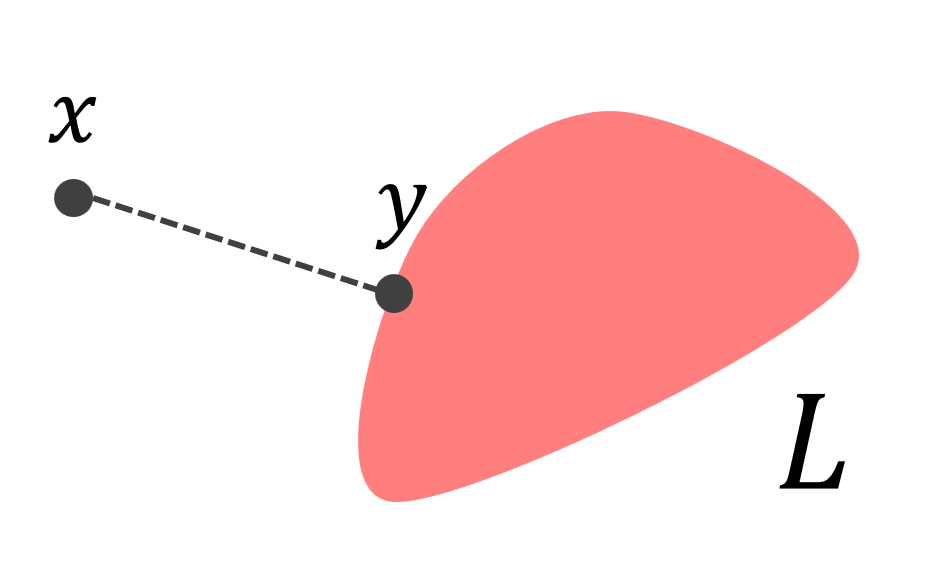
関数解析学の「内積空間」において，直交補空間とは，ある部分ベクトル空間とちょうど直交の関係になるベクトル全体の集合のことを指し，これもまたベクトル空間になります。

直交補空間について，その定義と性質とその証明を紹介しましょう。

直交補空間の定義
直交補空間の性質9つとその証明
関連する記事

直交補空間の定義

定義（直交補空間）

$X$ を内積空間とし， $A\subset X$ をその部分空間とする。このとき， $A$ の全てのベクトルと直交するようなベクトル全体の集合

\color{red} A^\perp = \{ x\in X\mid \langle x,a\rangle =0 ,\; \forall a\in A\}

を $A$ の直交補空間 (orthogonal complement) という。

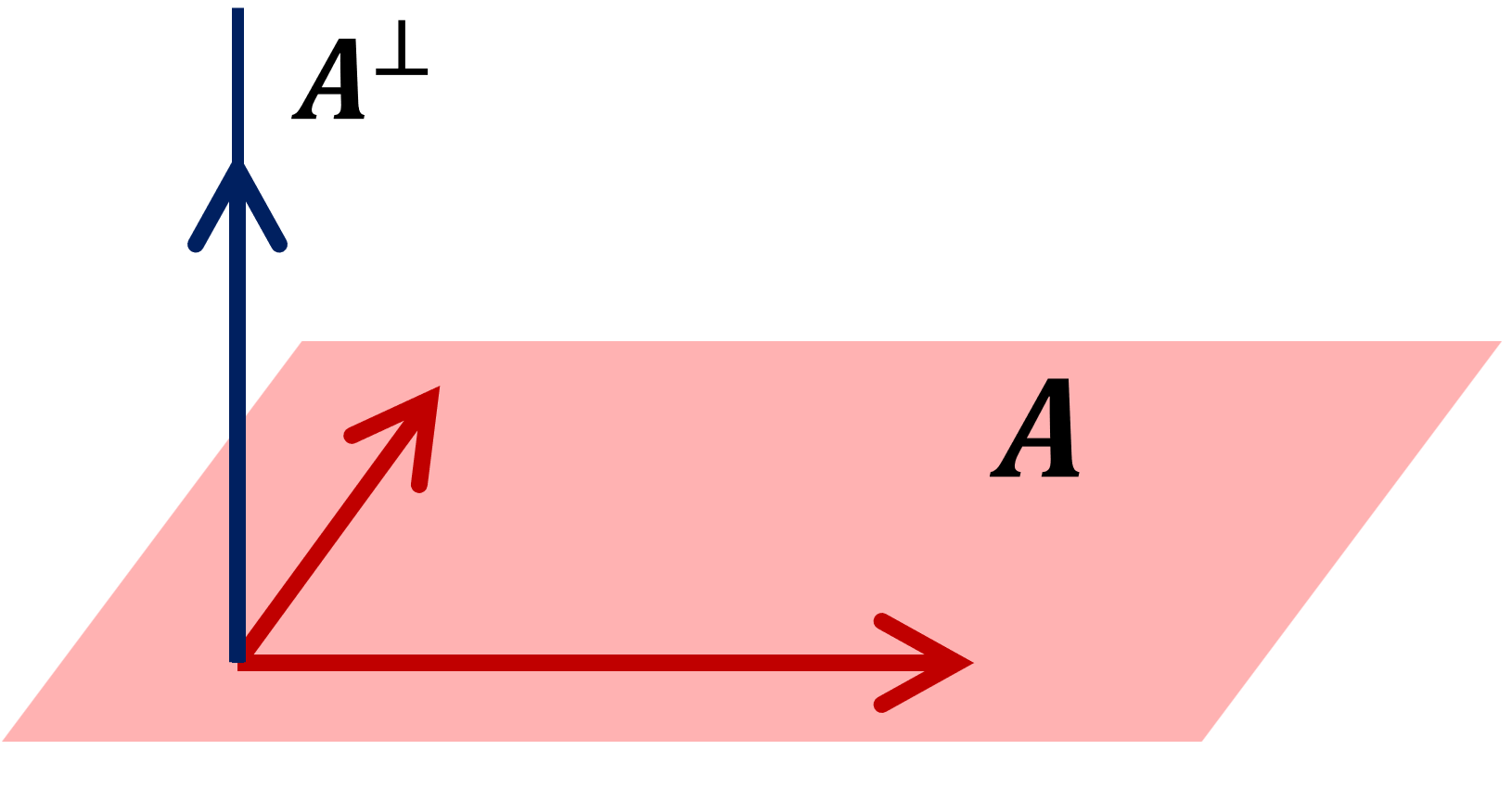
直交補空間は，ある部分空間 $A$ の全てのベクトルと直交するベクトル全体の集合だということですね。後の性質のところでも紹介しますが， $A^\perp$ は，それ自身が部分ベクトル空間になります。

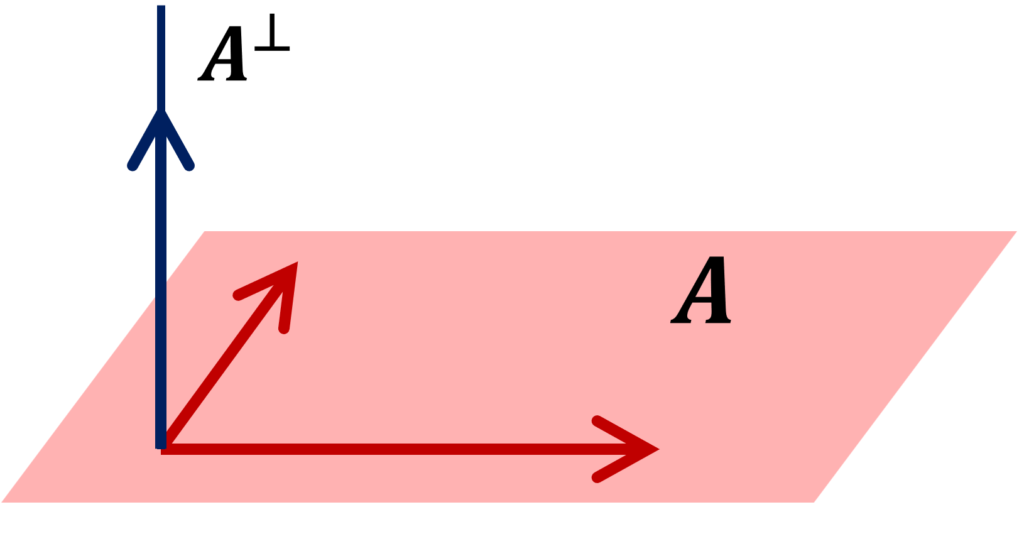
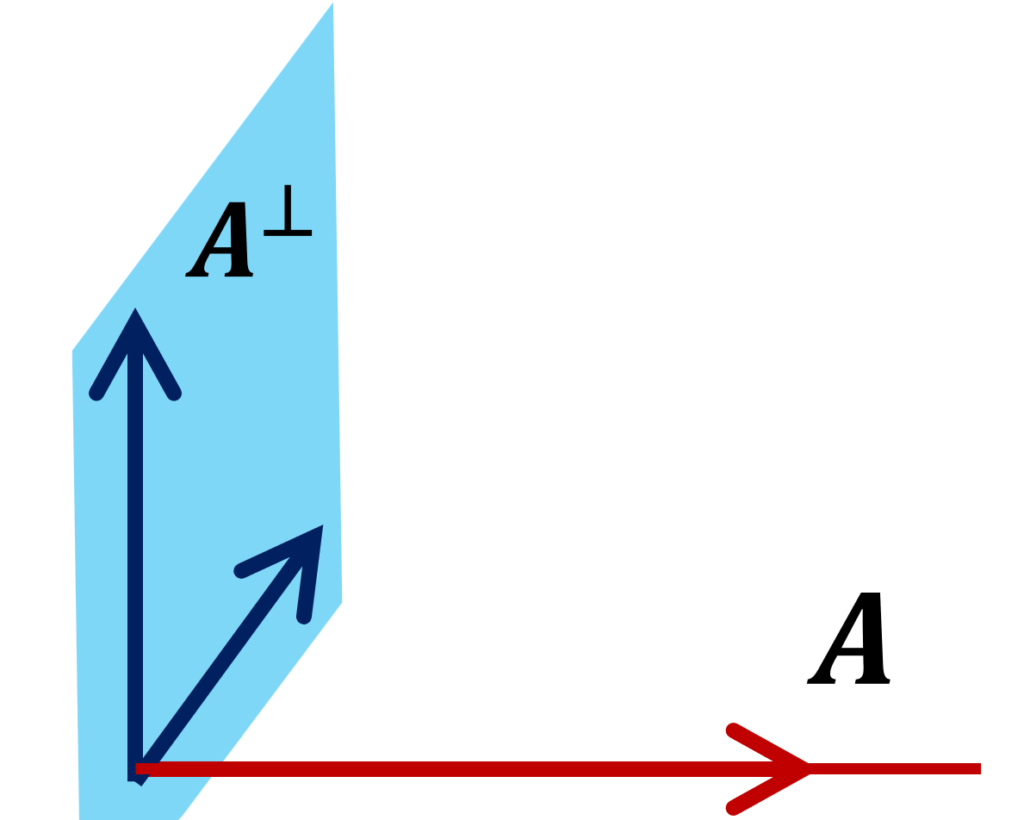
以下の図は3次元空間の場合の例です。実際は無限次元空間でも構いません。

直交補空間の性質9つとその証明

以下では，ヒルベルト空間における直交補空間の性質を述べます。ヒルベルト空間とは，完備な内積空間です(→ヒルベルト空間とは～定義・具体例・基本的性質～)。 $\overline{A}$ は $A$ の閉包を表すとします。

定理（直交補空間の性質）

$H$ をヒルベルト空間， $A,B\subset H$ をその部分空間とする。このとき，

$A^\perp$ は閉部分空間である。
$A\cap A^\perp =\{0\}$
$A\subset B\implies B^\perp \subset A^\perp$
$A^\perp = \bigl(\overline{A}\bigr)^\perp$
$A\subset (A^\perp)^\perp$
$\overline{A}=(A^\perp)^\perp$
$A$ が閉部分空間のとき， $H=A\oplus A^\perp$ である。すなわち，任意の $x\in H$ は $x=y+z \; (y\in A,\, z\in A^\perp)$ の形に一意的に分解できる(→ベクトル空間の直和)(射影定理)。
$(A+B)^\perp = A^\perp\cap B^\perp$ (→ベクトル空間の和)
$A,B$ が閉部分空間であるとき， $\overline{ A^\perp+B^\perp} = (A\cap B)^\perp$ (→ベクトル空間の和)

$A^\perp$ は $A$ の直交補空間と言われますが，それは7.があるからです。実際，一般のベクトル空間における「補空間」の概念は，直和を用いて定義されます。むしろ，7.が成り立つ状況のみで $A^\perp$ を直交補空間といい，そうでないときは $A^\perp$ は「直交補集合」など別の言い方をする流儀もあります。

1.～5.,8.は，単なる内積空間でも成立します。1.～9.を簡単に証明しておきましょう。

証明

1( $A^\perp$ は閉部分空間).について

$A^\perp$ が部分ベクトル空間であることは簡単な演習問題なので省略する。 $\{x_n\}\subset A^\perp$ とし， $x_n\to x\in H$ とする。このとき，任意の $a\in A$ に対し， $\langle x_n , a\rangle =0$ である。

内積の連続性(内積の記事の定理3)より， $\langle x_n , a\rangle\to \langle x , a\rangle$ が成立するため， $\langle x , a\rangle=0$ である。よって， $x\in A^\perp$ となるため， $A^\perp$ は閉である。

2( $A\cap A^\perp =\{0\}$ )について.

$x\in A\cap A^\perp$ とすると， $\langle x,x\rangle =0$ なので， $x=0$ である。

3( $A\subset B\implies B^\perp \subset A^\perp$ ).について

明らかに $\{ x\in X\mid \langle x,a\rangle =0 ,\; \forall a\in A\}\supset \{ x\in X\mid \langle x,a\rangle =0 ,\; \forall a\in B\}$ なので，示せた。

4( $A^\perp = \bigl(\overline{A}\bigr)^\perp$ ).について

$x\in A^\perp$ とする。 $a\in \overline{A}$ とすると， $\{a_n\}\subset A$ で $a_n\to a$ となるものが存在する。 $x$ の定義より， $\langle x,a_n\rangle = 0$ である。

一方で内積の連続性(内積の記事の定理3)より， $\langle x , a_n\rangle\to \langle x , a\rangle$ が成立するため， $\langle x , a\rangle=0$ である。よって， $x\in \bigl(\overline{A}\bigr)^\perp$ となる。

5( $A\subset (A^\perp)^\perp$ ).について

$x\in A$ とする。このとき，任意の $y\in A^\perp$ に対し， $y\perp A$ であるから，特に $\langle x,y\rangle =0$ である。これは， $x\in (A^\perp)^\perp$ を意味する。

6( $\overline{A}=(A^\perp)^\perp$ ).について

7.を用いる。7.より，