 確率論
確率論 マルコフの不等式とその証明をわかりやすく厳密に
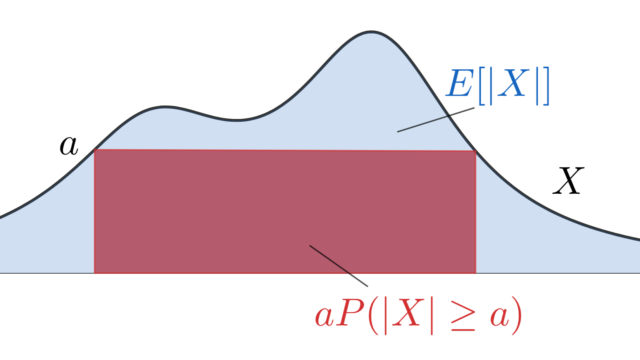
確率変数に対する不等式P(|X|≧a) ≦ E[|X|]/aをマルコフの不等式 (Markov's inequality) といいます。これについて,分かりやすくかつ厳密に証明しましょう。最後には,一般の測度論に関するマルコフの不等式を紹介します。
 確率論
確率論  LaTeX
LaTeX  数論
数論  確率論
確率論 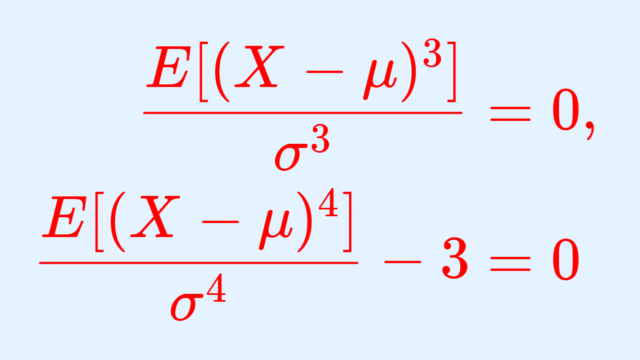 確率論
確率論 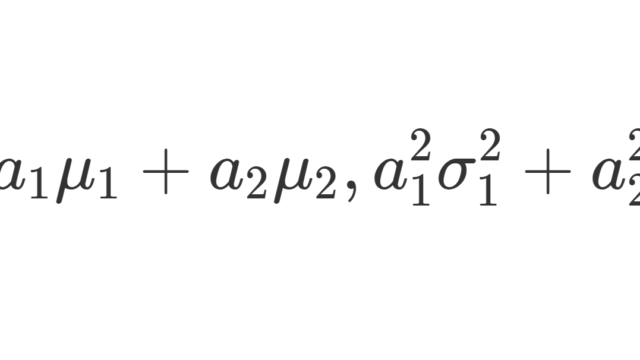 確率論
確率論 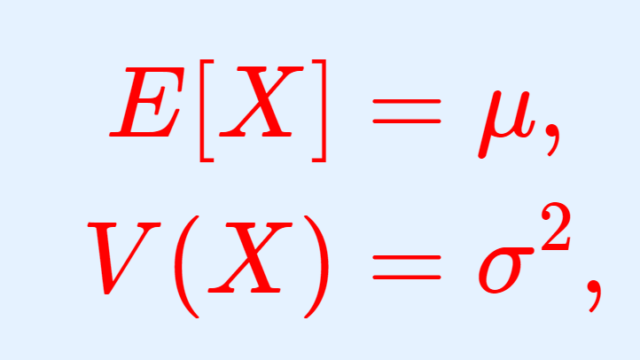 確率論
確率論 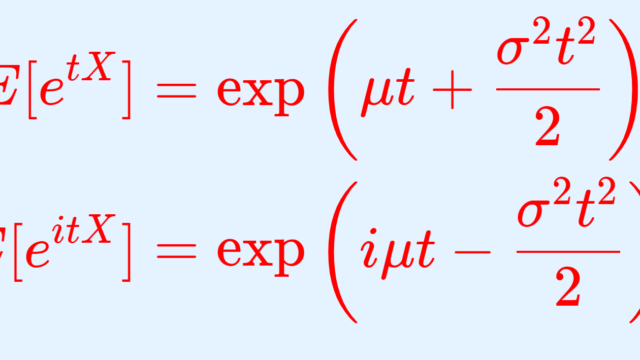 確率論
確率論  確率論
確率論 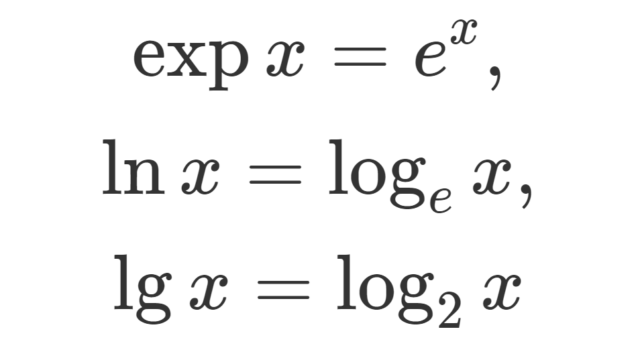 記号・記法
記号・記法