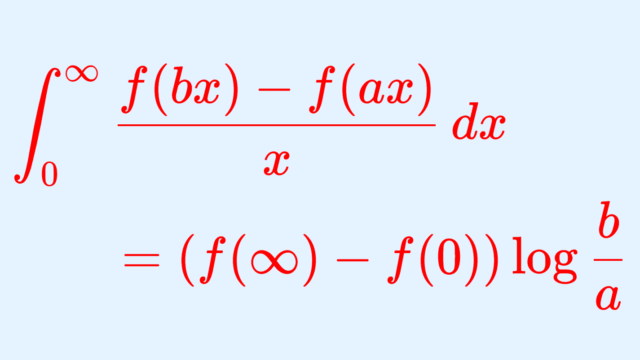 解析学(大学)その他
解析学(大学)その他 Frullani integralとその証明
Frullani 積分 (Frullani integral) について,その主張を紹介し,それを証明します。
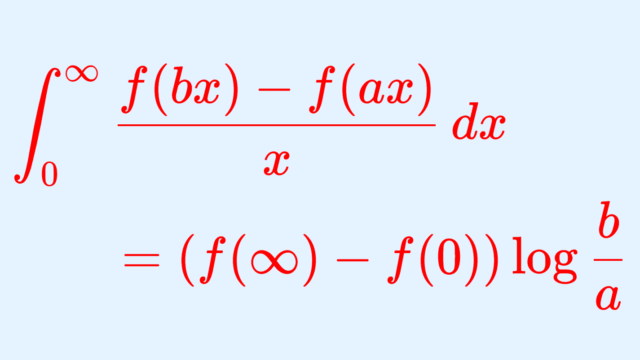 解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他  集合と位相
集合と位相  微分積分学(大学)
微分積分学(大学) 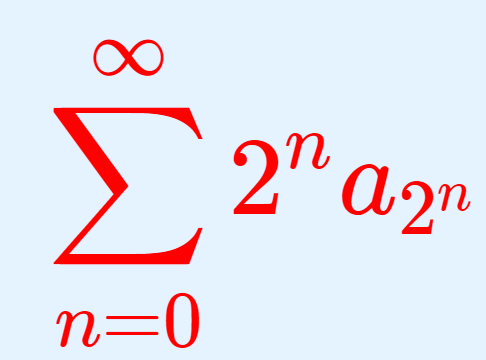 微分積分学(大学)
微分積分学(大学) 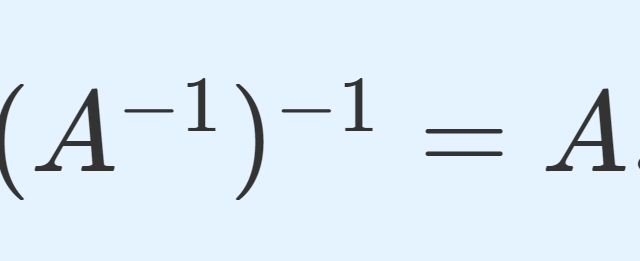 線形代数学
線形代数学  線形代数学
線形代数学 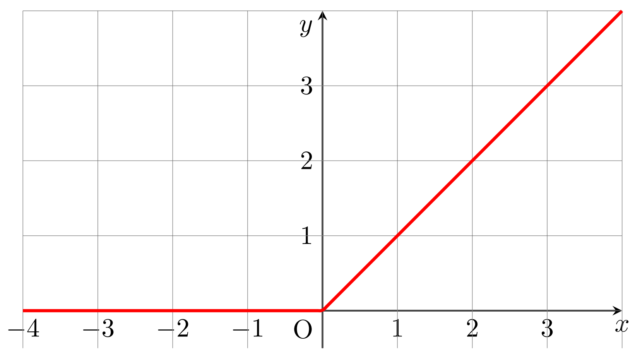 統計学
統計学 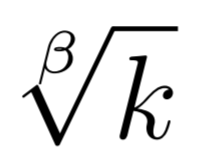 LaTeX
LaTeX  LaTeX
LaTeX