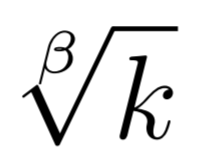 LaTeX
LaTeX 【LaTeX】ルート(根号)コマンドsqrtと高さ・位置の変更
LaTeXにおけるルート(根号,累乗根)のコマンド\sqrtと,\smashや\mathstruct,\vphantomを用いた高さ・深さの変え方,添え字の位置の変え方を説明します。なお,amsmath パッケージの使用は仮定しています。
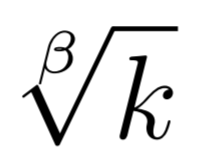 LaTeX
LaTeX  LaTeX
LaTeX  統計学
統計学 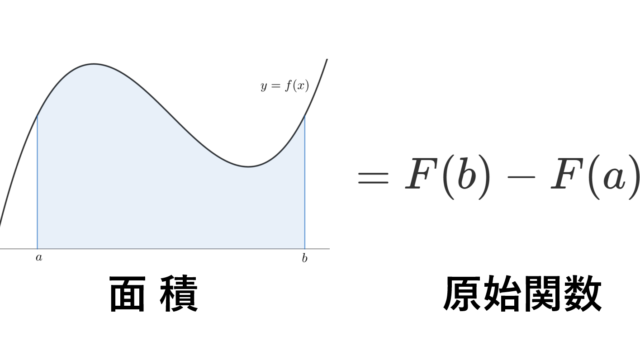 微分積分学(大学)
微分積分学(大学) 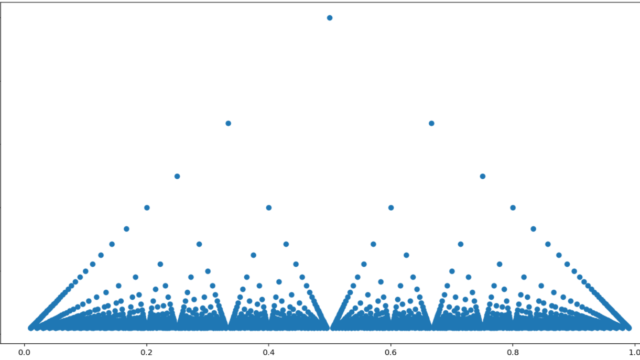 解析学(大学)その他
解析学(大学)その他 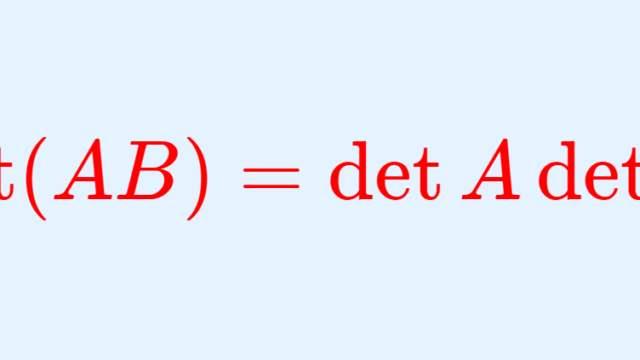 線形代数学
線形代数学 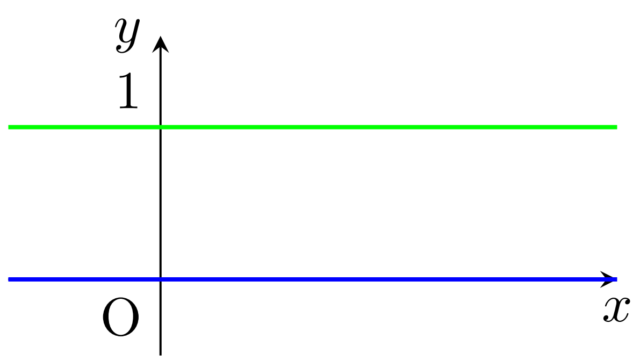 解析学(大学)その他
解析学(大学)その他 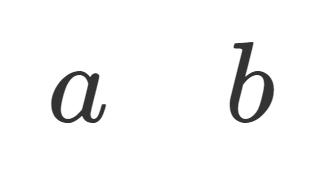 LaTeX
LaTeX 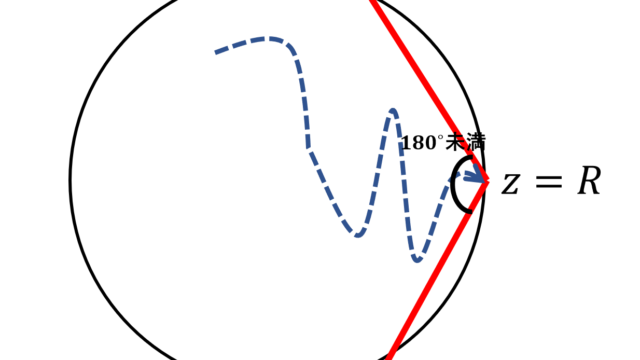 微分積分学(大学)
微分積分学(大学) 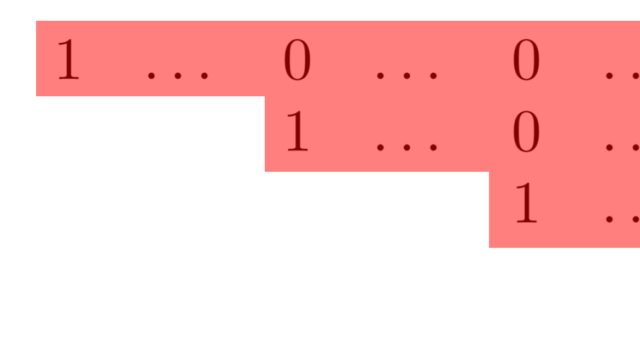 線形代数学
線形代数学