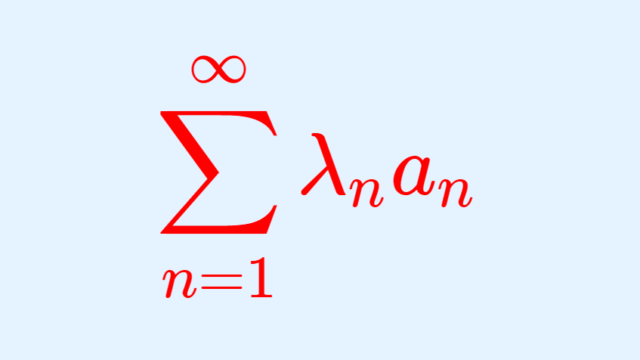 微分積分学(大学)
微分積分学(大学) 【級数の収束判定法】ディリクレの定理とその証明
ディリクレの収束判定法 (Dirichlet's test) またはディリクレの定理 (Dirichlet's theorem) といわれる,級数が収束する十分条件を紹介し,その証明を行います。そのために必要となる部分和分 (summation by parts) の証明も行います。
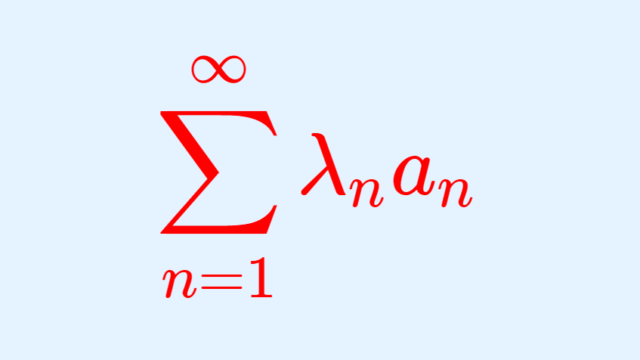 微分積分学(大学)
微分積分学(大学)  LaTeX
LaTeX  記号・記法
記号・記法 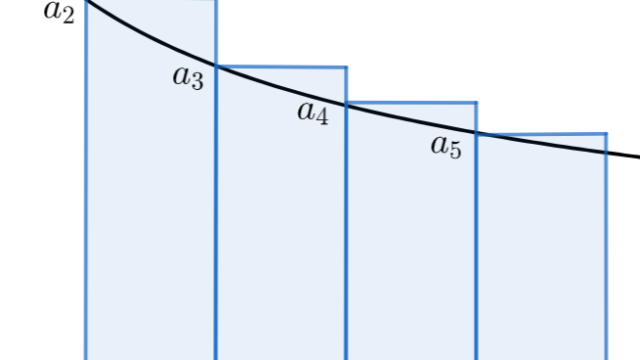 微分積分学(大学)
微分積分学(大学) 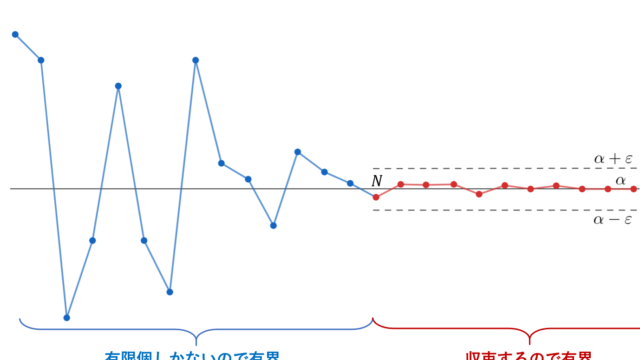 微分積分学(大学)
微分積分学(大学) 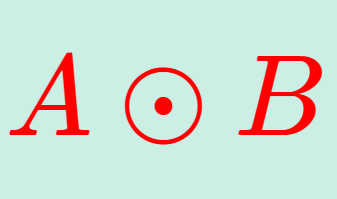 線形代数学
線形代数学 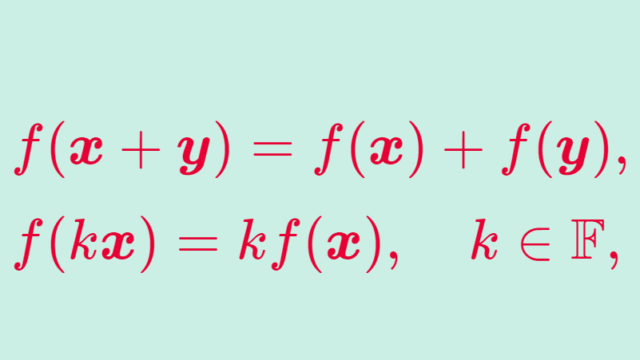 線形代数学
線形代数学 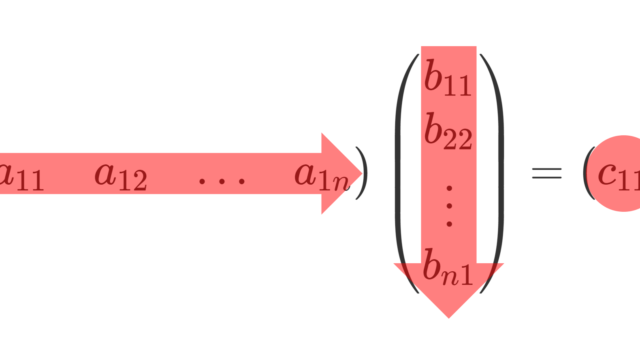 線形代数学
線形代数学 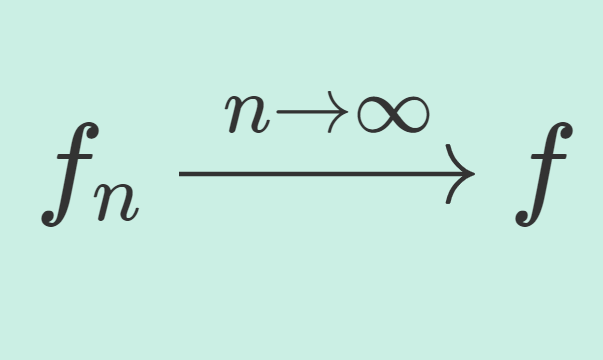 微分積分学(大学)
微分積分学(大学)  線形代数学
線形代数学