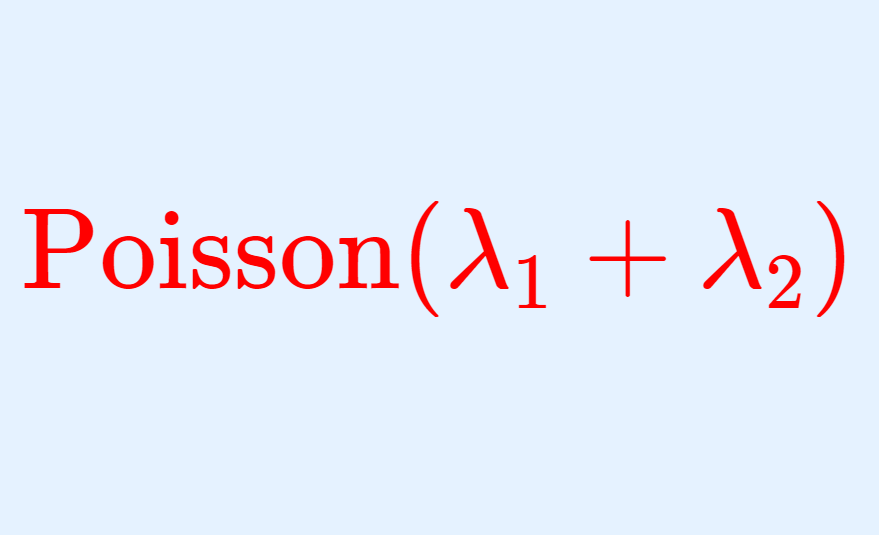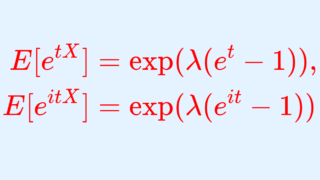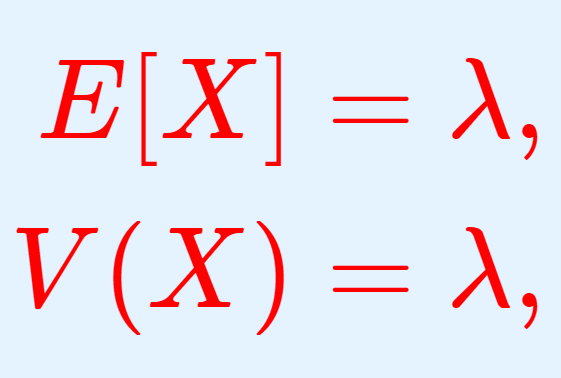ポアソン分布には,「再生性」と呼ばれる以下の性質があります。
\begin{aligned}&X_1\sim\operatorname{Poisson}(\lambda_1), X_2 \sim \operatorname{Poisson}(\lambda_2) \\ &\implies X_1+X_2\sim\operatorname{Poisson}(\lambda_1+\lambda_2) \end{aligned}
この性質について,その証明を,「定義から直接証明」「特性関数を用いた証明」の2通りで行いましょう。
ポアソン分布の再生性
まずは「再生性」の主張を正確に述べましょう。
定理(ポアソン分布の再生性)
\lambda_1, \lambda_2> 0 とし, X_1 \sim \operatorname{Poisson}(\lambda_1), \, X_2 \sim \operatorname{Poisson}(\lambda_2) を独立とする。このとき,
\color{red} X_1 + X_2 \sim \operatorname{Poisson}(\lambda_1+\lambda_2)
である。
同じ分布族の独立な確率変数を2つ足すと,また同じ分布族に属するとき,これを分布の再生性 (reproductive property) といいます。ポアソン分布や正規分布は,再生性をもつ分布として有名です。
さて,証明に入る前に,ポアソン分布の定義を軽く復習しておくことにします。
X を確率変数, \lambda > 0 とする。 k=0,1,2,\ldots に対し,
\color{red} P(X=k) = \frac{\lambda^k}{k!}e^{-\lambda }
が成り立つとき, X はパラメータ \lambda のポアソン分布 (Poisson distribution) に従うという。本記事では,これを \color{red}X\sim \operatorname{Poisson}(\lambda) とかくことにする。
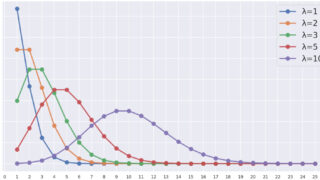
ポアソン分布は,「まれな事象が一定期間に起こる回数」をモデル化するのによく使います。詳しくは,以下の記事を参照してください。
ポアソン分布の再生性の証明
さて,ポアソン分布の再生性の証明をしていきましょう。
- 定義から直接証明する方法
- 特性関数を用いて証明する方法
の2通りを順番に紹介していきます。
【ポアソン分布の再生性】定義から直接証明
証明
k \ge 0 を整数とする。このとき, X_1, X_2 は独立なので,
\begin{aligned} &P(X_1+X_2= k) \\ &= \sum_{n=0}^k P(X_1 = n,\, X_2=k-n) \\ &= \sum_{n=0}^k P(X_1 = n)P( X_2=k-n) \\ &= \sum_{n=0}^k \frac{\lambda_1^n}{n!}e^{-\lambda_1 } \frac{\lambda_2^{n-k}}{(n-k)!}e^{-\lambda_2 } \\ &= \sum_{n=0}^k \frac{1}{n!(k-n)!} \lambda_1^n \lambda_2^{k-n} e^{-(\lambda_1+\lambda_2)} \end{aligned}
である。二項定理より,
なので,
より, P(X_1+X_2=k) = \frac{(\lambda_1+\lambda_2)^k}{k!}e^{-(\lambda_1+\lambda_2)} となるから, X_1+X_2\sim \operatorname{Poisson}(\lambda_1+\lambda_2) がわかる。
証明終
二項定理を用いることで,素直に証明することができましたね。
【ポアソン分布の再生性】特性関数を用いた証明
特性関数を用いた証明をする前に,ポアソン分布の特性関数を述べておきましょう。
これを踏まえると,以下のような証明が可能です。
証明
X_1, X_2 は独立であるから, E[e^{it(X_1+X_2)}] = E[e^{itX_1}]E[e^{itX_2}] なので,
\begin{aligned} &E[e^{it(X_1+X_2)}]\\&=\exp(\lambda_1(e^{it}-1)) \exp(\lambda_2(e^{it}-1)) \\ &=\exp((\lambda_1+\lambda_2)(e^{it}-1))\end{aligned}
であり,これはパラメータ \lambda_1+\lambda_2 となるポアソン分布の特性関数であるから, X_1+X_2\sim \operatorname{Poisson}(\lambda_1+\lambda_2) となる。
証明終
最後は,各分布とその特性関数は一対一に対応していることを使っています。特性関数が同じ確率変数は同分布だということです。
定義から直接証明するよりも,簡単に証明することができましたね。