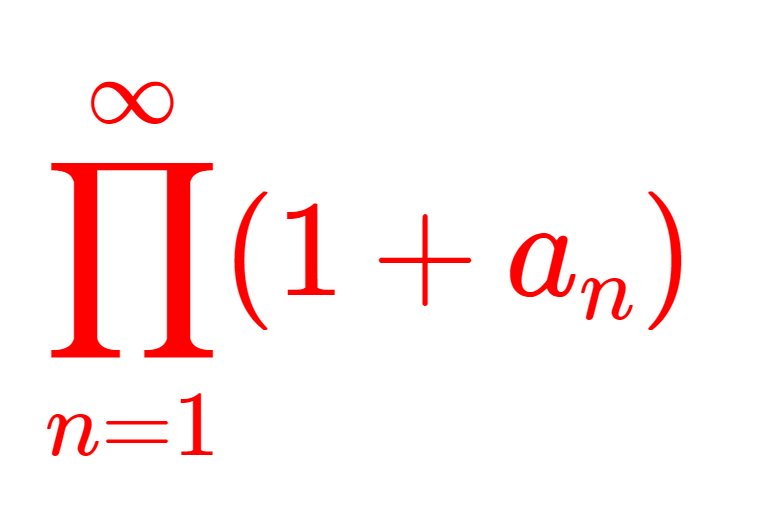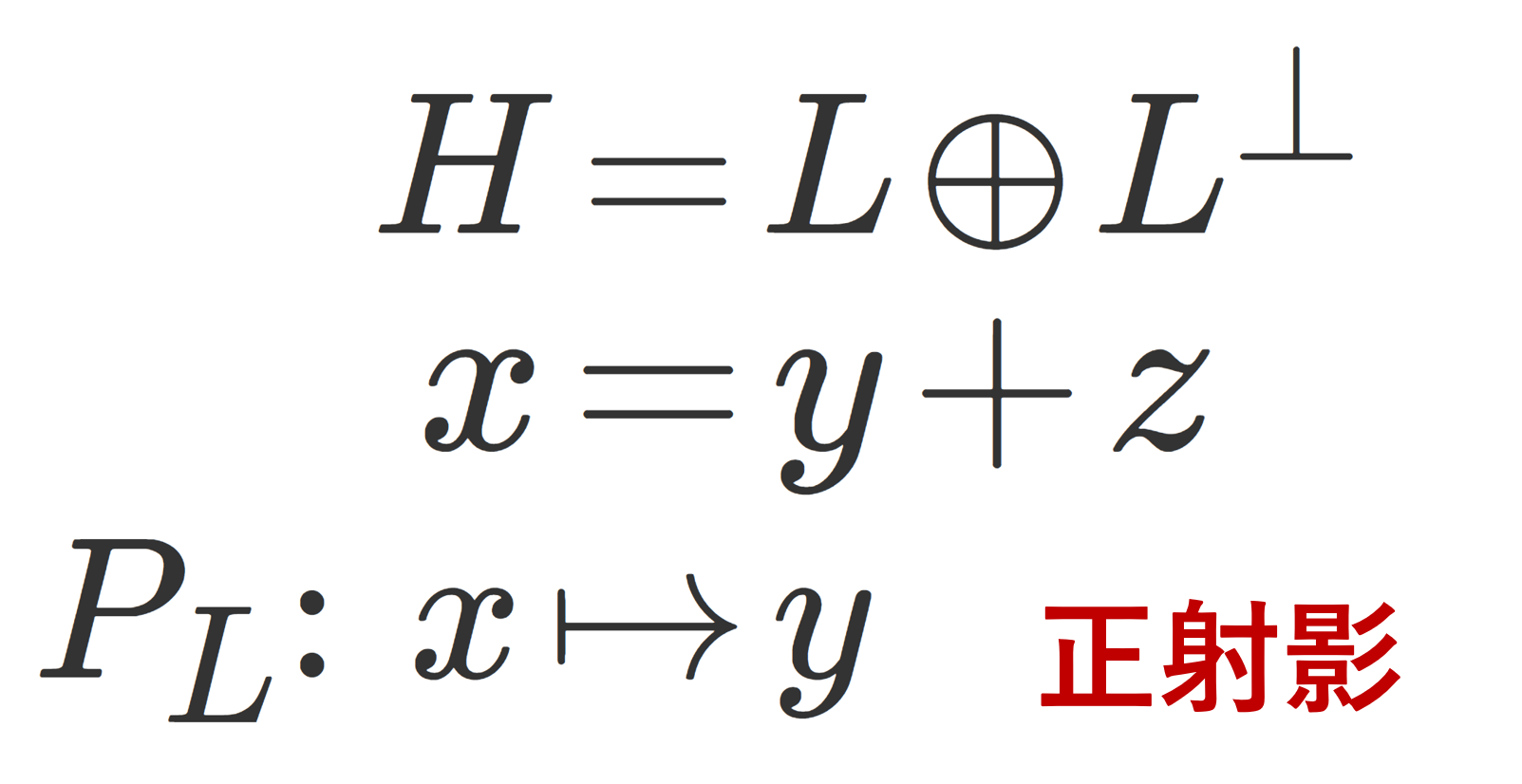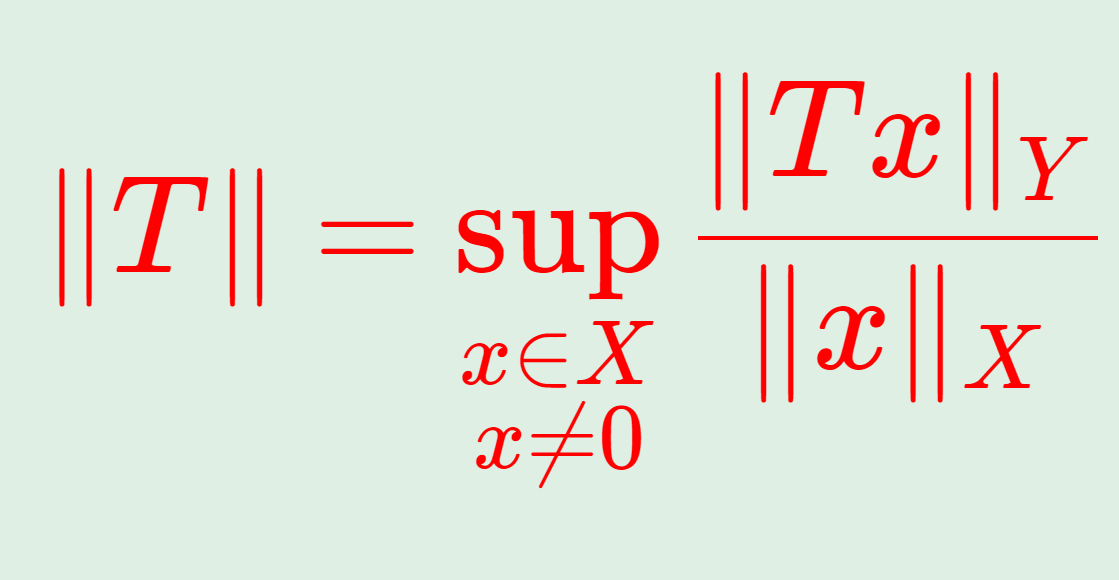無限積の定義と性質・無限和の収束との関係

無限積あるいは無限乗積とは，無限個の積 $\prod_{n=1}^\infty a_n = \lim_{N\to\infty} \prod_{n=1}^N a_n$ のことをいいます。無限積の定義と，その収束性について，無限和との関連性や絶対収束を含めて述べましょう。

無限積の収束の定義
無限積の基本的な性質
無限和との関係と無限積の絶対収束
無限積の定義の一般化

無限積の収束の定義

和を $\sum$ (シグマ)記号で表すのと同様に，積は $\prod$ (パイ)記号を用いて，

\color{red}a_1\times a_2\times \dots \times a_n =\prod_{k=1}^n a_k

と表すのが普通です。これにおいて， $n\to\infty$ を考えます。

定義1（無限積・無限乗積）

$\prod_{k=1}^n a_k$ が $n\to\infty$ のときに $0$ でない値に収束するとき，無限積(無限乗積)は収束する (converge) といい， $\color{red} \prod_{n=1}^\infty a_n$ と表す。

$\{a_n\}$ は複素数列で良いです。

収束値は $0$ でないとしています。これは， $0$ を許すと， $a_n=0$ となるものが1つでもあると他の項の値に関係なく収束してしまうので，面白くないし，逆に厄介だからです。

また， $a_n=0$ となるものがなければ OK かというとそうでもありません。たとえば定数列 $a_n=1/2$ を無限個かけると $0$ になりますが，これを「無限積が収束する」というと，以下の定理1が成り立ちません。

無限積の基本的な性質

定理1（無限積の各項の収束）

$\prod_{n=1}^\infty a_n$ が収束する必要十分条件は，

\begin{equation}\color{red}\lim_{m,n\to\infty} \prod_{k=m}^n a_k =1\end{equation}

となることである。また $(1)$ 式より特に，無限積が収束するならば $\color{red} \lim_{n\to\infty} a_n =1$ である。

コーシー列に近い話ですね。ちなみに，無限積の収束の定義に $0$ を許すと，この定理は成立しません。 $\lim_{m,n\to\infty} \prod_{k=m}^n a_k =1$ とは，任意の $\varepsilon >0$ に対して，ある $N\ge 1$ が存在して，

n\ge m\ge N \implies \left| \prod_{k=m}^n a_k -1\right| <\varepsilon

の意味です。特に，上で $n\to\infty$ とすると， $\left| \prod_{k=m}^\infty a_k -1\right| \le \varepsilon$ ですから，定理の $\impliedby$ 方向( $(1)$ ならば収束方向)はほぼ明らかです。

定理1の $\implies$ の証明

$P_n=\prod_{k=1}^n a_k$ と定めると， $\lim_{m,n\to\infty} \prod_{k=m}^n a_k =P_n/P_m$ である。無限積の収束先を $P(\ne 0)$ とすると，

\lim_{m,n\to\infty} \frac{P_n}{P_m} =\frac{P}{P}=1

である。特に， $a_n = P_n/P_{n-1} \xrightarrow{n\to\infty}1$ である。

証明終

このことから，無限積の収束は， $a_n$ を $1+a_n$ に置き換えて，

\large\color{red}\prod_{n=1}^\infty (1+a_n)

の形で考えることが多いです。こうすれば， $\lim_{n\to\infty}a_n =0$ となります。以降は，この形で考えることにしましょう。

無限和との関係と無限積の絶対収束

数列の各項は $a_n >-1$ をみたすとしましょう。 $\prod_{k=1}^n (1+a_k)$ で対数を取ると，

\log \prod_{k=1}^n (1+a_k) =\sum_{k=1}^n \log (1+a_k)

となります。無限積が収束するとき， $n\to\infty$ とすると， $\sum_{k=1}^\infty \log (1+a_k)$ は収束し，逆に $\sum_{k=1}^\infty \log (1+a_k)$ が収束するとき，

\prod_{k=1}^n (1+a_k) =\exp\left(\sum_{k=1}^n \log (1+a_k)\right)

ですから，無限積も収束することが分かります。したがって，以下の定理が成立します。

定理2（無限積と無限和の収束）

$a_n>-1$ とする。

$\prod_{n=1}^\infty (1+a_n)$ が収束する必要十分条件は $\sum_{n=1}^\infty \log (1+a_n)$ が収束することである。

$a_n>-1$ としましたが，対数の枝をはっきり定めておけば， $\{a_n\}$ を複素数にしても同じです。

定理2の和の形を応用して，無限積に対しても絶対収束を定義します。

定義2（無限積の絶対収束）

$a_n>-1$ とする。

\sum_{n=1}^\infty \log(1+a_n)

が絶対収束するとき，無限積 $\prod_{n=1}^\infty (1+a_n)$ は絶対収束 (absolutely converge) するという。

定理2と上の定義より，明らかに無限積が絶対収束すれば収束します。

無限積の絶対収束については，以下の性質が成り立つことが知られています。

定理3（絶対収束と無限和の同値条件）

$a_n>-1$ とするとき，以下の3つは同値である。

$\color{red}\displaystyle \prod_{n=1}^\infty (1+|a_n|) <\infty$
$\color{red}\displaystyle \sum_{n=1}^\infty |\log(1+a_n)|<\infty$
$\color{red}\displaystyle \sum_{n=1}^\infty |a_n|<\infty$

$a_n>-1$ としましたが，対数の枝をはっきり定めておけば， $\{a_n\}$ を複素数にしても同じです。

1. は $\prod_{n=1}^\infty (1+|a_n|)$ が収束すると言っています。 $1+|a_n| \ge 1$ ですから，単に「 $<\infty$ 」というだけで収束すると言えるわけですね。2. は $\prod_{n=1}^\infty (1+a_n)$ が絶対収束することの定義ですが，同値性により，1.から3.のどれを絶対収束の定義にしても構いません。書籍によって定義が異なることがあります。

この定理により， $\prod_{n=1}^\infty (1+a_n)$ が絶対収束することの判定には，単に $\sum_{n=1}^\infty |a_n|<\infty$ を見ればよいということが分かりますね。

定理3の証明

2. $\iff$ 3.について

2, 3のどちらか一方を仮定すると， $a_n \xrightarrow{n\to\infty} 0$ である。ここで， $\lim_{x\to 0} \log (1+x)/x = 1$ であるから，特に $\lim_{x\to 0} |\log (1+x)/x| = 1$ である。したがって，任意の $\varepsilon >0$ に対して，十分大きな $n$ で

(1-\varepsilon) |a_n| \le |\log(1+a_n)|\le (1+\varepsilon )|a_n|

が成り立つ。これにより示せた。

1. $\iff$ 2.について

2. $\iff$ 3.より， $\sum_{n=1}^\infty |\log(1+a_n)|<\infty\iff \sum_{n=1}^\infty |a_n|<\infty\iff \sum_{n=1}^\infty \log(1+|a_n|)<\infty$ である。定理2.より，最後は $\prod_{n=1}^\infty (1+|a_n|)$ が収束することと同値である。従って示せた。

証明終

注意ですが，以上は絶対収束の話であり， $\sum_{n=1}^\infty a_n$ の収束は， $\prod_{n=1}^\infty (1+a_n)$ の収束のための必要条件でも十分条件でもないです。以下に例を挙げておきます。

無限和の条件収束と無限積の条件収束が一致しない例

$\color{red}a_1=0,\, a_{2n}=\frac{1}{\sqrt{n}}, \, a_{2n+1} = -\frac{1}{\sqrt{n}+1}$ のとき， $\prod_{n=1}^\infty (1+a_n)$ は収束するが， $\sum_{n=1}^\infty a_n$ は収束しない。
$\color{red} a_{n}=\frac{(-1)^{n+1}}{\sqrt{n}}$ のとき， $\prod_{n=1}^\infty (1+a_n)$ は収束しないが， $\sum_{n=1}^\infty a_n$ は収束する。

例の証明

1.について

$(1+\frac{1}{\sqrt{n}})(1-\frac{1}{\sqrt{n}+1})=1$ なので，無限積は $1$ に収束する。一方で， $a_{2n}+a_{2n+1}=\frac{1}{\sqrt{n}(\sqrt{n}+1)}\ge \frac{1}{2n}$ より，無限和は収束しない。

2.について

無限和の収束は交代級数の収束性の証明とその具体例より良い。

\lim_{n\to\infty} \frac{a_n-\log(1+a_n)}{a_n^2}=\frac{1}{2}

であるから，十分大きい $n$ に対して，

a_n -\log(1+a_n)> \frac{1}{4} a_n^2

とできる。この両辺無限和を取ることを考える。 $\sum_{n=1}^\infty a_n$ が収束することと， $\sum_{n=1}^\infty a_n^2=\sum_{n=1}^\infty 1/n =\infty$ であることから， $\sum_{n=1}^\infty \log(1+a_n) =-\infty$ にならねばならない。定理2より， $\sum_{n=1}^\infty a_n$ は発散する( $0$ に発散する)。