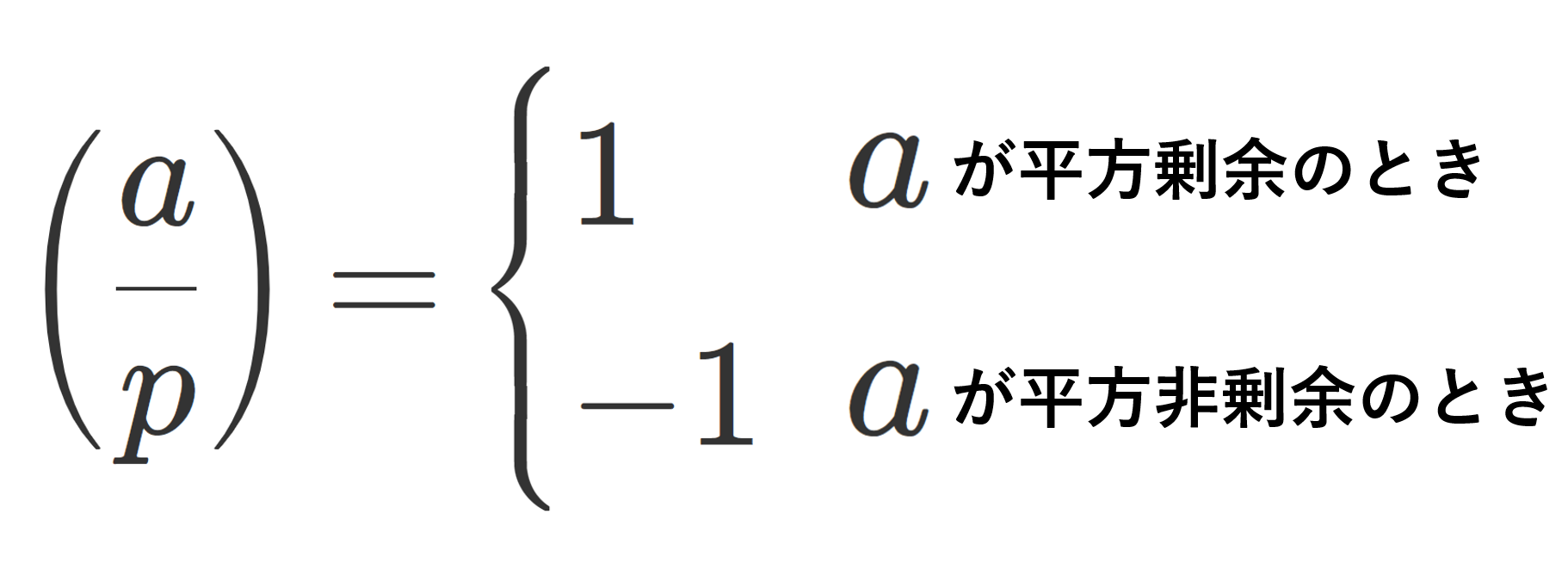合同式における平方剰余・平方非剰余の概念と,それを扱うのに便利なルジャンドル記号の定義・性質について,順を追って解説していきましょう。
平方剰余・平方非剰余
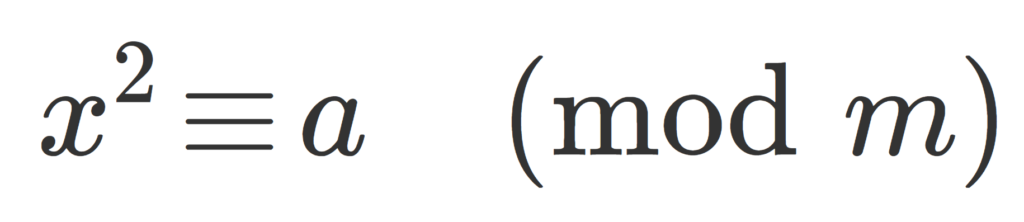
平方剰余・平方非剰余の定義
定義(平方剰余・平方非剰余)
m を正の整数, a を整数とする。
\Large\color{red} x^2\equiv a \pmod m
となる整数 x が存在するとき, a を,m を法とする平方剰余 (quadratic residue)であるといい,そうでないとき平方非剰余 (quadratic nonresidue) であるという。
2 乗の形で表したのと合同になるものが平方剰余なわけですね。
例を挙げましょう。
例1.
{}\bmod{}5 において, 0^2\equiv 0,\, (\pm1)^2\equiv 1,\, (\pm2)^2\equiv 4 であるから, 0,1,4 は平方剰余, 2,3 は平方非剰余である。
例2.
{}\bmod{}8 において, 0^2\equiv 0,\, (\pm1)^2\equiv 1,\, (\pm2)^2\equiv 4,\, (\pm3)^2\equiv 1,\, 4^2\equiv 0 であるから, 0,1,4 は平方剰余, 2,3,5,6,7 は平方非剰余である。
0,1 は常に平方剰余です。
平方剰余・平方非剰余の個数
定理1(平方剰余の個数)
m\ge 3 を整数とするとき,0,1,2,\dots, m-1 のうち {}\bmod m で平方剰余であるものの個数は高々 \left\lfloor\dfrac{m+2}{2} \right\rfloor 個である( \lfloor\cdot \rfloor は床関数(ガウス記号))。
特に m=p が奇素数であるとき, 0,1,2,\dots, p-1 のうちで平方剰余の個数はちょうど \dfrac{p+1}{2} 個である。
奇素数とは奇数の素数,すなわち 3 以上の素数のことです。
証明を記載しておきます。
証明
前半について
m が奇数のとき,整数は 0,\pm 1,\pm 2 ,\dots, \pm (m-1)/2 のどれかと合同であるから,平方剰余は 0, 1^2, 2^2, \dots, ((m-1)/2)^2 のいずれかと合同である。 よって平方剰余は高々 (m+1)/2 個である。
m が偶数のとき,整数は 0,\pm 1,\pm 2, \dots, \pm(m/2-1) , m/2 のどれかと合同であるから,平方剰余は 0,1^2, 2^2, \dots, (m/2)^2 のいずれかと合同である。よって平方剰余は高々 (m+2)/2 個である。
後半について
平方剰余は 0, 1^2, 2^2, \dots, ((p-1)/2)^2 のいずれかと合同であるが,これらが互いに合同でないことを示せばよい。 x^2\equiv y^2 とすると,
(x+y)(x-y)\equiv 0 \pmod p
であり,よって x+y \equiv 0 または x-y\equiv 0 である。 x,y\in\{ 0,1,2,\dots, (p-1)/2\} とすると, x=y である。故に, 0, 1^2, 2^2, \dots,((p-1)/2)^2 は互いに合同でない。よって題意は示された。
証明終
ルジャンドル記号
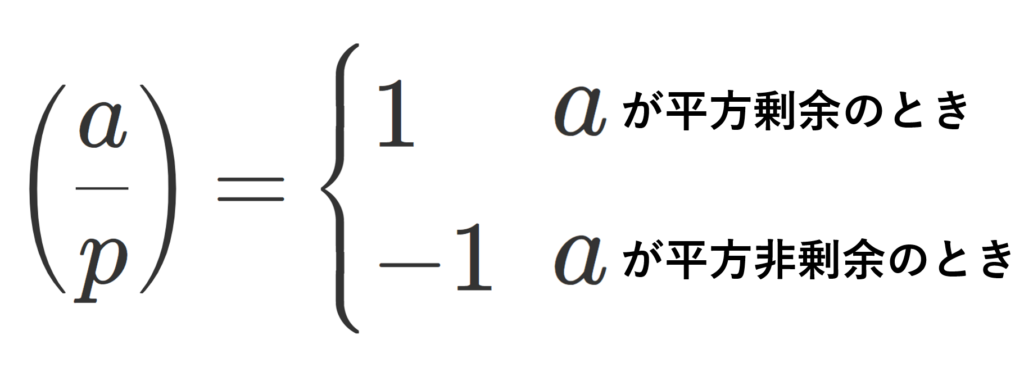
平方剰余・平方非剰余を扱うのに便利なのが「ルジャンドル記号」です。ルジャンドル記号について,解説しましょう。
ルジャンドル記号の定義
定義(ルジャンドル記号)
p を奇素数とする。 \mod p に関して a\not\equiv 0 が平方剰余のとき,
\large\color{red}\left( \frac{a}{p} \right) = 1
とし,平方非剰余のとき,
と定める。これをルジャンドル記号 (Legendre symbol) という。
単に平方剰余のとき 1,平方非剰余のとき -1 にしているだけですね。便利記号です。 a\equiv a' ならば当然 \left( \dfrac{a}{p} \right) = \left( \dfrac{a'}{p} \right) です。
a\not\equiv 0 としましたが, a\equiv 0 ならば \displaystyle \left( \frac{a}{p} \right) = 0 と定義することがあります。この方が,あとの性質との整合性が取れて良いからです。
ルジャンドル記号は,p が奇素数の場合しか考えません。これでは不便なので,奇素数でないものに拡張した「ヤコビ記号」というものがありますが,本記事では省略します。
例3.
p=7 のとき, 1^2\equiv 1,\, 2^2\equiv 4,\,3^2\equiv 2,\, 4^2\equiv 2,\, 5^2\equiv 4,\, 6^2\equiv 1 であるから, 1,2,4 は平方剰余で, 3,5,6 は平方非剰余である。これより,
\begin{aligned}\left(\frac{1}{7}\right)&= \left(\frac{2}{7}\right)= \left(\frac{4}{7}\right)=1,\\ \left(\frac{3}{7}\right) &= \left(\frac{5}{7}\right) = \left(\frac{6}{7}\right) =-1 \end{aligned}
である。
ルジャンドル記号の性質(オイラーの判定法)
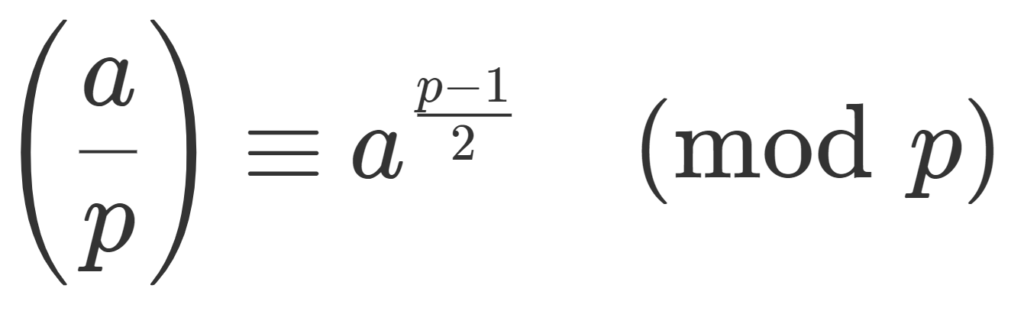
ルジャンドル記号の性質とは,そのまま平方剰余・平方非剰余の性質になります。
定理(ルジャンドル記号の性質(オイラーの判定法))
p は奇素数,a,b はどちらも p と互いに素とする。このとき,
- \displaystyle\color{red} \left(\frac{a}{p}\right) \equiv a^{\frac{p-1}{2}}\pmod p.
- \displaystyle\color{red} \left( \frac{ab}{p}\right) = \left( \frac{a}{p}\right) \left( \frac{b}{p}\right).
1.は, a が平方剰余かどうかの判定は,単に a^{\frac{p-1}{2}} を {}\bmod p で考えればよいと言っています。例1,2では,平方剰余かどうかの判定に 0^2, (\pm1)^2, (\pm2)^2, \dots, (\pm\frac{p-1}{2})^2 を全部計算していましたが,その必要はないわけです。
証明
1. \displaystyle\color{red} \left(\frac{a}{p}\right) \equiv a^{\frac{p-1}{2}}\pmod p について
a が平方剰余であるとする。x^2\equiv a\pmod p とすると,フェルマーの小定理より,
a^{\frac{p-1}{2}}\equiv x^{p-1} \equiv 1=\left(\frac{a}{p}\right)
である。次に a が平方非剰余とする。
x=1,2,\dots, p-1 に対して, xx^* \equiv a となる x^* が 1,2,\dots, p-1 の中にただ一つ存在する。 a は平方非剰余なので,常に x\not\equiv x^* である。よって, 1,2,\dots, p-1 を xx^*\equiv a となる (p-1)/2 個のペア (x,x^*) に分けることができる。したがって,
(p-1)! \equiv a^{\frac{p-1}{2}} \pmod p
である。一方でウィルソンの定理 (p-1)!\equiv -1 から,
となる。
2. \displaystyle\color{red} \left( \frac{ab}{p}\right) = \left( \frac{a}{p}\right) \left( \frac{b}{p}\right) について
1.より,
\left(\frac{ab}{p}\right) \equiv (ab)^{\frac{p-1}{2}} = a^{\frac{p-1}{2}} b^{\frac{p-1}{2}} \equiv \left(\frac{a}{p}\right) \left(\frac{b}{p}\right).証明終
ルジャンドル記号のその他の性質
定理(平方剰余の相互法則)
p,q を奇素数とする。このとき,
- \displaystyle \color{red}\left(\frac{-1}{p}\right) =(-1)^{\frac{p-1}{2}}.
- \displaystyle \color{red}\left(\frac{2}{p}\right) =(-1)^{\frac{p^2-1}{8}}.
- \displaystyle \color{red}\left(\frac{q}{p}\right) \left(\frac{p}{q}\right) =(-1)^{\frac{p-1}{2}\cdot\frac{q-1}{2}}.
この証明は,別の記事で行うことにしましょう。