集合の「濃度」とは,集合の要素の個数の概念を,無限個の集合についても適用できるよう一般化したものです。これの定義について,分かりやすく丁寧に説明していきましょう。
集合の濃度のアイデアから厳密な定義へ
集合の濃度について,まずはその定義のアイデアを述べ,それから厳密な定義につなげましょう。
有限個の集合の大小は数を知らない赤ちゃんでもわかる
有限個の集合の大小を考えるとき,我々はどうするでしょうか。以下を見てください。

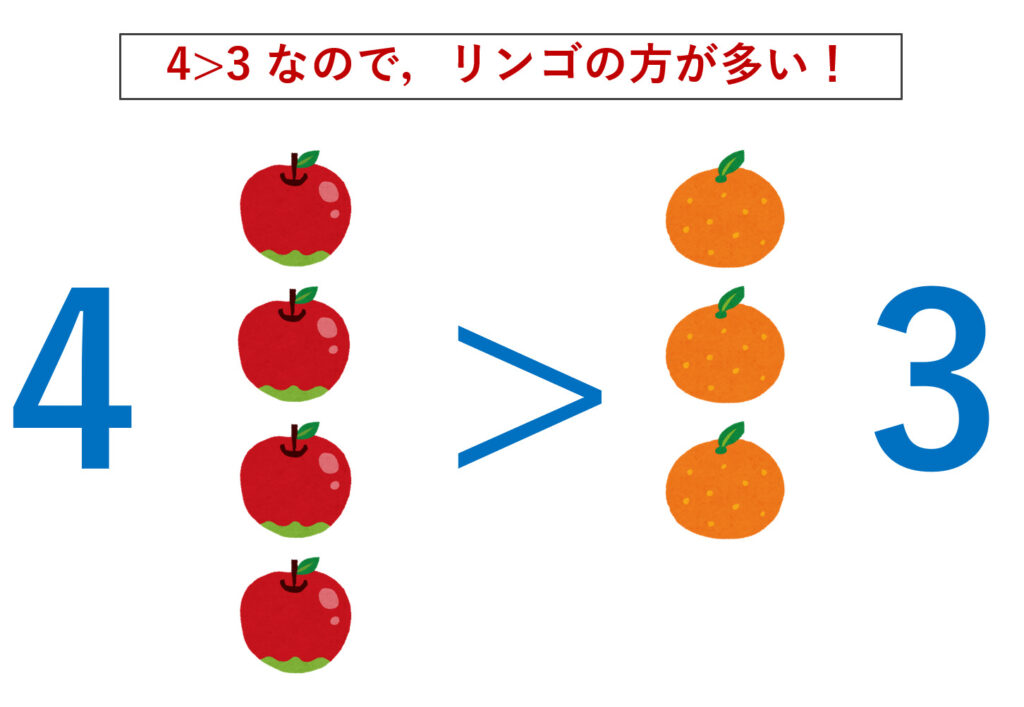
リンゴとミカンの数はどちらの方が多いでしょうか。
我々は「数」を知っているので,以下のように数を考えて,大きさを比較するでしょう。
しかし,赤ちゃんの場合はどうでしょうか。赤ちゃんは「数」を知りません。「数」を知らなくても,リンゴとミカンの数の大小が分かるでしょうか。
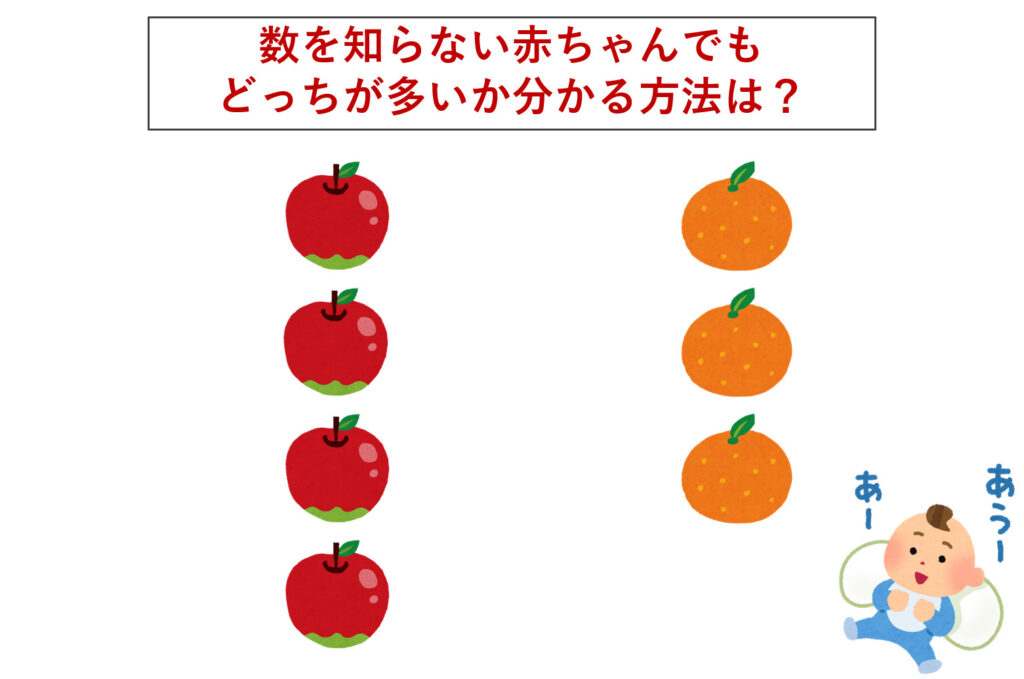
我々は「数」を知っているが故に,逆に難しく感じるかもしれません。結論を言うと,「数」を知らなくても,以下のように,「ペア」を作ってあげることで,どちらの方が多いか考えることができますね。
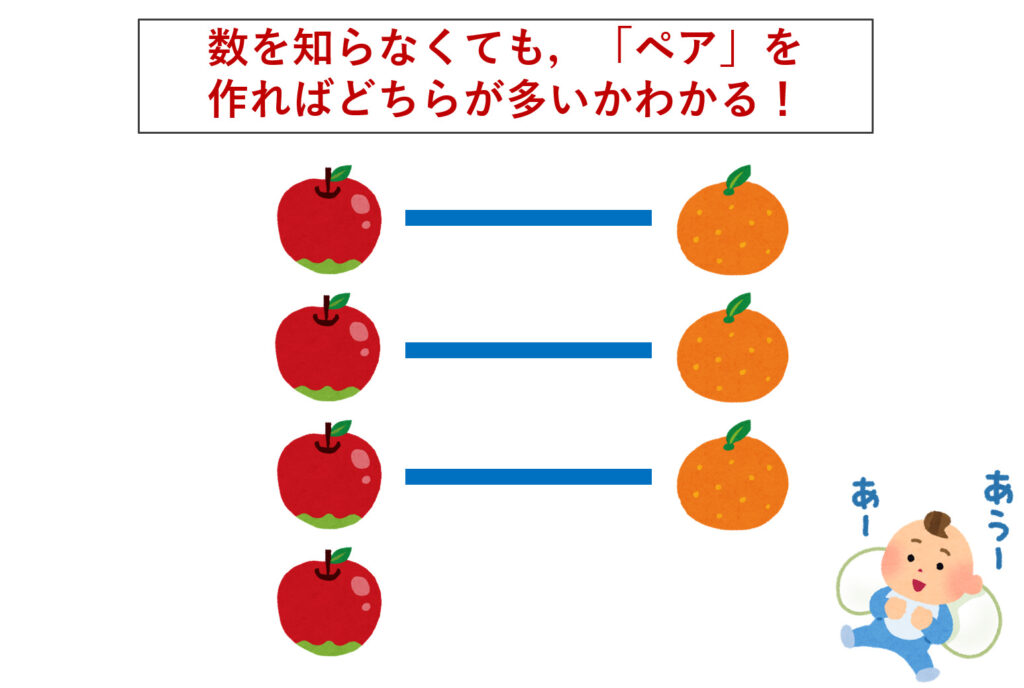
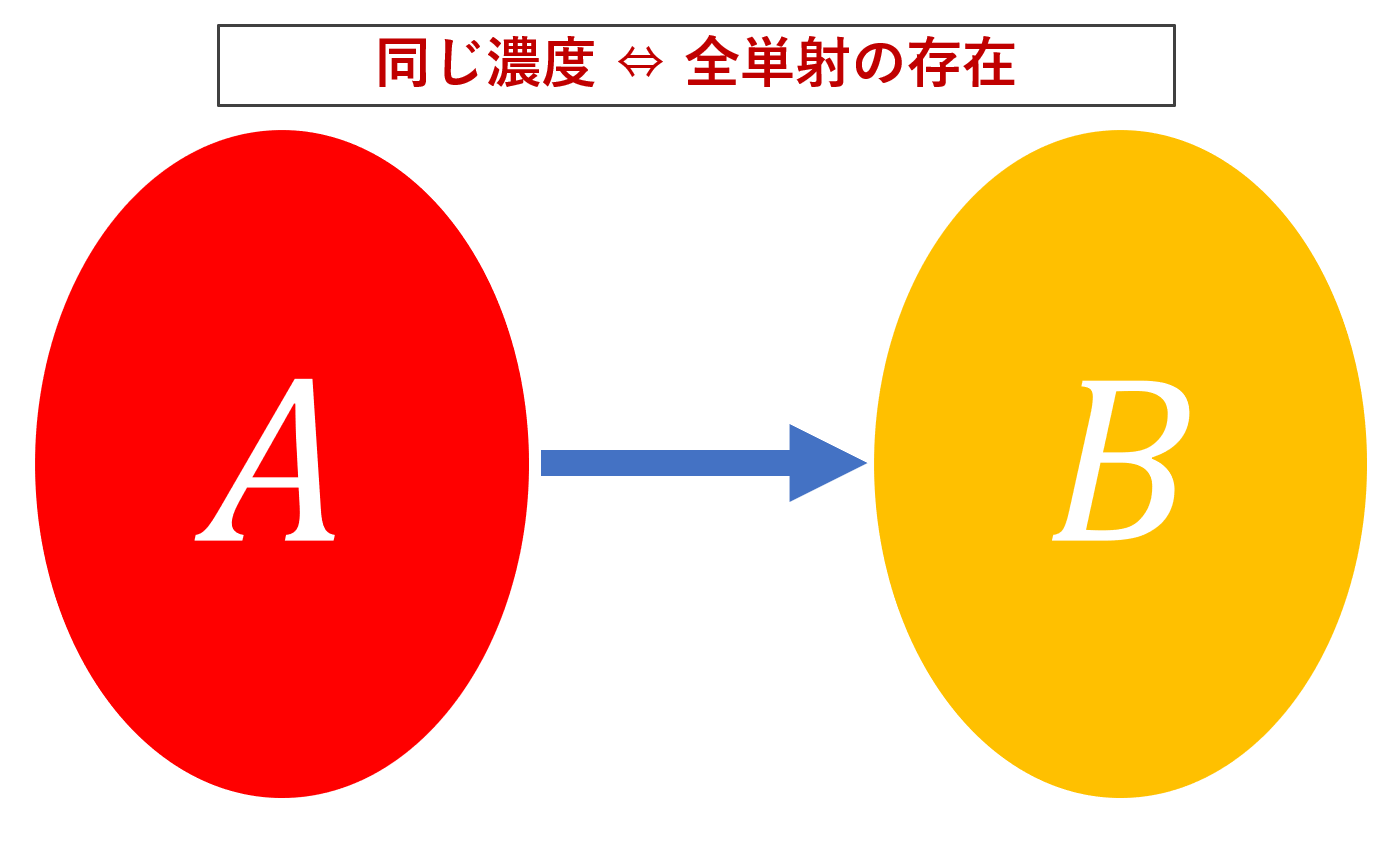
「ペア」とは,対応関係のことで,数学の言葉で言えば,写像のことです。両者が同じ数かどうかは,2つの集合の間に全単射が作れるかで判断できます。
まとめると,数の概念を知らずとも,集合間で「ペア」を作って「あまり」が出ないかどうか,すなわち,写像の言葉でいうと,全単射が存在するかどうかで,集合の大小が判断できるわけですね。
無限個の集合にも数の大小をつけたい!
無限個の場合は,我々も数を数えることができません。しかし,上と同じように考えれば,数の大小を考えることができそうですね。これが,集合の濃度のアイデアです。厳密な定義を述べましょう。
集合の濃度の厳密な定義
定義(集合の濃度)
A,B を集合とする。
- 全単射 f\colon A\to B が存在するとき,\color{red} |A|=|B| とかき, A , B の濃度 (cardinality) は等しいという。
- 単射 f\colon A \to B が存在するとき, \color{red} |A| \le |B| とかき, A の濃度 (cardinality) は B の濃度以下であるという。
- 上で,単射は存在するが,全単射が存在しないとき, \color{red}|A| < |B| とかき, A の濃度 (cardinality) は B の濃度未満であるという。
- A が要素が n 個の有限集合であるとき, \color{red} |A| = n とかき,濃度は n であるという。
A の濃度は \color{red} |A| の他,\color{red} \#A や \color{red} \operatorname{Card}(A) ともかくことがある。
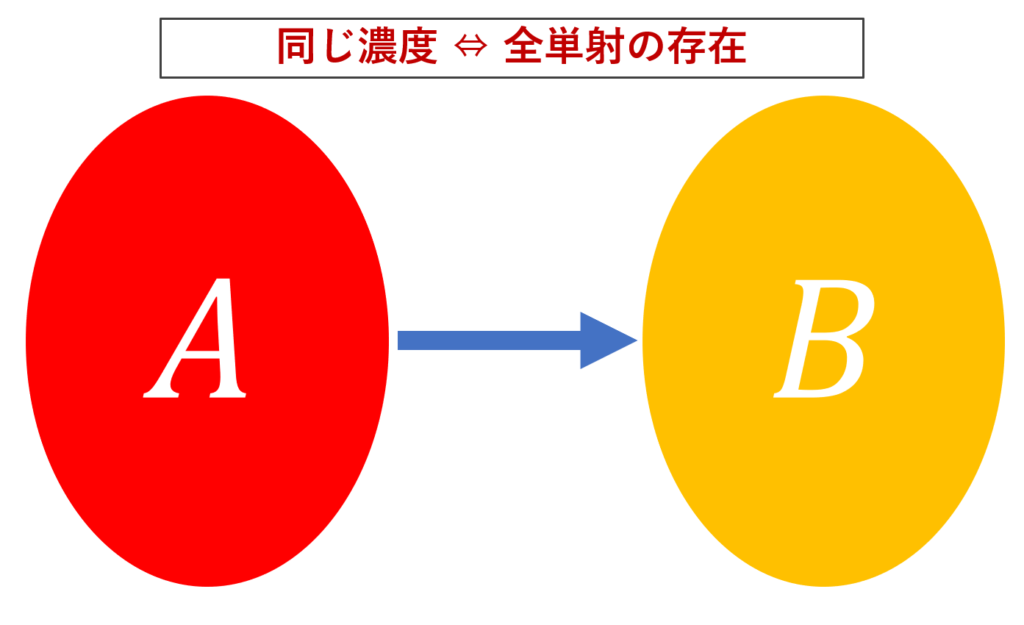
濃度は「集合の個数」の概念を一般化したものです。有限個のときは,単に集合の個数と同じで,無限個のときは,単射の存在性によって大小を定めています。
注意ですが,濃度が等しいというためには,全単射は一つでも存在すればよいです。これについての具体例は,後で述べることにしましょう。
ここで,以下のことがらは明らかです。
実際,集合の濃度における = は「全単射の存在」を意味していますから,確認可能ですね。また,
- |A|\le |B|,\; |B|\le |C| \implies |A|\le |C|
も分かります。さらに,次の定理が知られています。
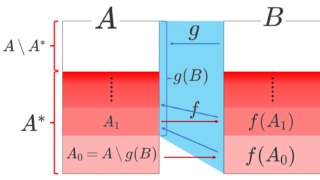
ベルンシュタインの定理
|A| \le |B| かつ |B|\le |A| ならば, |A|=|B| である。
これは,記号 \le が,ちゃんと順序関係を表している(全順序集合となる)ことを示しています(関連記事:半順序集合・全順序集合の定義・具体例4つとその周辺)。
日本語で言うと,単射 f\colon A\to B,\,\, g\colon B\to A が存在すれば,全単射 h\colon A\to B が必ず存在するということですね。
これの証明は以下にあります。
集合の濃度の具体例
具体例を挙げましょう。注意ですが,濃度が等しいとは,全単射が一つでも存在すれば良いんでした。
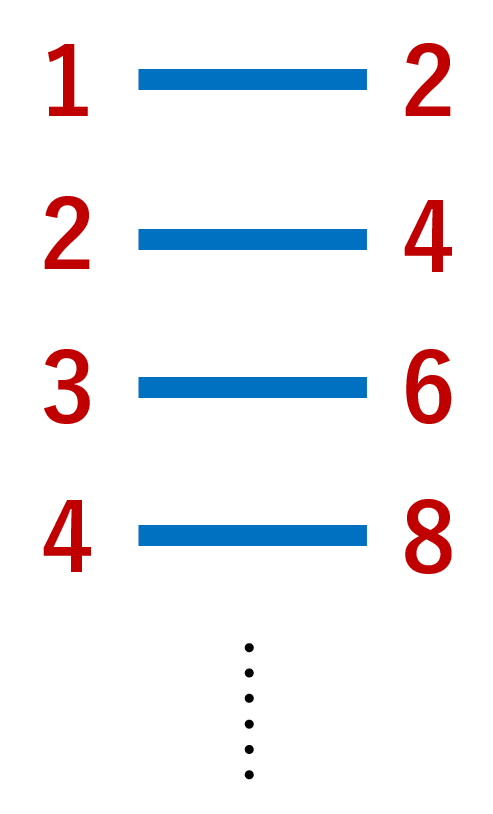
例1.
\mathbb{N} =\{ 1,2,3,\ldots\},\; 2\mathbb{N}=\{2,4,6,\ldots\} (正の整数全体の集合と正の2の倍数全体の集合) とする。このとき,
\color{red} |\mathbb{N}| = |2\mathbb{N}|
である。
集合の包含としては, 2\mathbb{N} \subsetneq \mathbb{N} ですから,これは若干受け入れ難いかもしれません。ただ,たとえば, f(n) = 2n という写像を考えると,確かに f\colon \mathbb{N} \to 2\mathbb{N} は全単射になっていますから,両者の濃度が等しいといえるわけです。
例2.
\color{red}|(0, 1)| = |\mathbb{R}|
である。
これも (0,1)\subsetneq \mathbb{R} ですから,少々驚くかもしれませんが,たとえば, f(x) = \tan (\pi x-\pi/2) とすると, f\colon (0,1)\to \mathbb{R} が全単射になりますから,濃度は等しくなります。
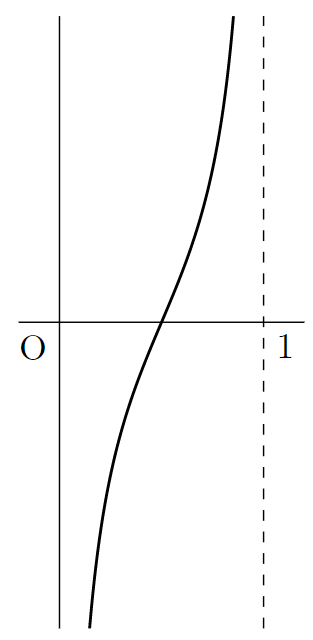
もう一つだけ例を挙げましょう。
例3.
\color{red} |[0,1] | = |(0,1)|
である。
これは,たとえば
f(x) = \begin{cases} 1/2 & x=0, \\ 1/2^{k+2} & x = 1/2^k\; (k=0,1,2,\ldots), \\ x & \text{otherwise} \end{cases}
とすると, f\colon [0,1]\to(0,1) は全単射になります。
可算集合・非可算集合(可算無限・非可算無限)
集合の濃度の定義をもとに,正の整数の集合 \mathbb{N} と同じ濃度をもつものや,それより大きい濃度を持つものを考えることが可能です。これらは,それぞれ可算集合 (countable set)・非可算集合 (uncountable set) といいます。また,どちらも「無限個」なわけですが,その無限を区別して,可算無限・非可算無限という言葉もあります。
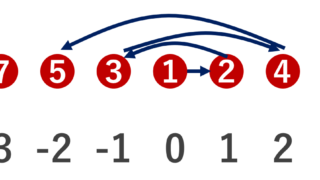
例1.で挙げましたが, |2\mathbb{N}| = |\mathbb{N}| ですから, 2\mathbb{N} は可算集合です。また,整数全体の集合 \mathbb{Z} や,有理数全体の集合 \mathbb{Q} も可算集合であることが分かっています。
一方で, \mathbb{R} や (0,1) は非可算無限です。
これらについて詳しくは,以下の記事で解説しましょう。