さまざまな分野で登場するシグモイド関数について,その定義とグラフ,性質をまとめます。
シグモイド関数の定義
定義(シグモイド関数)
a>0 とする。このとき,
\color{red} f_a(x) = \frac{1}{1+e^{-ax}}=\frac{e^{ax}}{e^{ax}+1}
をシグモイド関数 (sigmoid function) という。とくに, a=1 のとき,標準シグモイド関数 (standerd sigmoid function) という。
シグモイド関数は,統計学における累積分布関数や,機械学習におけるニューラルネットワークの活性化関数でもよく登場する関数です。(ほかに,生物の神経細胞が持つ性質をモデル化したものでもあるようです。)
この関数について,深く掘り下げていきましょう。
シグモイド関数のグラフ
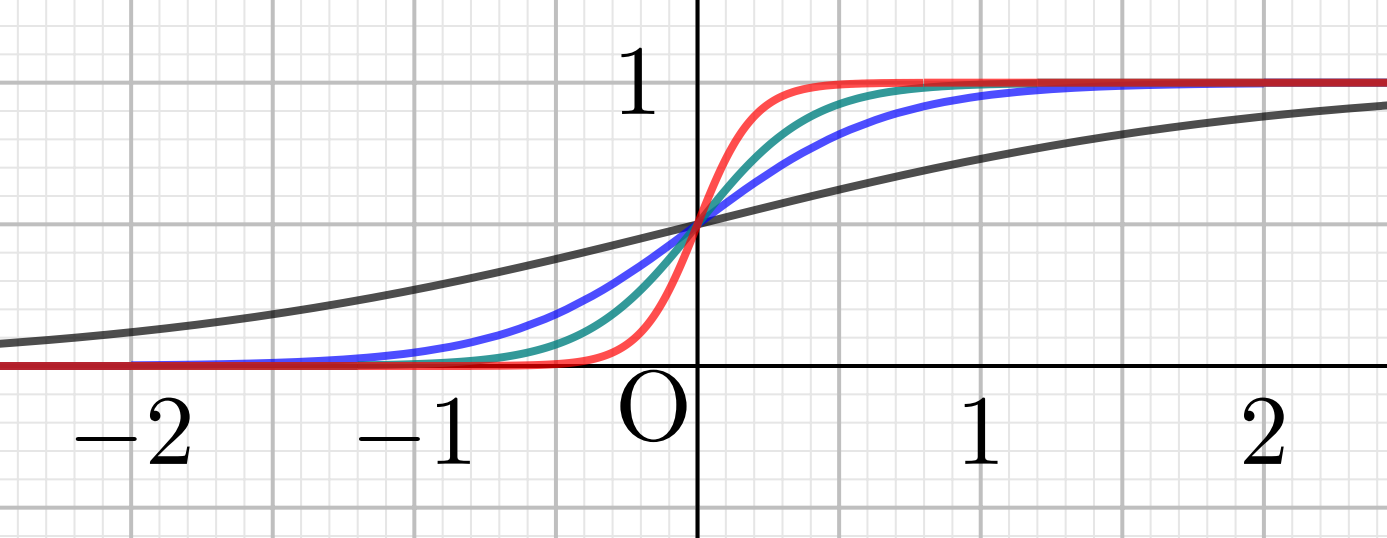
シグモイド関数のグラフは,以下のようになります。黒・青・緑・赤の順に, a=1, 3, 5, 10 としています。
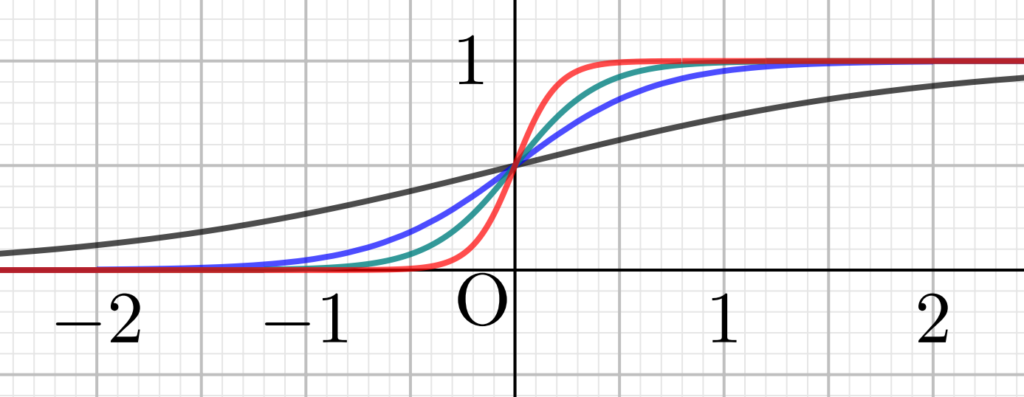
シグモイド関数の性質
定理(シグモイド関数の性質)
f_a をシグモイド関数とするとき,
- f_a は狭義単調増加である。
- f_a は (0,1/2) に関して対称である。また,この点は唯一の変曲点である。
- \displaystyle \lim_{x\to -\infty} f_a(x) = 0, \quad \lim_{x\to\infty} f_a(x) = 1.
- \displaystyle f_a'(x) =a f_a(x)(1-f_a(x)).
- f_a は C^\infty 級,すなわち無限回微分可能である。
- f_a は双曲線関数 \tanh を用いて, f_a(x) =\frac{1+\tanh(ax/2)}{2} とも表せる。
- \displaystyle f_a^{-1} (x) = \frac{1}{a}\log \frac{x}{1-x} \quad (0<x<1). (逆関数)
- \displaystyle \lim_{a\to\infty} f_a(x) = \begin{cases} 1 & 0<x, \\ 1/2 & x=0,\\ 0 & x< 0. \end{cases}
ここでは,性質2, 4, 6, 7, 8 について詳しく確認することにしましょう。
2. シグモイド関数が(0,1/2)に関して対称であること
証明
\begin{aligned} f_a(x)+f_a(-x)&= \frac{1}{1+e^{-ax}}+\frac{1}{1+e^{ax}} \\ &= \frac{(1+e^{ax})+(1+e^{-ax})}{(1+e^{-ax})(1+e^{ax})} \\ &= 1 \end{aligned}
であるから,特に (f_a(x)-1/2) + (f_a(-x)-1/2) = 0 なので,示せた。
証明終
シグモイド関数のグラフを見ればほぼ明らかな性質ですが,ちゃんと証明できました。
4. (f_a)’ = af_a(1-f_a) であること
4. \displaystyle f_a'(x) =a f_a(x)(1-f_a(x)).
証明
\begin{aligned} f'_a(x) &= \left(\frac{1}{1+e^{-ax}}\right)' \\ &= \frac{ae^{-ax}}{(1+e^{-ax})^2} \end{aligned}
である。一方,
なので,結論を得る。
証明終
元の関数から,直ちに微分が求まるのは,面白い性質ですね。ニューラルネットワークでシグモイド関数を使う際は,ネットワーク内部でこの性質をフルに活用し,計算を高速化しています。
なお,微分をグラフにすると以下のようになります。黒・緑はそれぞれ a=1,5 の場合を指します。
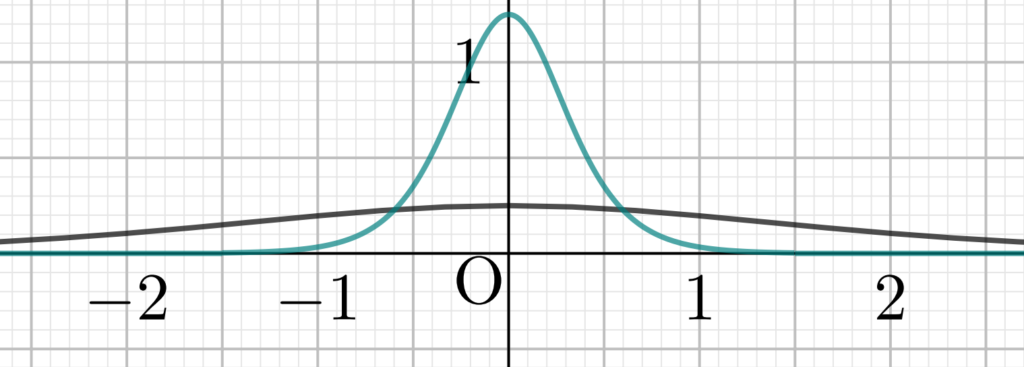
釣り鐘型の関数になっていますね。
6. シグモイド関数が双曲線関数でかけること
6. f_a は双曲線関数 \tanh を用いて, f_a(x) =\frac{1+\tanh(ax/2)}{2} とも表せる。
証明
\displaystyle \tanh x = \frac{e^x-e^{-x}}{e^x+e^{-x}} であるから,
\begin{aligned} f_a(x) &=\frac{1}{1+e^{-ax}}\\ &= \frac{1+\frac{e^{ax/2}-e^{-ax/2}}{e^{ax/2}+e^{-ax/2}}}{2}\\ &= \frac{1+\tanh(ax/2)}{2}\end{aligned}
となってわかる。
証明終
なお,双曲線関数 \tanh のグラフは以下のようになります。
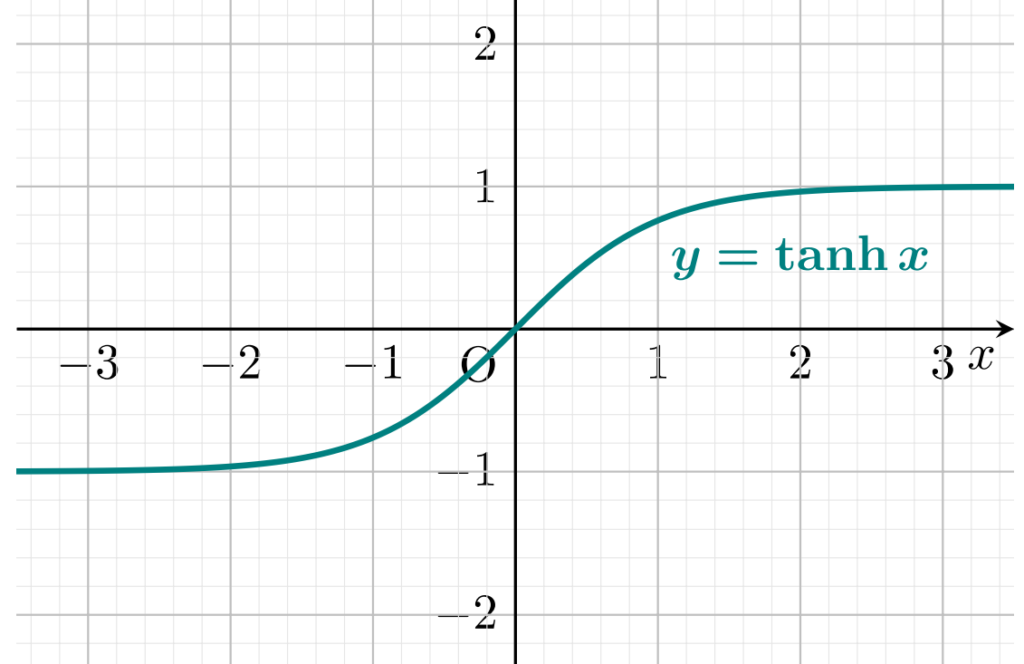
そもそもシグモイド関数のグラフと似ていることが分かりますね。
7. シグモイド関数の逆関数
7. \displaystyle f_a^{-1} (x) = \frac{1}{a}\log \frac{x}{1-x} \quad (0<x<1). (逆関数)
証明
f_a^{-1}\colon \mathbb{R}\to(-1,1) は全単射なので,逆関数が存在する。 y = f_a(x) = \frac{1}{1+e^{-ax}} とおくと,
\begin{aligned}&(1+e^{-ax})y = 1 \\ & \iff e^{-ax} = \frac{1-y}{y} \\ &\iff -ax = \log\frac{1-y}{y} \\ &\iff x = \frac{1}{a}\log\frac{y}{1-y} \end{aligned}
なので,\displaystyle f_a^{-1} (x) = \frac{1}{a}\log \frac{x}{1-x} \quad (0<x<1). である。
証明終
逆関数をグラフにすると,以下のようになります。 a=1 の場合です。
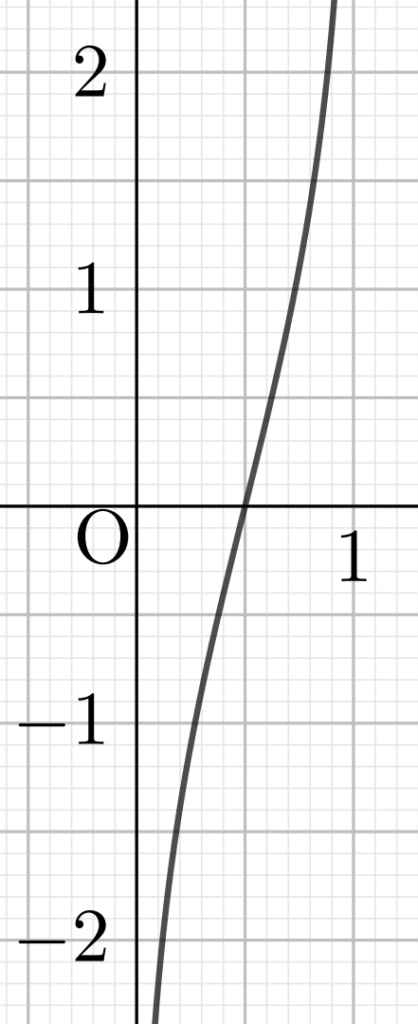
8. lim_{a→∞} f_a について
これは証明するまでもなく,
\lim_{a\to\infty} f_a(x) = \lim_{a\to\infty} \frac{1}{1+e^{-ax}} = \begin{cases} 1 & 0<x, \\ 1/2 & x=0,\\ 0 & x< 0 \end{cases}
となるのは明らかでしょう。ここで紹介したいのは,そのグラフです。以下の図を見てください。
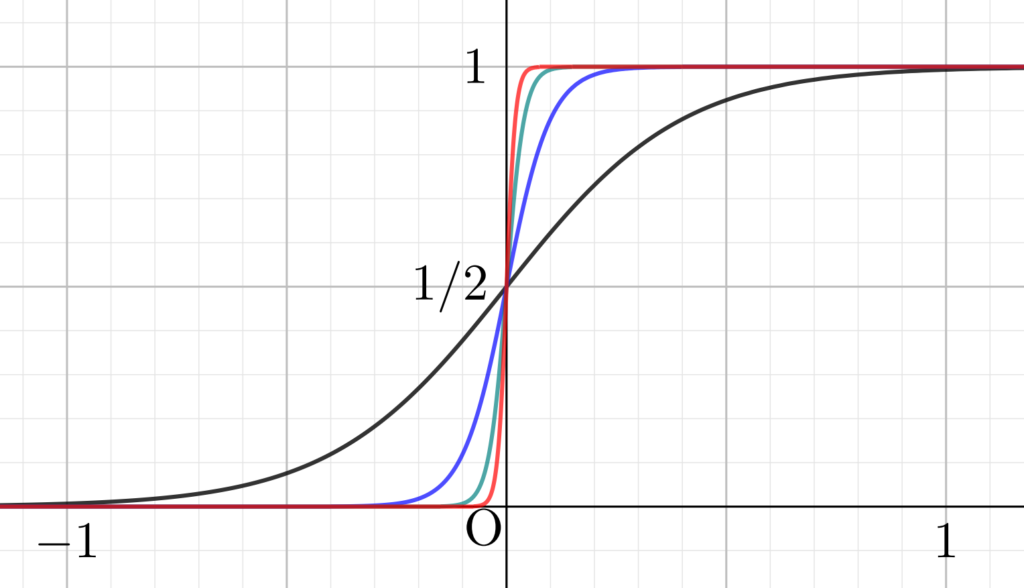
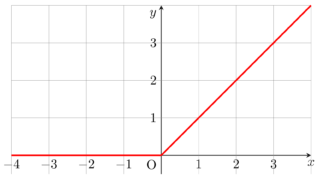
上の図は, a\to\infty とすると,グラフの傾きがどんどん急になっていくことを表しています。結局,極限は下のようなグラフにります。
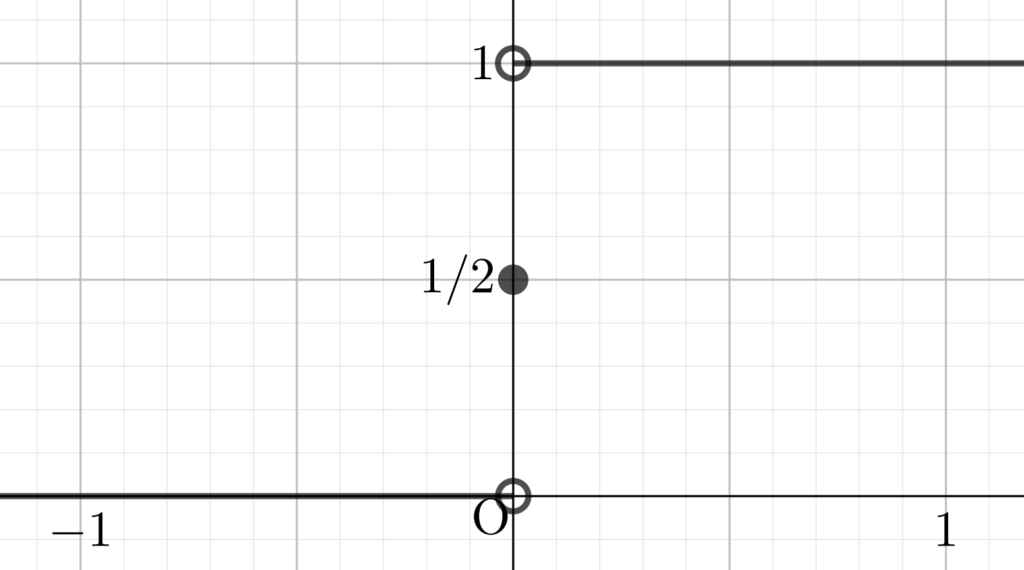
この極限関数は,ヘヴィサイドの階段関数 (Heaviside step function) と呼ばれることもあります。