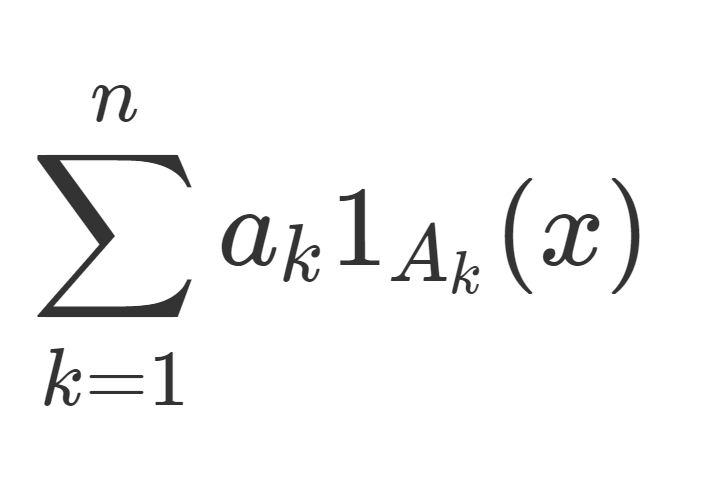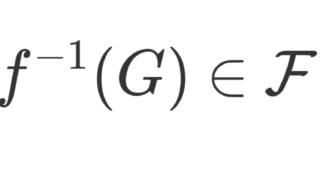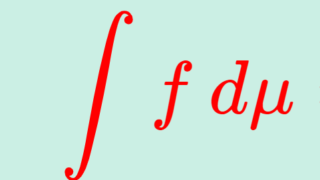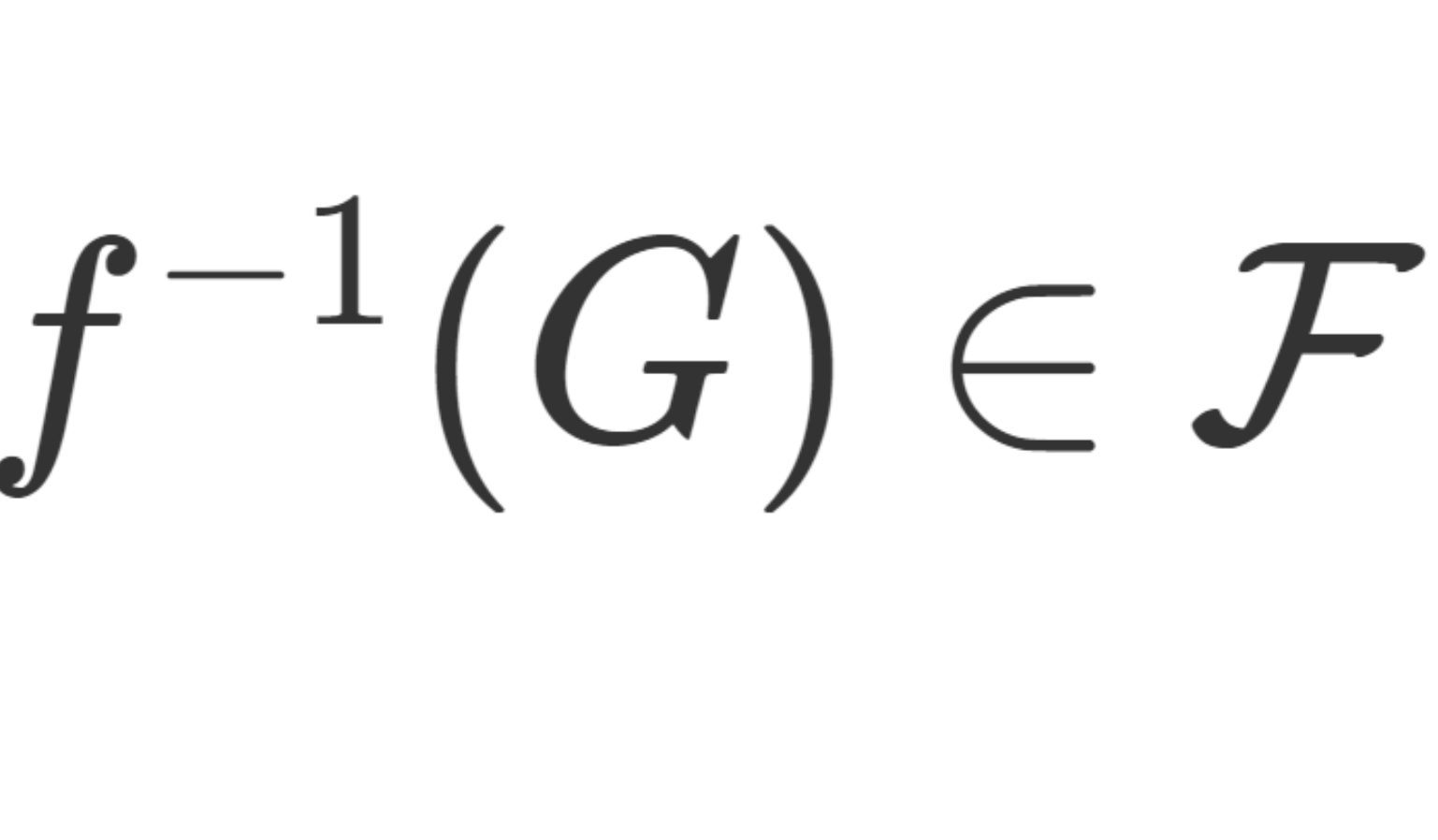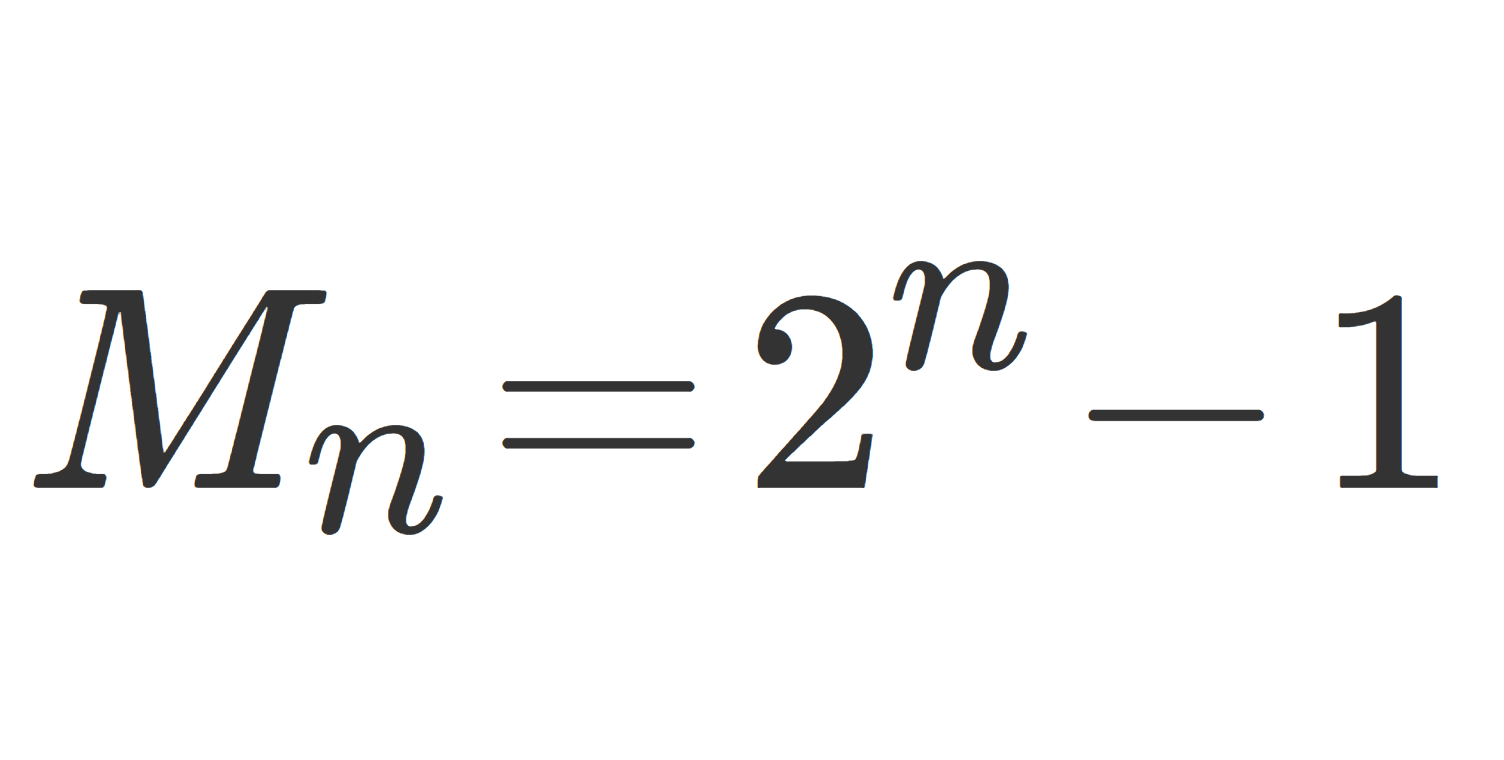(可測)単関数とは,実数 a_1, a_2,\dots, a_n と可測集合 A_1,A_2,\dots, A_n を用いて
f(x) = \sum_{k=1}^n a_k 1_{A_k} (x)
のようにかける可測関数のことを指します。
単関数の定義と「任意の可測関数は単関数で近似できること」の証明を解説しましょう。
単関数とは
定義(単関数)
(X,\mathcal{F}) を可測空間, f\colon X\to \mathbb{R} を可測関数とする。 f が有限個の値しか取らないとき,f を(可測)単関数 (simple function) という。
f が単関数のとき, a_1, a_2, \dots, a_n\in\mathbb{R} と,どの2つも互いに素な集合 A_1, A_2,\dots, A_n \in\mathcal{F} が存在して,
\large \color{red}f(x) = \sum_{k=1}^n a_k 1_{A_k} (x)
とかける。1_A(x)=\begin{cases} 1 & x\in A, \\ 0 & x\notin A \end{cases} は定義関数(指示関数)を指す。
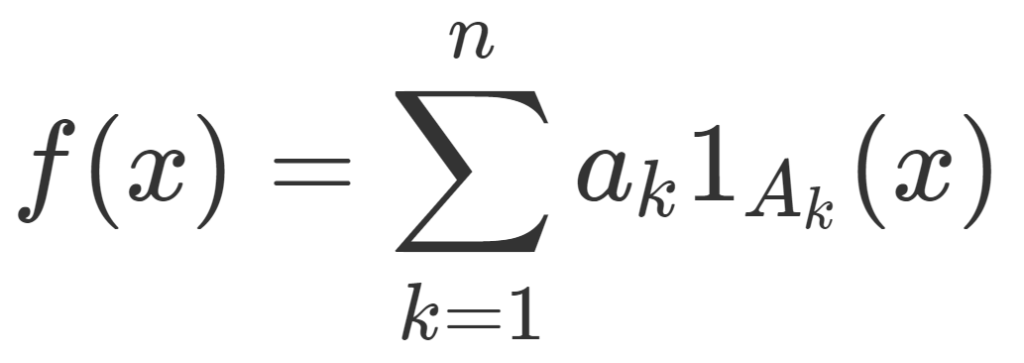
「 f が単関数のとき」以降の主張は簡単です。実際, f の値域を a_1, a_2, \dots, a_n\in\mathbb{R} とし, A_k = f^{-1} (a_k) \; (1\le k\le n) とすればよいです。1点集合は閉集合かつ f は可測より, A_k \in\mathcal{F} です。集合がどの2つも互いに素とは i\ne j \implies A_i\cap A_i =\emptyset を指します。
単関数の例を挙げましょう。定義域も \mathbb{R} とすることにします。
単関数の例
以下は単関数 f\colon \mathbb{R}\to \mathbb{R} の例である。
- 1_{[0, 1]} (x)
- 1_{(0, 1) } (x)
- 1_{[0, 1)}(x)
- 1_{\{a\} }(x) \quad (a\in\mathbb{R})
- \color{red} 1_{\mathbb{Q}}(x) (ディリクレ関数)
- \sum_{k=0}^{n-1} k^2 1_{[k, k+1)} (x)
- \color{red} 1_{\mathbb{Q}}(x)+ \sqrt{2}\cdot 1_{\mathbb{Q}+\sqrt{2}}(x)+\sqrt{3}\cdot 1_{\mathbb{Q}+\sqrt{3}}(x)
[0, 1], (0,1), [0,1), \{a\}, \mathbb{Q}\in\mathcal{B}(\mathbb{R}) (右辺は \mathbb{R} 上のボレル集合族のこと)。ですから,定義関数(指示関数)である1-5.は単関数ですね。特に, 1_\mathbb{Q}(x) のような複雑な関数も単関数になることに注意してください。
7.においては1点集合の可測性と \mathbb{Q} が可算集合であることから, \mathbb{Q}+\sqrt{2} = \{ q+\sqrt{2}\colon q\in\mathbb{Q}\} \in\mathcal{B}(\mathbb{R}) であり,同様に \mathbb{Q}+\sqrt{3}\in\mathcal{B}(\mathbb{R}) です。
可測関数は単関数で近似可能
非負の場合
任意の可測関数は単関数で近似可能です。まずは f\ge 0 としましょう。
定理1(非負可測関数は非負単関数で下から近似可能)
(X,\mathcal{F}) を可測空間, f\colon X\to \mathbb{R} を非負の可測関数とする。 このとき,非負可測単関数の増大列 \{f_n\} が存在して,各点で
\color{red} \large f_n(x) \uparrow f(x) \quad (n\uparrow \infty)
とできる。
f_n(x)\uparrow f(x) とは,各点 x\in\mathbb{R} において, f_1(x)\le f_{2} (x) \le f_{3}(x)\le \cdots (増大列) かつ f_n(x)\to f(x) を意味します。「増加して収束」って感じですね。収束は各点収束の意味です。
先ほどの例でも挙げましたが,単関数とは 1_\mathbb{Q} のようなものも該当することに注意してください。
証明
f_n(x) = \sum_{k=0}^{n2^n} \frac{k}{2^n} 1_{\{{k}/{2^n}\le f(x)<{(k+1)}/{2^n} \} }(x)
と定めると, \{f_n\} は可測単関数の増大列であり,任意の x\in X に対し, f(x)< n となるよう n を十分大きく取ると, 0\le f(x)-f_n(x) \le 1/2^n \xrightarrow{n\to\infty} 0 となるから,各点で f_n \uparrow f である。
証明終
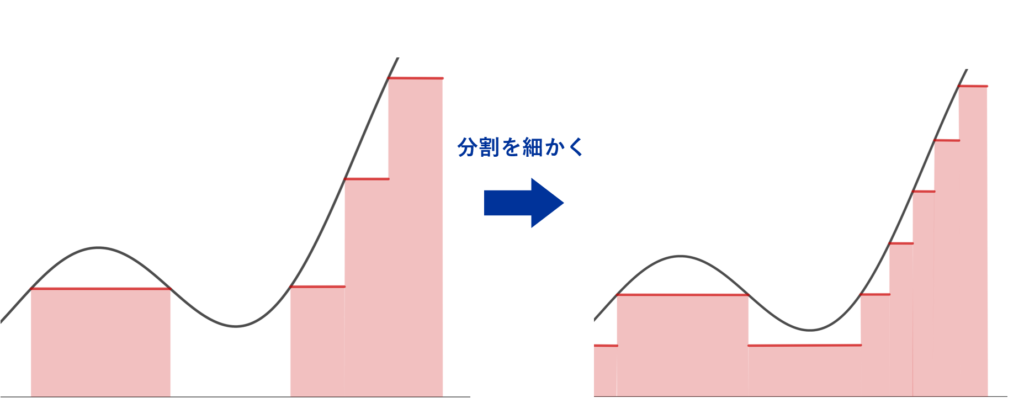
図解するとわかりやすいでしょう。以下のように,段々分割を細かくして下から近似します。
一般の場合
非負の条件を取ったのが以下の定理です。
定理2(可測関数は単関数で近似可能)
(X,\mathcal{F}) を可測空間, f\colon X\to \mathbb{R} を可測関数とする。 このとき,可測単関数の列 \{f_n\} が存在して,各点で
\color{red} \large f_n(x) \to f(x) \quad (n\uparrow \infty)
とできる。
証明は f を正の部分と負の部分に分けることで,定理1に帰着させればよいです。
証明
f^+ (x) = \max\{ f(x), 0\},\; f^- (x) = \max\{ -f(x), 0\} とすることで, f を正の部分と負の部分に分ける。これが可測関数であることはすぐわかる。 f=f^+ - f^- である。
定理1より,単関数列 \{f_n^+\}, \{f_n^-\} が存在して,各点で f_n^+\uparrow f^+,\, f_n^- \uparrow f^- \; (n\uparrow \infty) とできる。 f_n = f_n^+ - f_n^- とおくと, f_n \xrightarrow{n\uparrow\infty} f である。
証明終