双曲線関数 \sinh, \cosh, \tanh の定義とグラフについて解説し,さらにその性質を三角関数 \sin, \cos, \tan と比較しながらまとめます。
双曲線関数(sinh,cosh,tanh)の定義とグラフ
まずは sinh, cosh, tanh の定義を確認し,グラフを描きましょう。
双曲線関数の定義
定義(双曲線関数)
x\in \mathbb{R} に対し,
\color{red} \begin{aligned} \sinh x &= \frac{e^{x} - e^{-x} }{2}, \\ \cosh x &= \frac{e^{x} + e^{-x}}{2},\\ \tanh x &= \frac{\sinh x}{\cosh x} = \frac{ e^{x} - e^{-x}}{e^{x} + e^{-x}} \end{aligned}
を双曲線関数 (hyperbolic function) という。
\sinh, \cosh, \tanh はそれぞれハイパボリックサイン,ハイパボリックコサイン,ハイパボリックタンジェントと読みます。
双曲線関数のグラフ
それぞれのグラフを確認していきましょう。
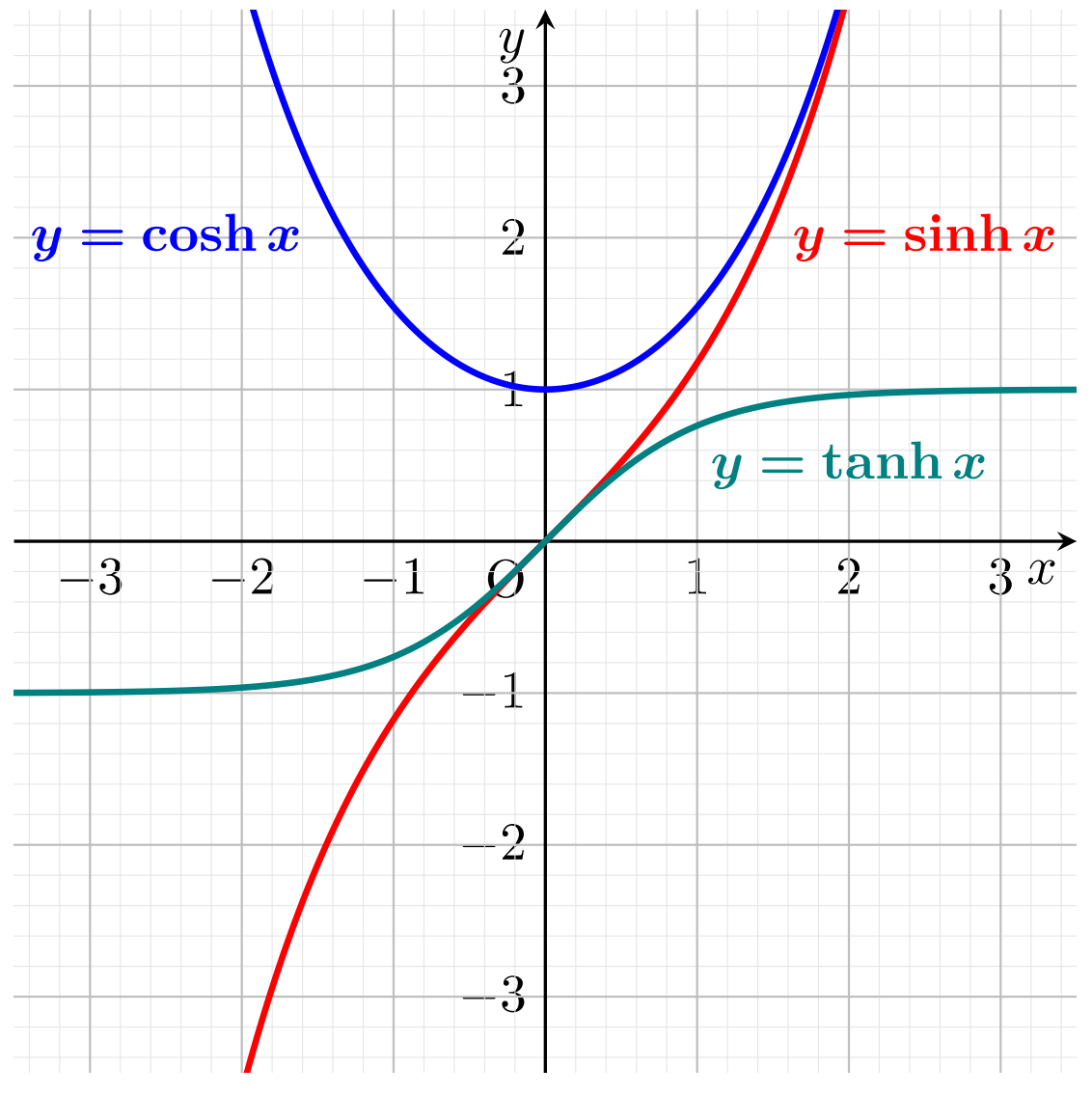
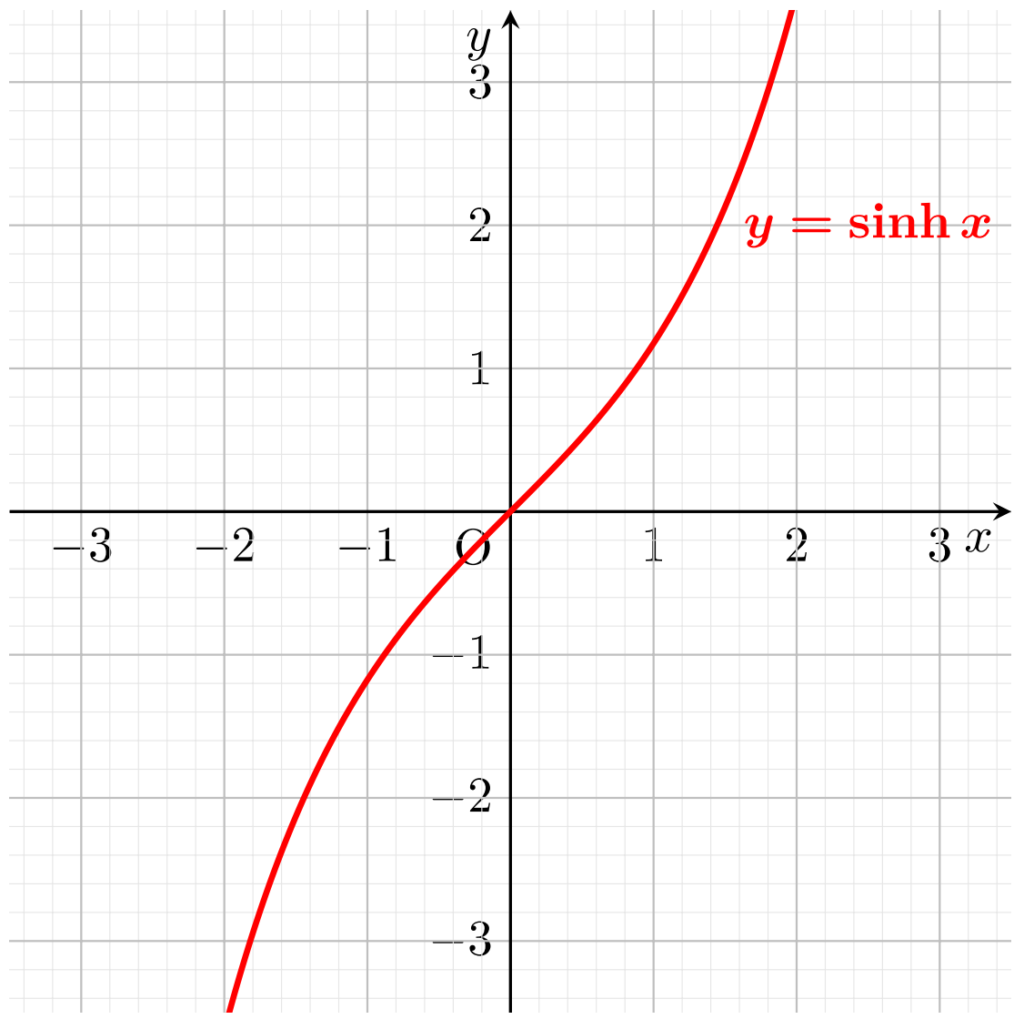
sinh のグラフ
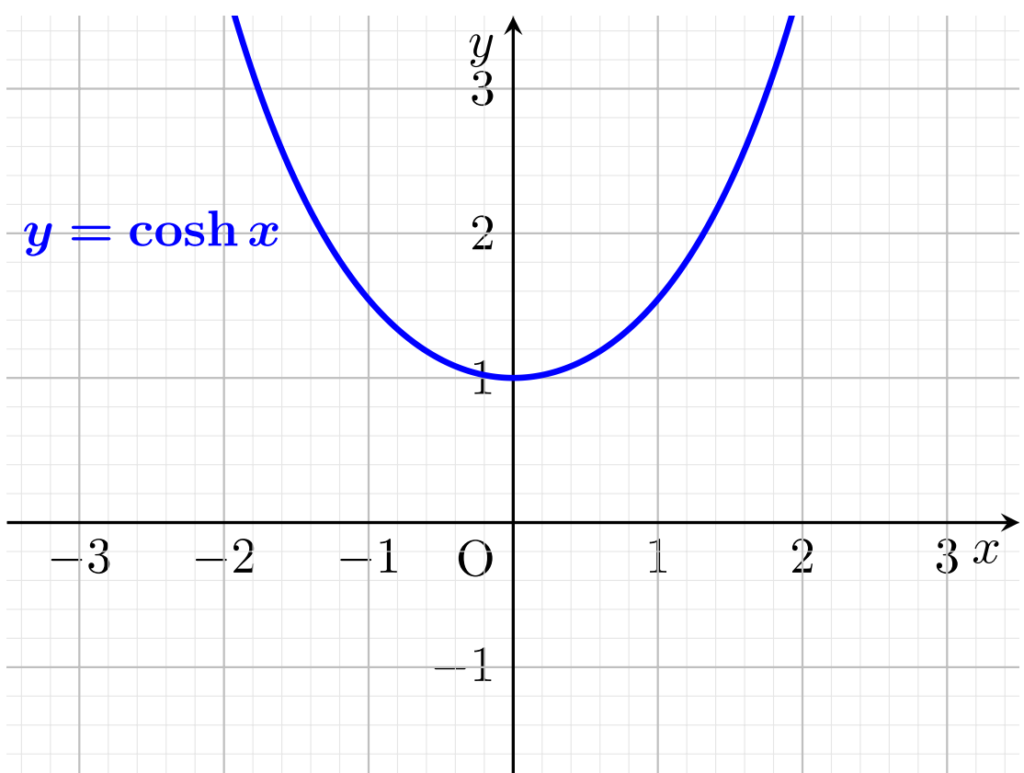
cosh のグラフ
tanh のグラフ
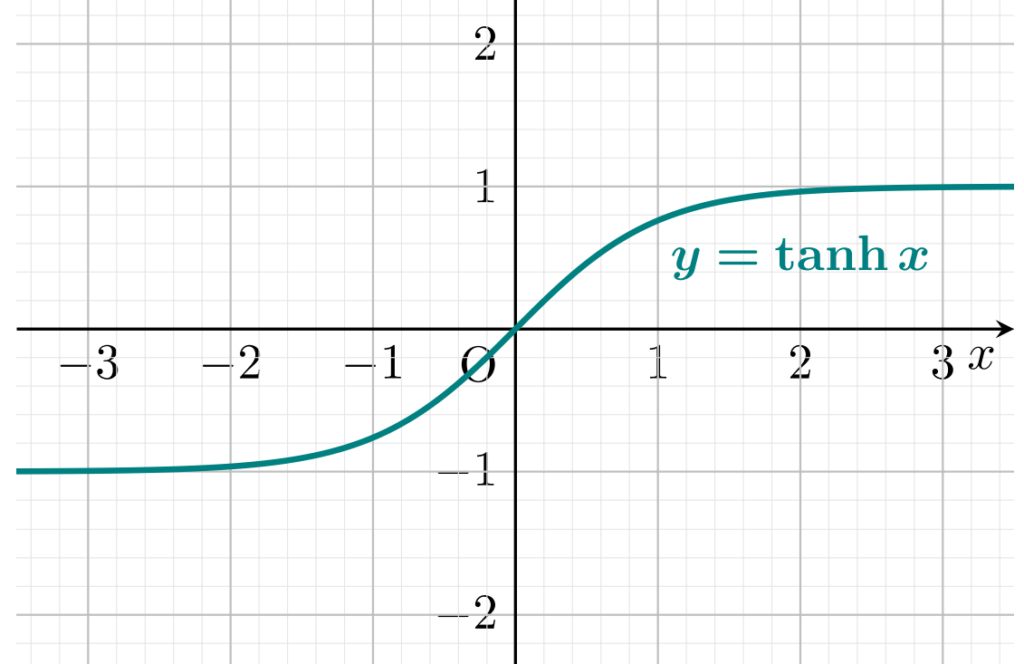
sinh, cosh, tanh のグラフをまとめて
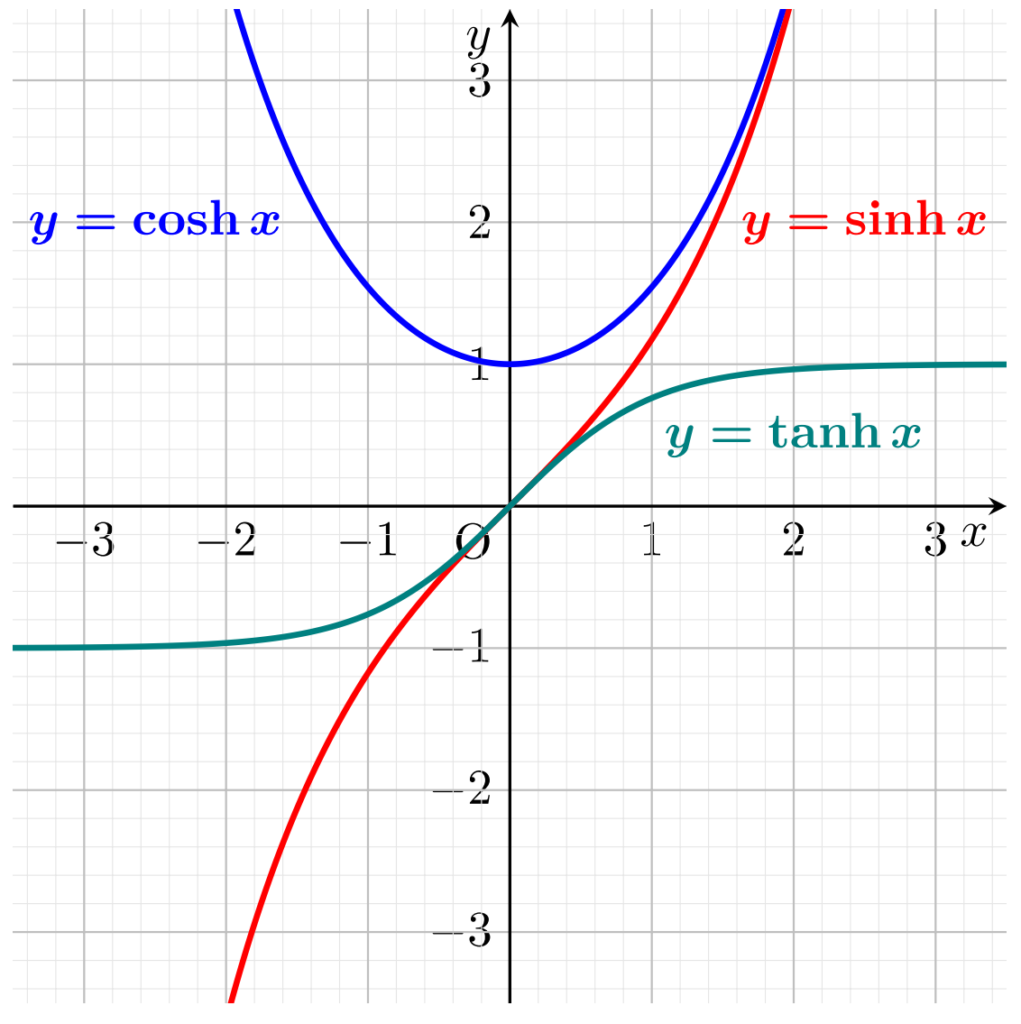
双曲線関数の性質
双曲線関数は三角関数と似たような性質がたくさんあります。これについて,「基本的な性質」「微分」「積分」「テイラー展開」にわけて確認していきましょう。
基本的な性質
まずは基本的な性質を確認しましょう。
定理(双曲線関数の基本的な性質)
- \sinh (-x) = - \sinh x. (奇関数)
- \cosh (-x) = \cosh x. (偶関数)
- \tanh (-x) = -\tanh x . (奇関数)
- \cosh^2 x - \sinh^2 x = 1.
- \displaystyle 1 - \tanh^2 x = \frac{1}{\cosh^2 x}.
- e^x = \cosh x + \sinh x.
- \sinh(\alpha \pm \beta) = \sinh \alpha \cosh \beta \pm \cosh\alpha \sinh \beta . ( \sinh の加法定理)
- \cosh(\alpha\pm \beta) = \cosh\alpha\cosh\beta \pm \sinh\alpha \sinh\beta. ( \cosh の加法定理)
- \displaystyle \tanh(\alpha\pm\beta) = \frac{\tanh\alpha \pm \tanh\beta}{1\pm \tanh \alpha \tanh \beta}. ( \tanh の加法定理)
- \displaystyle \lim_{x\to 0} \frac{\sinh x}{x} = 1. (極限)
4.の性質から,特に (\cosh x, \sinh x) の軌跡は双曲線の片側になります。これが,双曲線関数といわれる所以ですね。なお,三角関数は別名「円関数」と呼ばれます。
三角関数と比較してみましょう。
| 三角関数 | 双曲線関数 |
|---|---|
| \begin{aligned} \sin x = \frac{e^{ix} - e^{-ix} }{2i} \end{aligned} | \begin{aligned} \sinh x = \frac{e^x - e^{-x} }{2} \end{aligned} |
| \begin{aligned} \cos x = \frac{e^{ix} + e^{-ix}}{2} \end{aligned} | \begin{aligned} \cosh x = \frac{e^x + e^{-x}}{2} \end{aligned} |
| \begin{aligned} \tan x = \frac{\sin x}{\cos x} \end{aligned} | \begin{aligned} \tanh x = \frac{\sinh x }{\cosh x} \end{aligned} |
| \begin{aligned} \sin(-x) = -\sin x \end{aligned} | \begin{aligned} \sinh (-x) = - \sinh x \end{aligned} |
| \begin{aligned} \cos (-x) = \cos x \end{aligned} | \begin{aligned} \cosh (-x) = \cosh x \end{aligned} |
| \begin{aligned} \tan (-x) = -\tan x \end{aligned} | \begin{aligned} \tanh (-x) = -\tanh x \end{aligned} |
| \begin{aligned} \cos^2 x + \sin^2 x = 1 \end{aligned} | \begin{aligned} \cosh^2 x - \sinh^2 x = 1 \end{aligned} |
| \begin{aligned} 1 + \tan^2 x = \frac{1}{\cos^2 x} \end{aligned} | \begin{aligned} 1 - \tanh^2 x = \frac{1}{\cosh^2 x} \end{aligned} |
| \begin{aligned} e^{ix} = \cos x + i \sin x \end{aligned} | \begin{aligned} e^x = \cosh x + \sinh x \end{aligned} |
| \begin{aligned} \sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos\alpha \sin \beta \end{aligned} | \begin{aligned} \sinh(\alpha \pm \beta) = \sinh \alpha \cosh \beta \pm \cosh\alpha \sinh \beta \end{aligned} |
| \begin{aligned} \cos(\alpha\pm \beta) = \cos\alpha\cos\beta \mp \sin\alpha\sin\beta \end{aligned} | \begin{aligned} \cosh(\alpha\pm \beta) = \cosh\alpha\cosh\beta \pm \sinh\alpha\sinh\beta \end{aligned} |
| \begin{aligned} \tan(\alpha\pm\beta) = \frac{\tan\alpha \pm \tan\beta}{1\mp \tan \alpha \tan \beta} \end{aligned} | \begin{aligned} \tanh(\alpha\pm\beta) = \frac{\tanh\alpha \pm \tanh\beta}{1\pm \tanh \alpha \tanh \beta} \end{aligned} |
| \begin{aligned} \lim_{x\to 0} \frac{\sin x}{x} = 1 \end{aligned} | \begin{aligned} \lim_{x\to 0} \frac{\sinh x}{x} = 1 \end{aligned} |
符号の違いはあれど,かなり性質は似ていますね。
双曲線関数の微分
双曲線関数の微分の性質も,かなり三角関数と似ています。
定理(双曲線関数の微分)
- \displaystyle (\sinh x)' = \cosh x.
- \displaystyle (\cosh x)' = \sinh x.
- \displaystyle (\tanh x)' = \frac{1}{\cosh^2 x} = 1 - \tanh^2 x .
再び三角関数と比較してみましょう。
| 三角関数 | 双曲線関数 |
|---|---|
| \displaystyle (\sin x)' = \cos x | \displaystyle (\sinh x)' = \cosh x |
| \displaystyle (\cos x)' = -\sin x | \displaystyle (\cosh x)' = \sinh x |
| \displaystyle (\tan x)' = \frac{1}{\cos^2 x} = 1 + \tan^2 x | \displaystyle (\tanh x)' = \frac{1}{\cosh^2 x} = 1 - \tanh^2 x |
これも符号は違えど,性質は似ていますね。
双曲線関数の積分
微分の公式を逆に用いると,積分の公式が作れます。
定理(双曲線関数の積分)
- \int \sinh x \, dx = \cosh x + C.
- \int \cosh x \, dx = \sinh x + C.
- \int \tanh x \, dx = \log( \cosh x) + C = \log(e^x + e^{-x} ) + C'.
- \displaystyle \int \frac{1}{\cosh^2 x} \, dx = \tanh x + C.
ただし, C, C' は積分定数。
3.のみは微分の逆とは言えませんね。これは \displaystyle \int \frac{f'(x)}{f(x)} \, dx = \log |f(x)| + C を使えば導出できます。
これも三角関数と比較しましょう。
| 三角関数 | 双曲線関数 |
|---|---|
| \int \sin x \, dx = - \cos x + C | \int \sinh x \, dx = \cosh x + C |
| \int \cos x \, dx = \sin x + C | \int \cosh x \, dx = \sinh x + C |
| \int \tan x\, dx = \log |\cos x| + C | \int \tanh x \, dx = \log (\cosh x) + C |
| \displaystyle \int \frac{1}{\cos^2 x} \, dx = \tan x + C | \displaystyle \int \frac{1}{\cosh^2 x} \, dx = \tanh x + C |
sinh, cosh のテイラー展開(マクローリン展開)
双曲線関数,特に \sinh, \cosh の0でのテイラー展開(マクローリン展開)を述べておきましょう。すべて x \in \mathbb{R} で成立します。
定理(sinh, cosh のテイラー展開)
- \displaystyle \sinh x = \sum_{n=0}^\infty \frac{x^{2n+1}}{(2n+1)!} = x + \frac{x^3}{3!} + \frac{x^5}{5!} +\frac{x^7}{7!}+ \cdots
- \displaystyle \cosh x = \sum_{n=0}^\infty \frac{x^{2n}}{(2n)!} = 1+ \frac{x^2}{2!} + \frac{x^4}{4!} + \frac{x^6}{6!} + \cdots
| 三角関数 | 双曲線関数 |
|---|---|
| \displaystyle \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots | \displaystyle \sinh x = x + \frac{x^3}{3!} + \frac{x^5}{5!} + \frac{x^7}{7!}+ \cdots |
| \displaystyle \cos x = 1- \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots | \displaystyle \cosh x = 1+ \frac{x^2}{2!} + \frac{x^4}{4!} + \frac{x^6}{6!} +\cdots |
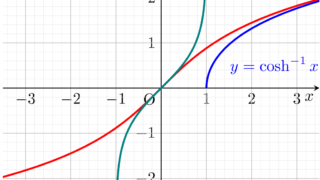
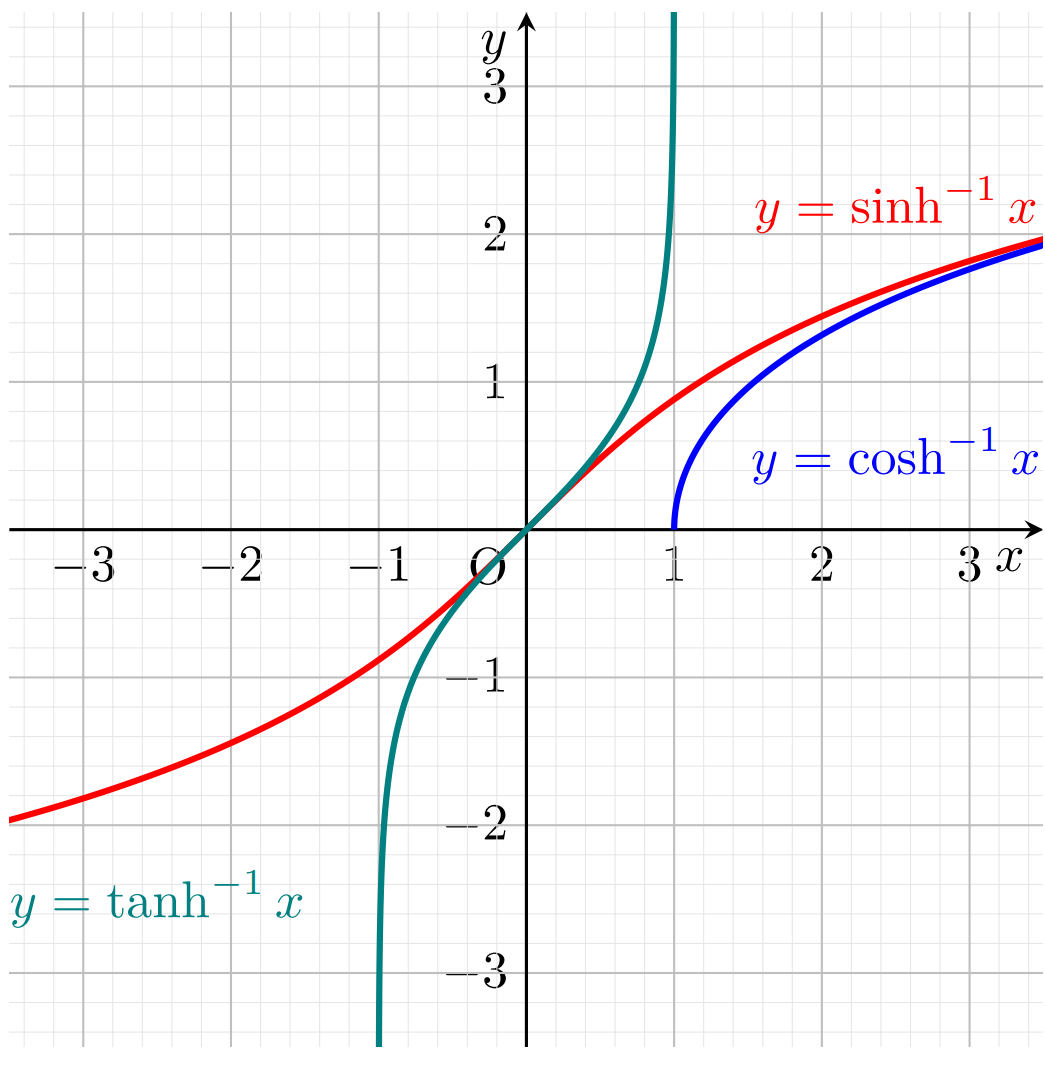
双曲線関数の逆関数
グラフを見るとわかるように, \sinh, \tanh はそれぞれ終域を \mathbb{R}, (-1,1) とすることで全単射になります。また \cosh は定義域を x \ge 0 に制限し,終域を y\ge 1 とすることで,全単射になります。これにより,逆関数を考えることができます。
双曲線関数の逆関数は,既存の関数を用いて表すことができます。
定理(双曲線関数の逆関数;逆双曲線関数)
- \sinh^{-1} x = \log(x+\sqrt{x^2+1}), \quad x \in \mathbb{R}.
- \cosh^{-1} x = \log(x+\sqrt{x^2-1}), \quad x\ge 1 .
- \displaystyle \tanh^{-1} x = \frac{1}{2} \log \frac{1+x}{1-x}, \quad -1<x<1.
逆双曲線関数を用いると,有名な積分の公式を得ることができます。
a> 0 とする。
- \color{red} \displaystyle \int \frac{dx}{\sqrt{x^2 + a^2} } = \sinh^{-1} \frac{x}{a} + C= \log(x+\sqrt{x^2+a^2}) + C'.
- \color{red} \displaystyle \int \frac{dx}{\sqrt{x^2-a^2}} = \cosh^{-1} \frac{x}{a} + C = \log(x+\sqrt{x^2-a^2}) + C', \,\, x \ge a.
ただし, C, C' は積分定数。
詳しくは以下の記事で解説しています。