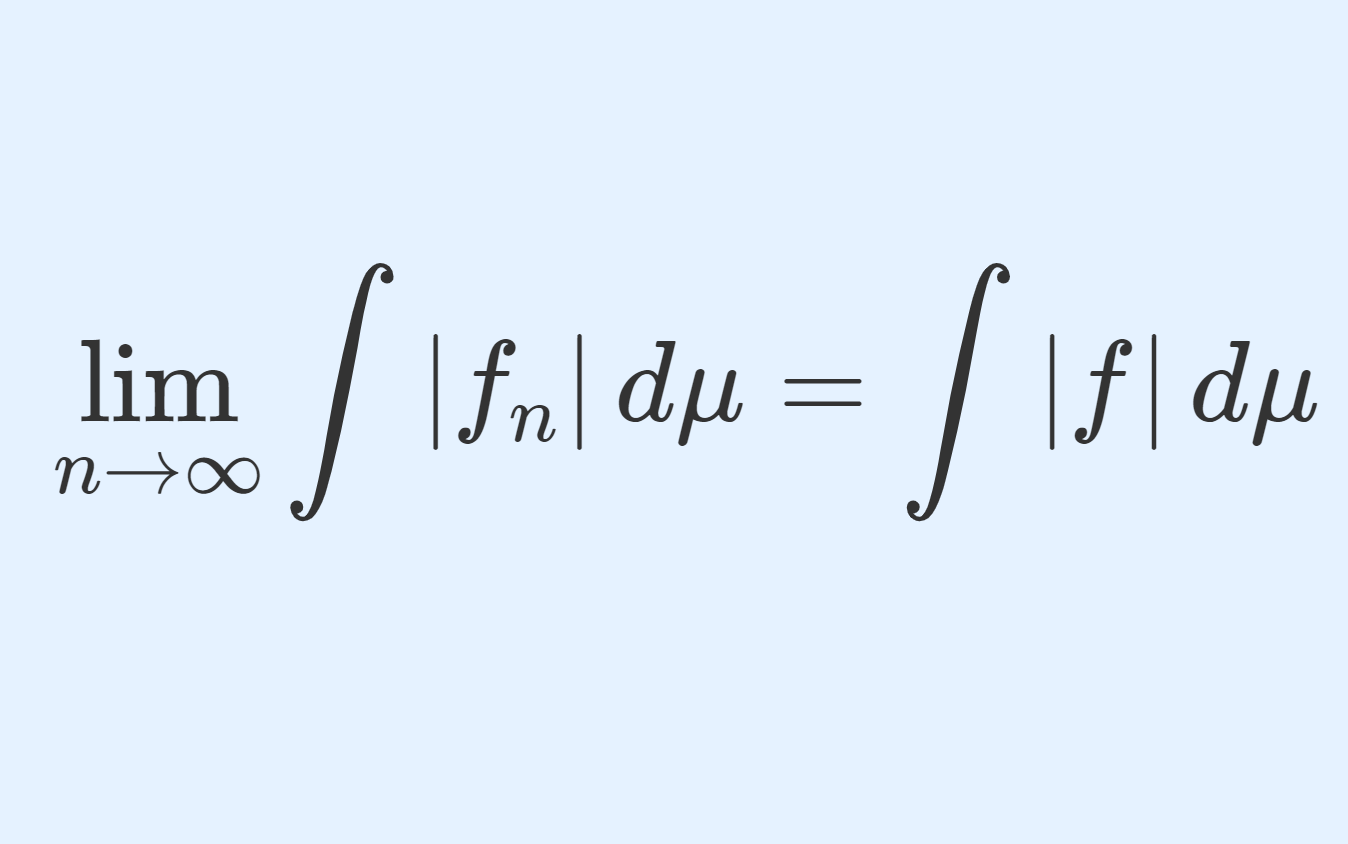関数の台 (support) とは定義域の,値が消滅しない部分集合 \{ x\in X\mid f(x)\ne 0\} やその閉包 \overline{\{ x\in X\mid f(x)\ne 0\}} を指します。これについて,もう少し掘り下げて解説しましょう。
関数の台(supp)とは
定義(関数の台(supp))
関数 f\colon X\to \mathbb{R} (または \mathbb{C}) の定義域 X における,値が消滅しない部分集合
\operatorname{Supp} f = \{ x\in X\mid f(x)\ne 0\}
を関数の台 (support) という。 X が位相空間のときは普通
と定義する(ただし上付きバーは閉包 (closure) を表す)。
大学数学で \operatorname{Supp} f を使うときは後者の意味(閉包を取る方)が多いですね(それ以上の数学になると分野によると思います)。 \mathbb{R} は位相空間ですから, f\colon \mathbb{R}\to\mathbb{R} を考えるときの \operatorname{Supp} f も普通後者の意味です。
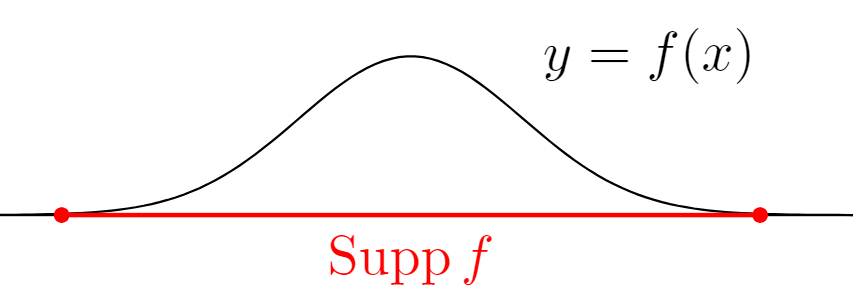
X を位相空間とし, f\colon X\to \mathbb{R} を連続関数としましょう。このとき,
\{x\in X\mid f(x)\ne 0\} = X\setminus f^{-1}(0)
で,逆像 f^{-1}(0)(=f^{-1}(\{0\})) は閉集合ですから, \{x\in X\mid f(x)\ne 0\} は開集合になります。これの閉包を取ることで, \operatorname{Supp} f を閉集合にしています。
なお, \operatorname{Supp} を間違えて \sup と書いてしまうと上限 (supremum) の意味になってしまうので注意しましょう。
コンパクト台を持つ関数
大学の数学では compact support な関数をよく扱います。これは,台(support) がコンパクト集合である関数を指します。
定義(コンパクト台を持つ関数)
コンパクトな台を持つ関数全体の集合を
\color{red} C_c(\mathbb{R})=\{ f\colon\mathbb{R}\to\mathbb{C}\mid \operatorname{Supp} f \text{ is compact}\}
とかく。ただし,\operatorname{Supp} f =\overline{ \{ x\in \mathbb{R}\mid f(x)\ne 0\} } である。
関数の終域は \mathbb{R} にすることもあります。
\mathbb{R} 上では,「コンパクト\iff 有界閉集合」であり,台(supp)は定義で閉集合にしていますから,上の定義は単に \{x\in\mathbb{R}\mid f(x)\ne 0\} が有界な関数の集合といっているだけですね。
コンパクトな台を持つ関数は,任意の連続関数を近似できることが知られています。この辺の話は関数解析学の話ですから,別の機会に解説しましょう。