 記号・記法
記号・記法 二項演算・単項演算とは
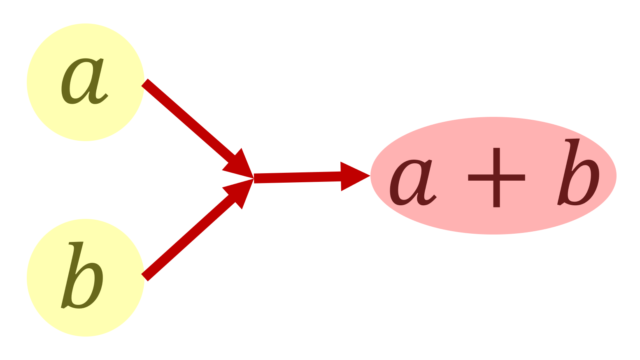
二項演算 (binary operation)・単項演算 (unary operation) は,厳密には集合上の写像として定義されます。これについて,その定義と例を紹介しましょう。
 記号・記法
記号・記法  解析学(大学)その他
解析学(大学)その他 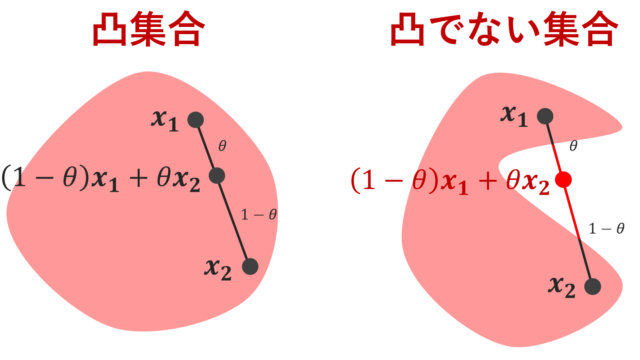 解析学(大学)その他
解析学(大学)その他  群・環・体
群・環・体 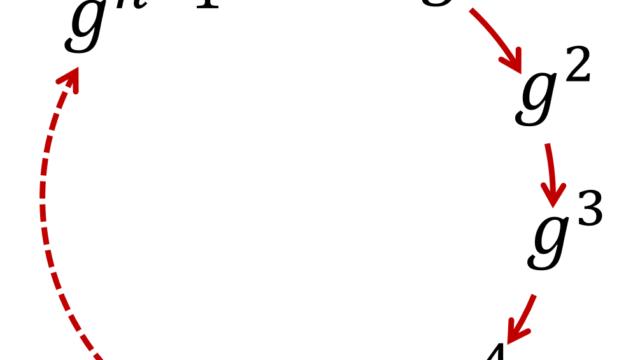 群・環・体
群・環・体  群・環・体
群・環・体 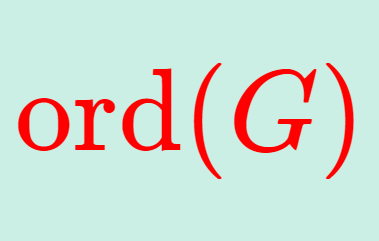 群・環・体
群・環・体 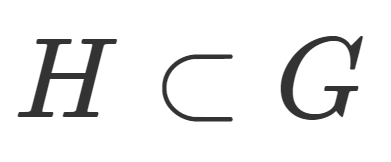 群・環・体
群・環・体  統計学
統計学 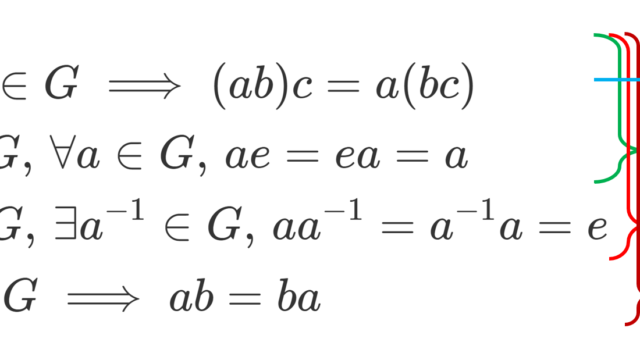 群・環・体
群・環・体