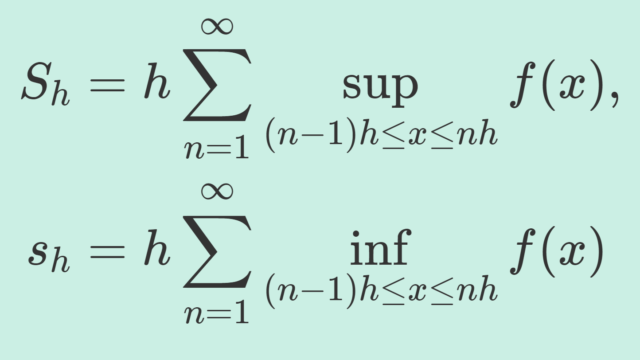 解析学(大学)その他
解析学(大学)その他 Directly Riemann Integrableの定義と例
無限区間でリーマン和(区分求積)を考えることが可能である Directly Riemann Integrable (dRi) な関数について,その定義と例を紹介します。
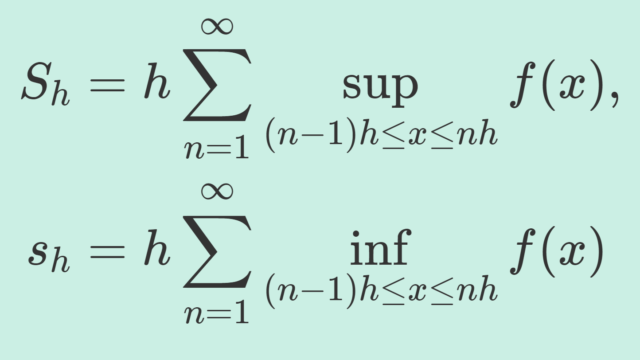 解析学(大学)その他
解析学(大学)その他  微分積分学(大学)
微分積分学(大学)  線形代数学
線形代数学  集合と位相
集合と位相  集合と位相
集合と位相  解析学(大学)その他
解析学(大学)その他  集合と位相
集合と位相 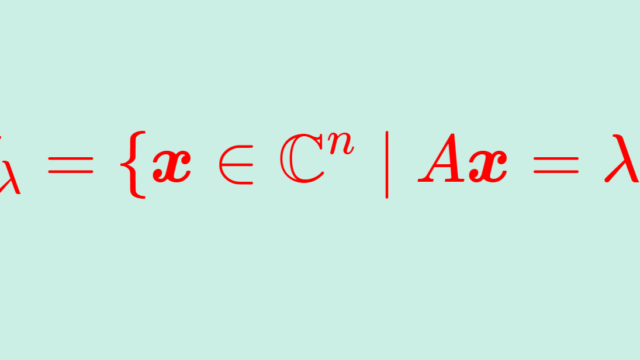 線形代数学
線形代数学 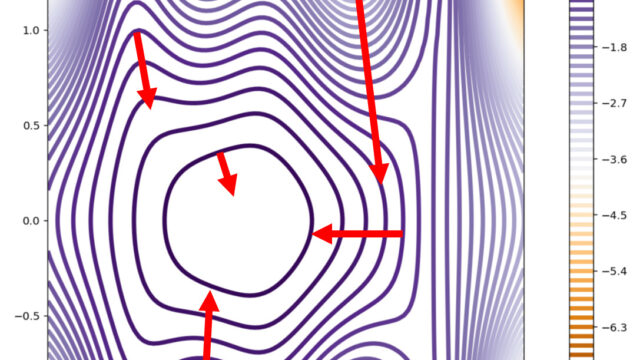 微分積分学(大学)
微分積分学(大学) 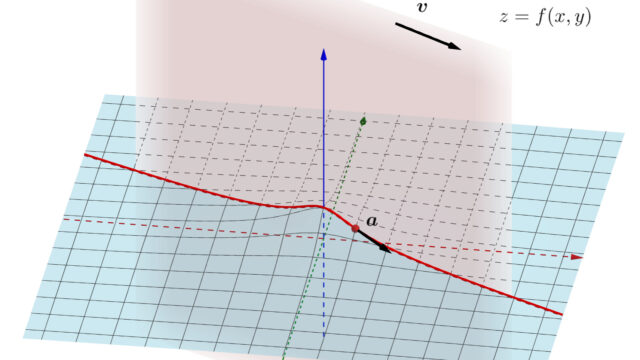 微分積分学(大学)
微分積分学(大学)