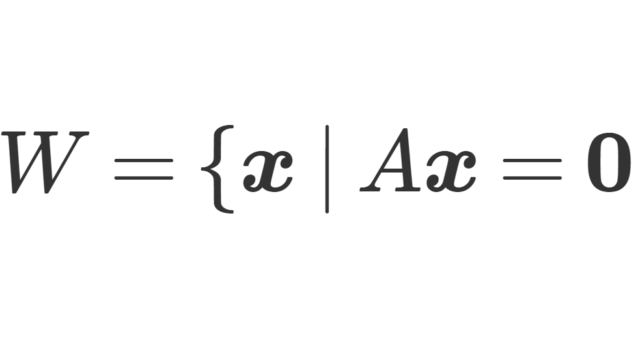 線形代数学
線形代数学 連立一次方程式の基本解・特殊解と解空間の性質
連立一次方程式における,基本解 (fundamental solution)・特殊解 (particular solution) と解空間 (solution space) の定義とその性質について,理解しておくべき重要な事項を紹介し,証明しましょう。
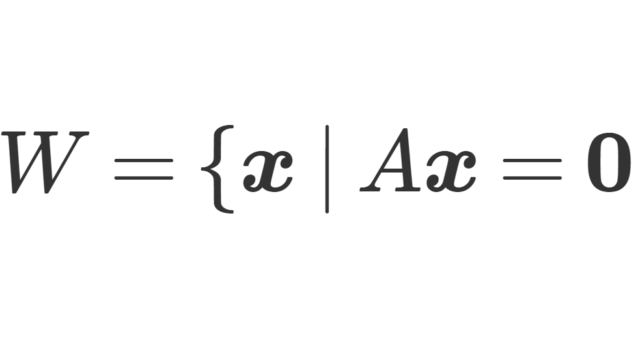 線形代数学
線形代数学  線形代数学
線形代数学  微分積分学(大学)
微分積分学(大学) 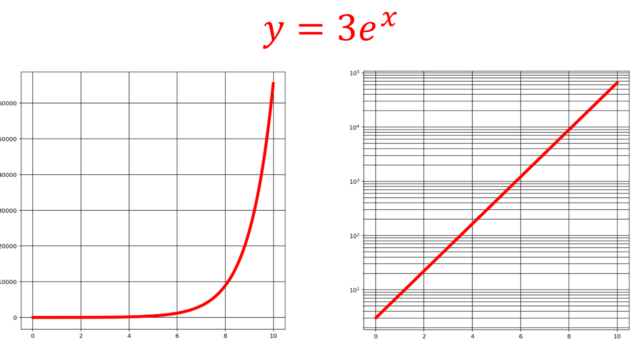 統計学
統計学 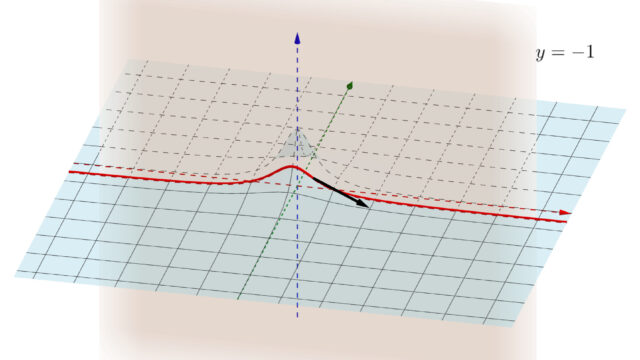 微分積分学(大学)
微分積分学(大学) 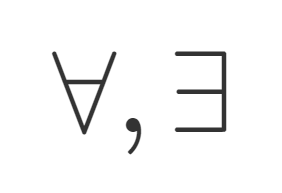 記号・記法
記号・記法 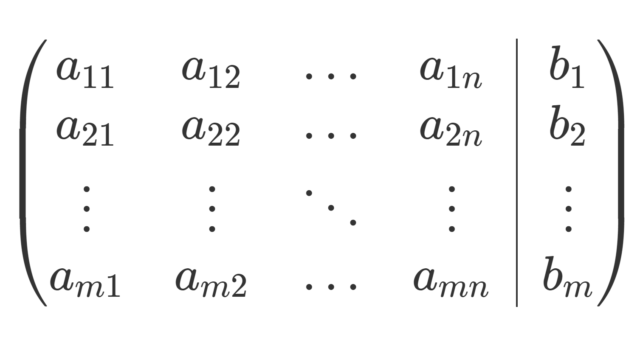 線形代数学
線形代数学 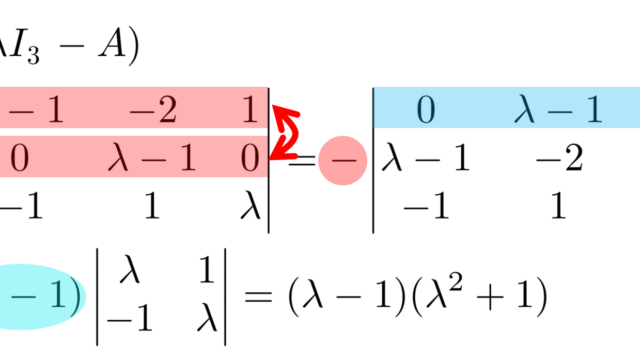 線形代数学
線形代数学 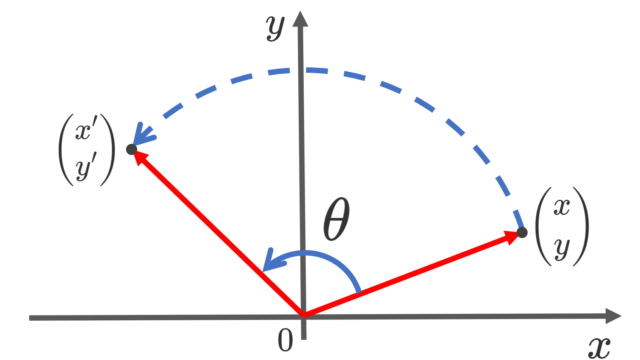 線形代数学
線形代数学 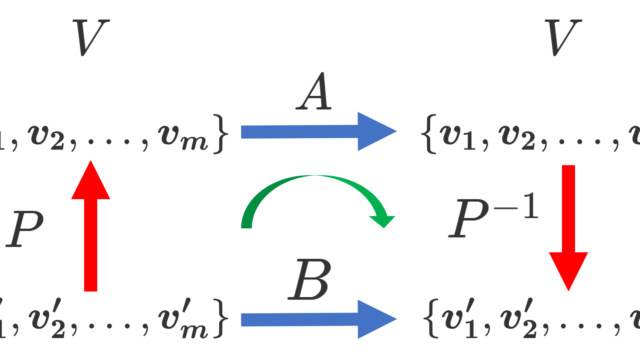 線形代数学
線形代数学