 線形代数学
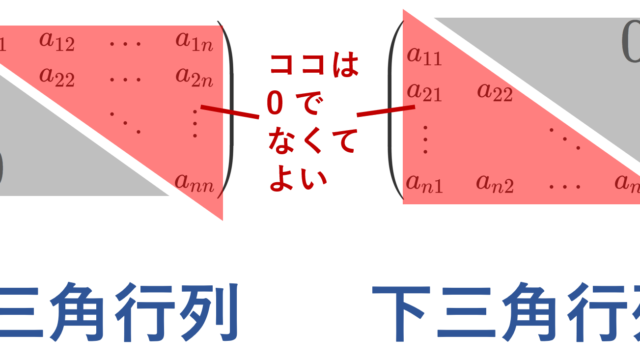
線形代数学 上三角行列・下三角行列の定義と性質6つ
正方行列における,上三角行列 (あるいは右三角行列)・下三角行列 (あるいは左三角行列)・三角行列 (triangular matrix) の定義と,その性質6つを紹介します。
 線形代数学
線形代数学 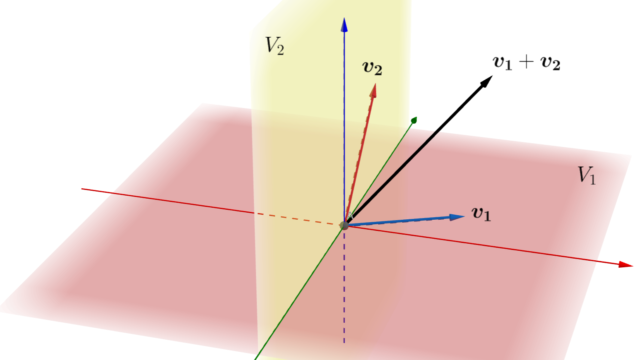 線形代数学
線形代数学 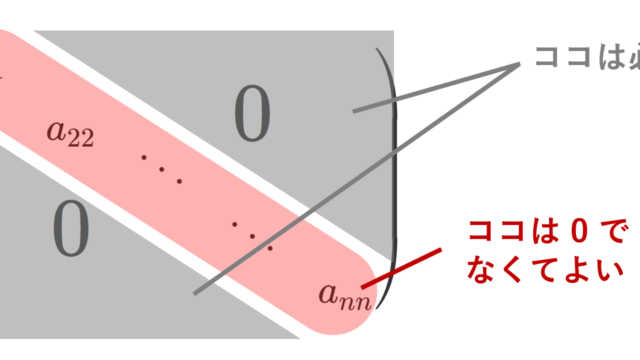 線形代数学
線形代数学 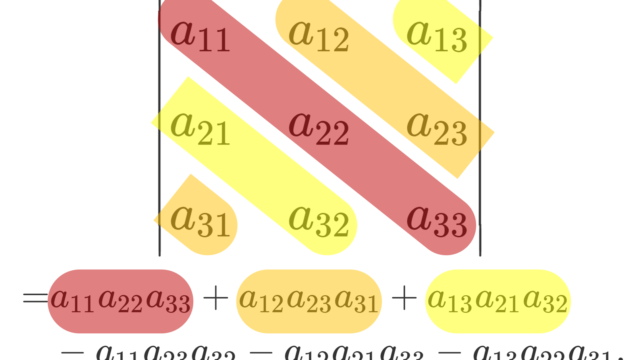 線形代数学
線形代数学 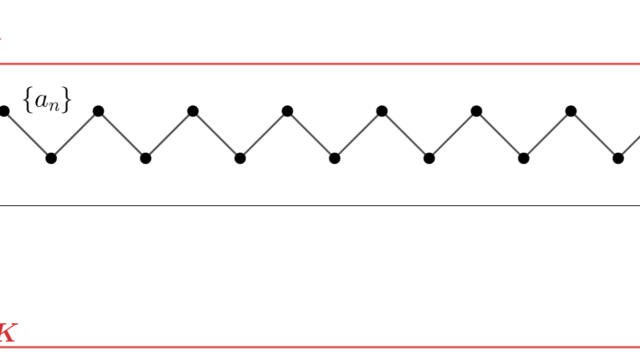 微分積分学(大学)
微分積分学(大学) 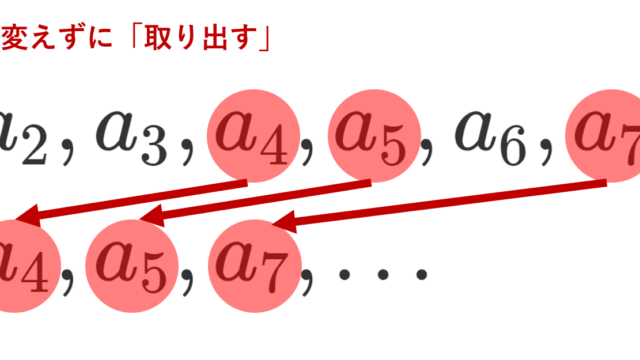 微分積分学(大学)
微分積分学(大学) 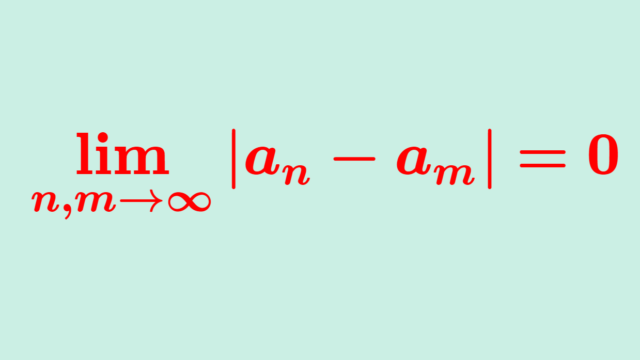 微分積分学(大学)
微分積分学(大学) 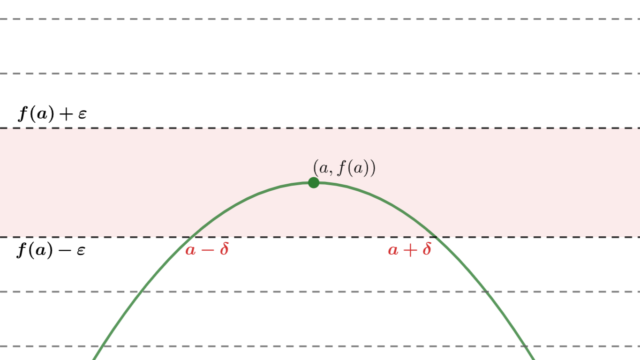 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  線形代数学
線形代数学