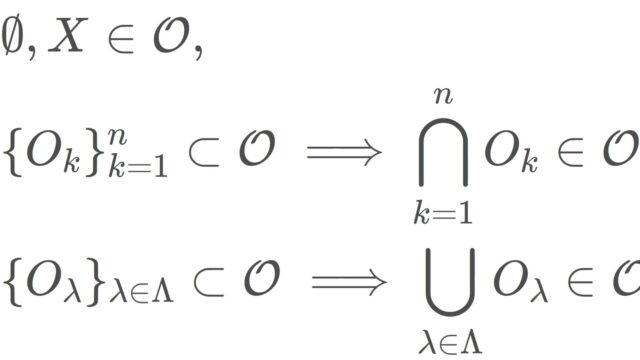 集合と位相
集合と位相 位相空間の定義と開集合・閉集合について
位相空間とは,点の近さを土台とする「収束性・写像の連続性」が議論できる抽象的な空間といえます。その定義はかなり抽象的なものですが,ユークリッド空間や距離空間でなくても,さらに一般的に広く収束・連続の概念を取り扱うことができ,大学以上の数学を深めるうえで欠かすことのできない概念です。
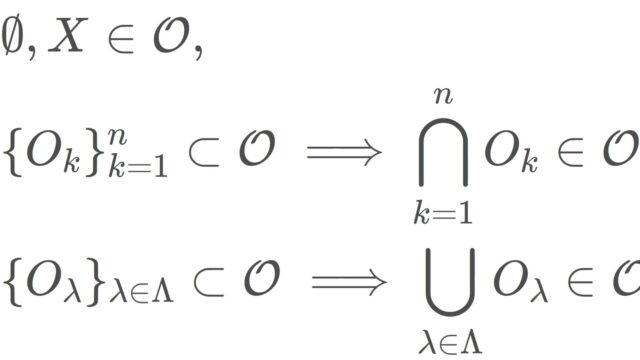 集合と位相
集合と位相  記号・記法
記号・記法 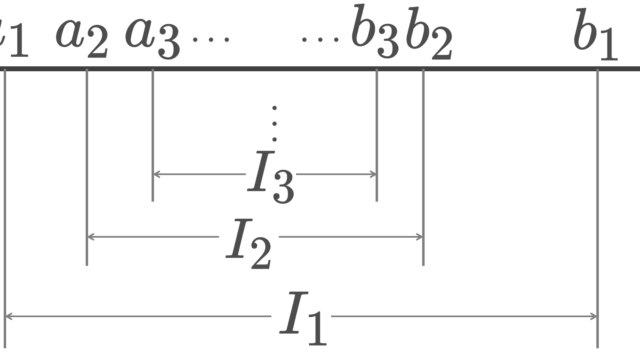 解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他 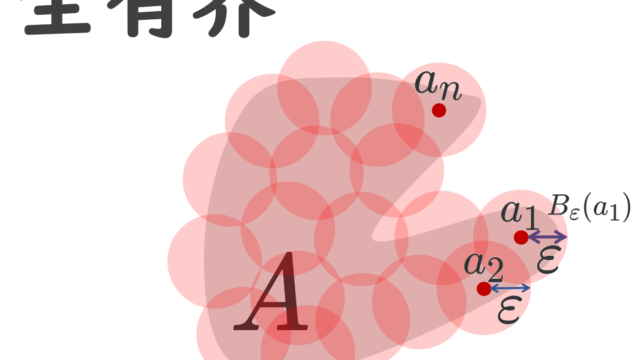 集合と位相
集合と位相 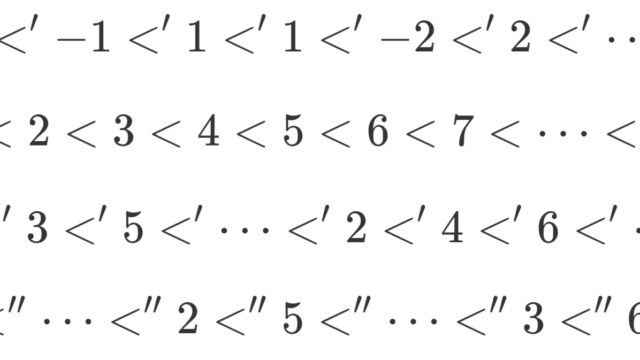 集合と位相
集合と位相 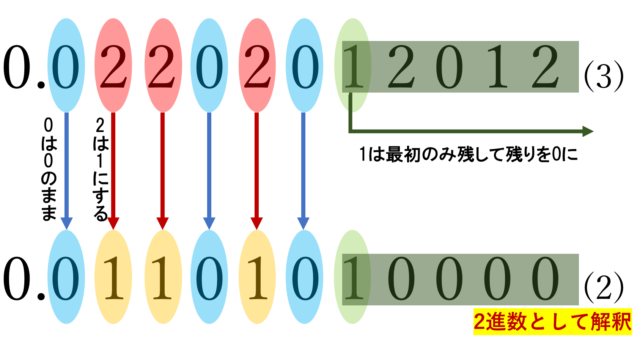 解析学(大学)その他
解析学(大学)その他 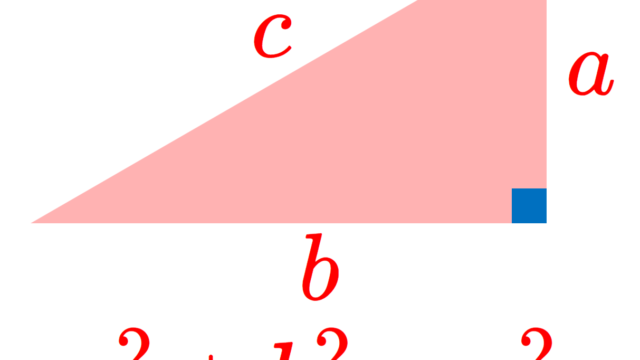 数論
数論 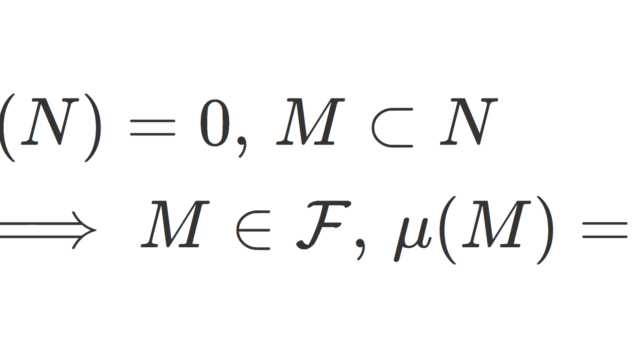 測度論
測度論  解析学(大学)その他
解析学(大学)その他