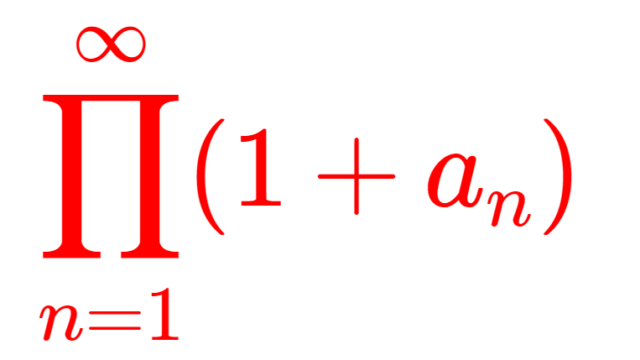 解析学(大学)その他
解析学(大学)その他 無限積の定義と性質・無限和の収束との関係
無限積あるいは無限乗積 (infinite product) とは,無限個の積のことをいいます。無限積の定義と,その収束性について,無限和との関連性や絶対収束を含めて述べましょう。
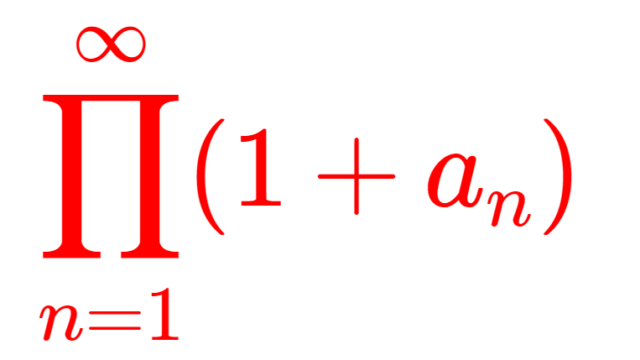 解析学(大学)その他
解析学(大学)その他 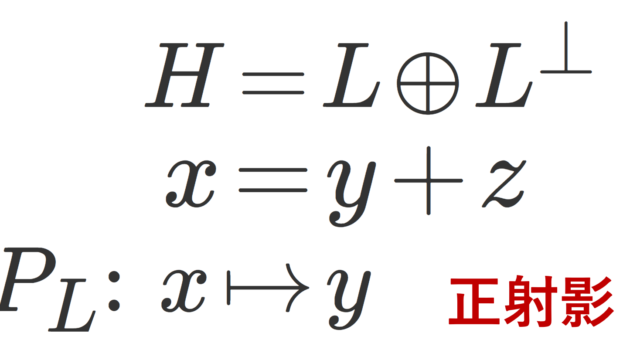 関数解析学
関数解析学 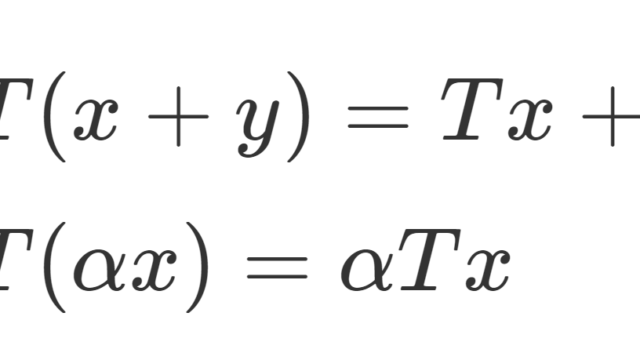 関数解析学
関数解析学 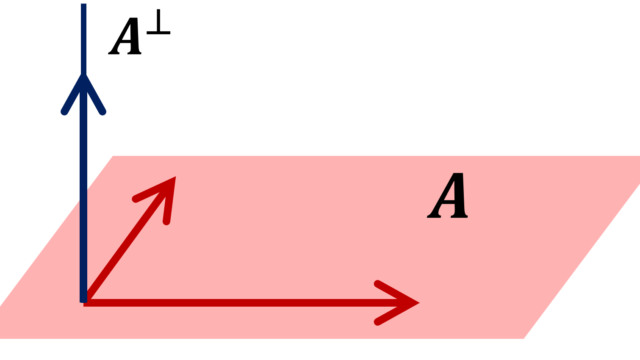 関数解析学
関数解析学 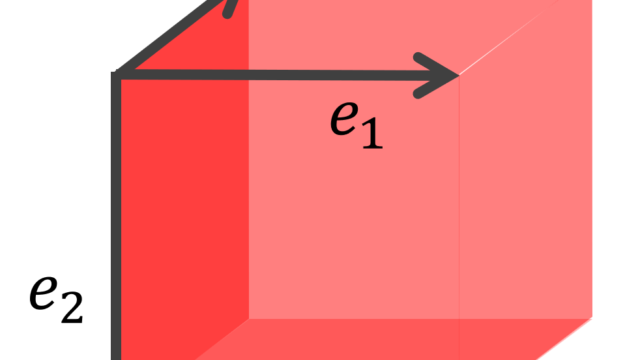 関数解析学
関数解析学  関数解析学
関数解析学 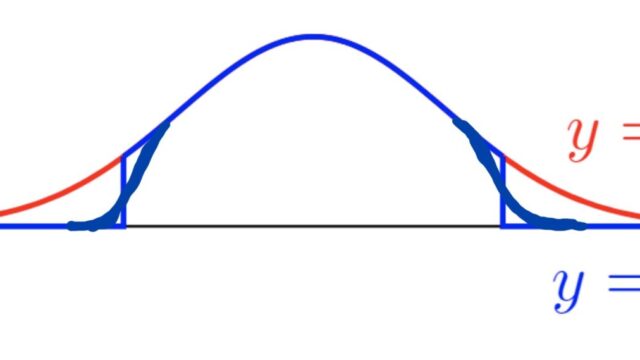 関数解析学
関数解析学 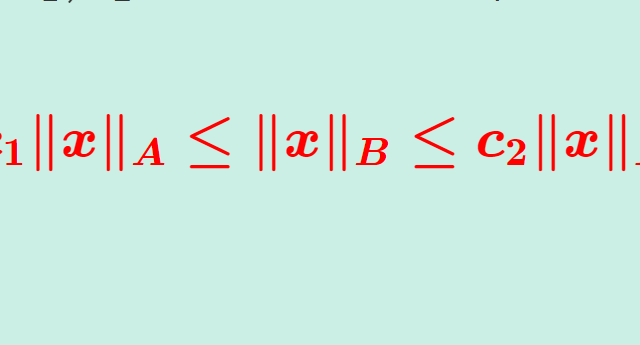 関数解析学
関数解析学 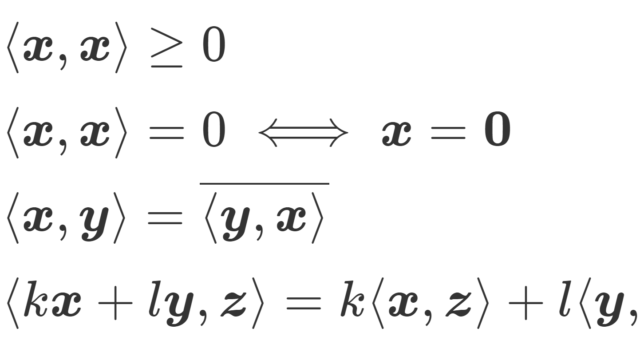 関数解析学
関数解析学 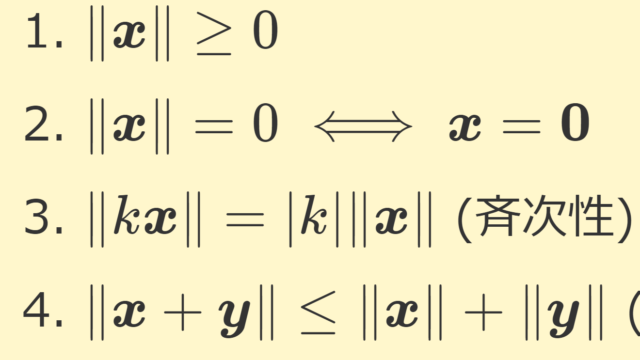 関数解析学
関数解析学