 線形代数学
線形代数学 行列のトレース(tr)とは~定義と性質とその証明~
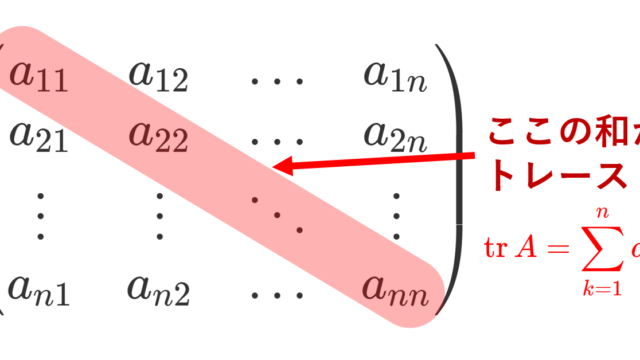
正方行列に対して定義されるトレース(trace, 跡)とは,対角成分の和を指します。これについて,定義を図を交えて整理し,さらにその性質(線形性・可換,相似不変性・固有値との関係・可換性のある線形汎関数は固有値に限る)を証明しましょう。
 線形代数学
線形代数学  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学) 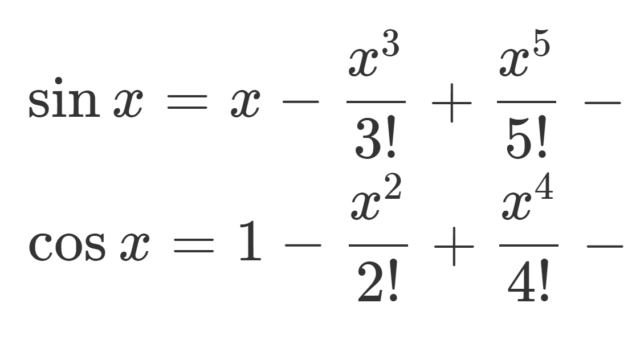 微分積分学(大学)
微分積分学(大学) 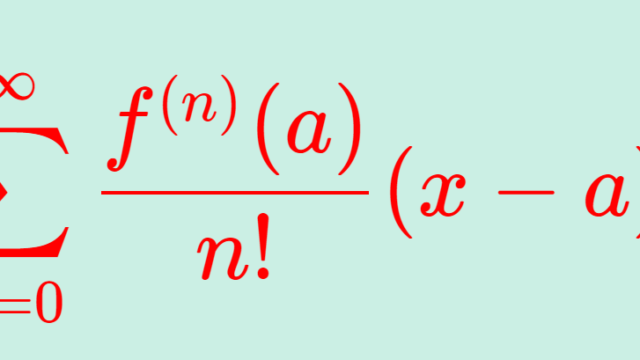 微分積分学(大学)
微分積分学(大学)  線形代数学
線形代数学 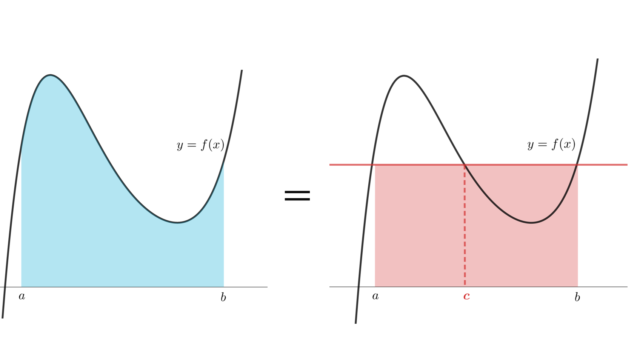 微分積分学(大学)
微分積分学(大学) 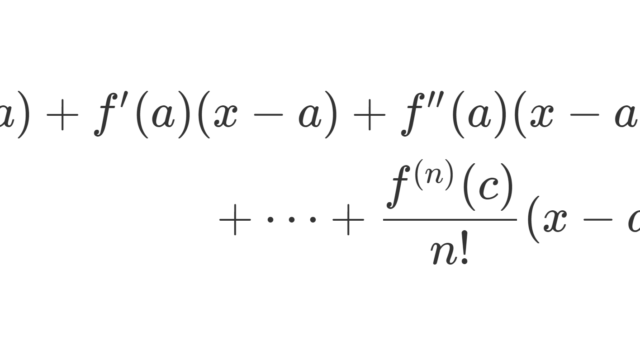 微分積分学(大学)
微分積分学(大学) 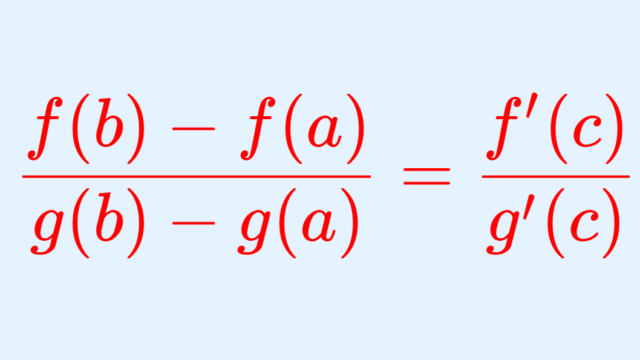 微分積分学(大学)
微分積分学(大学)