 集合と位相
集合と位相 【位相空間】稠密性と可分性~定義と具体例11個~
位相空間の部分集合が,稠密(ちゅうみつ)であるとは,閉包が全体集合に一致することを言い,可分であるとは,高々可算な稠密部分集合を持つ位相空間のことを言います。稠密の定義と可分の定義を,それぞれたくさんの具体例を添えて確認していきましょう。
 集合と位相
集合と位相  集合と位相
集合と位相 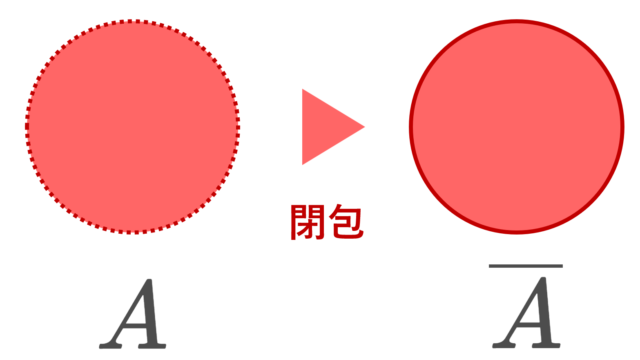 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  記号・記法
記号・記法  解析学(大学)その他
解析学(大学)その他