 確率論
確率論 【確率論】チェビシェフの不等式とその例題・証明
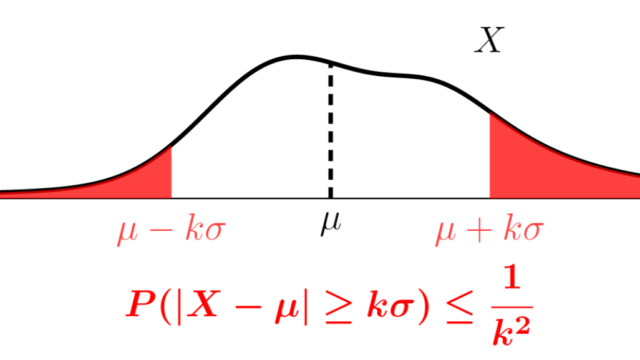
チェビシェフの不等式 ( Chebyshev's inequality) とは,裾の確率を上から評価する不等式を指します。これについて,例題や証明を理解していきましょう。証明にはマルコフの不等式を用います。
 確率論
確率論  群・環・体
群・環・体  群・環・体
群・環・体  群・環・体
群・環・体  群・環・体
群・環・体 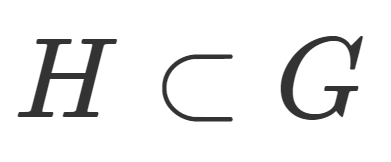 群・環・体
群・環・体 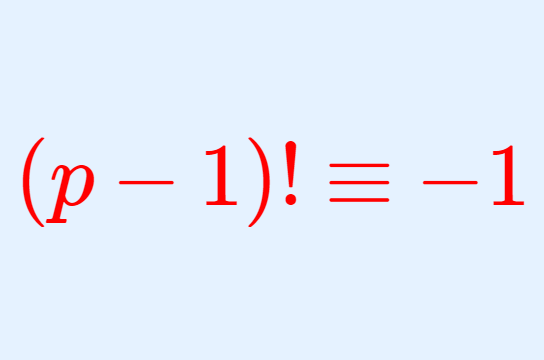 数論
数論 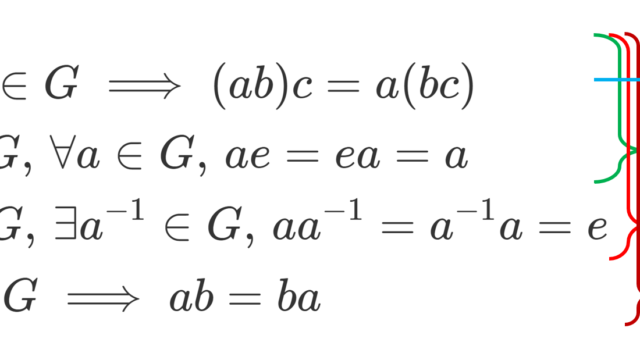 群・環・体
群・環・体 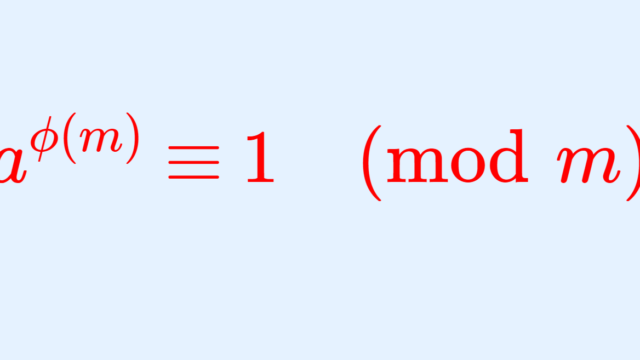 数論
数論  数論
数論