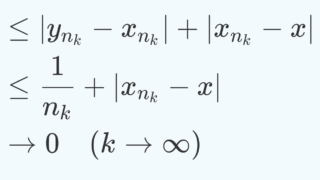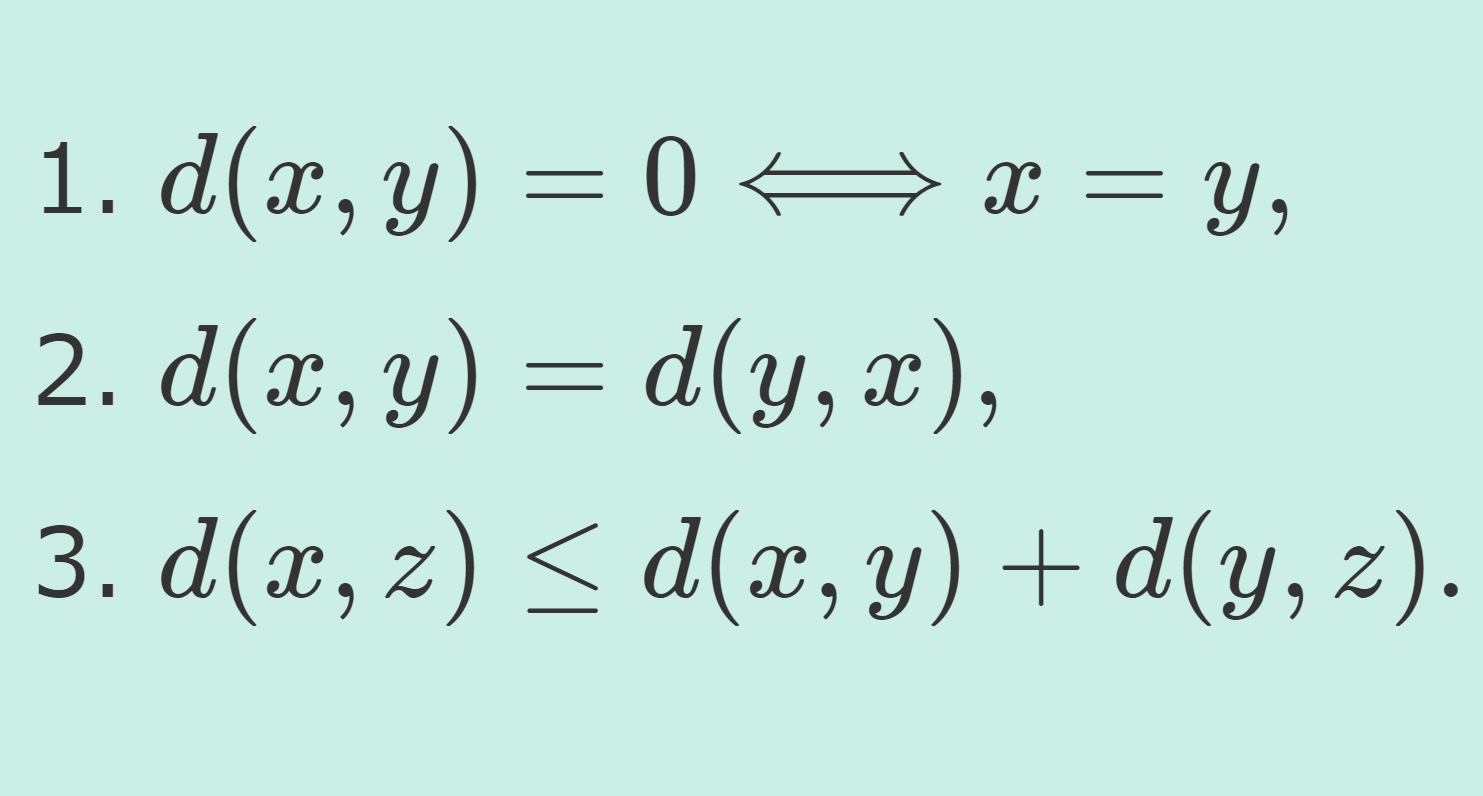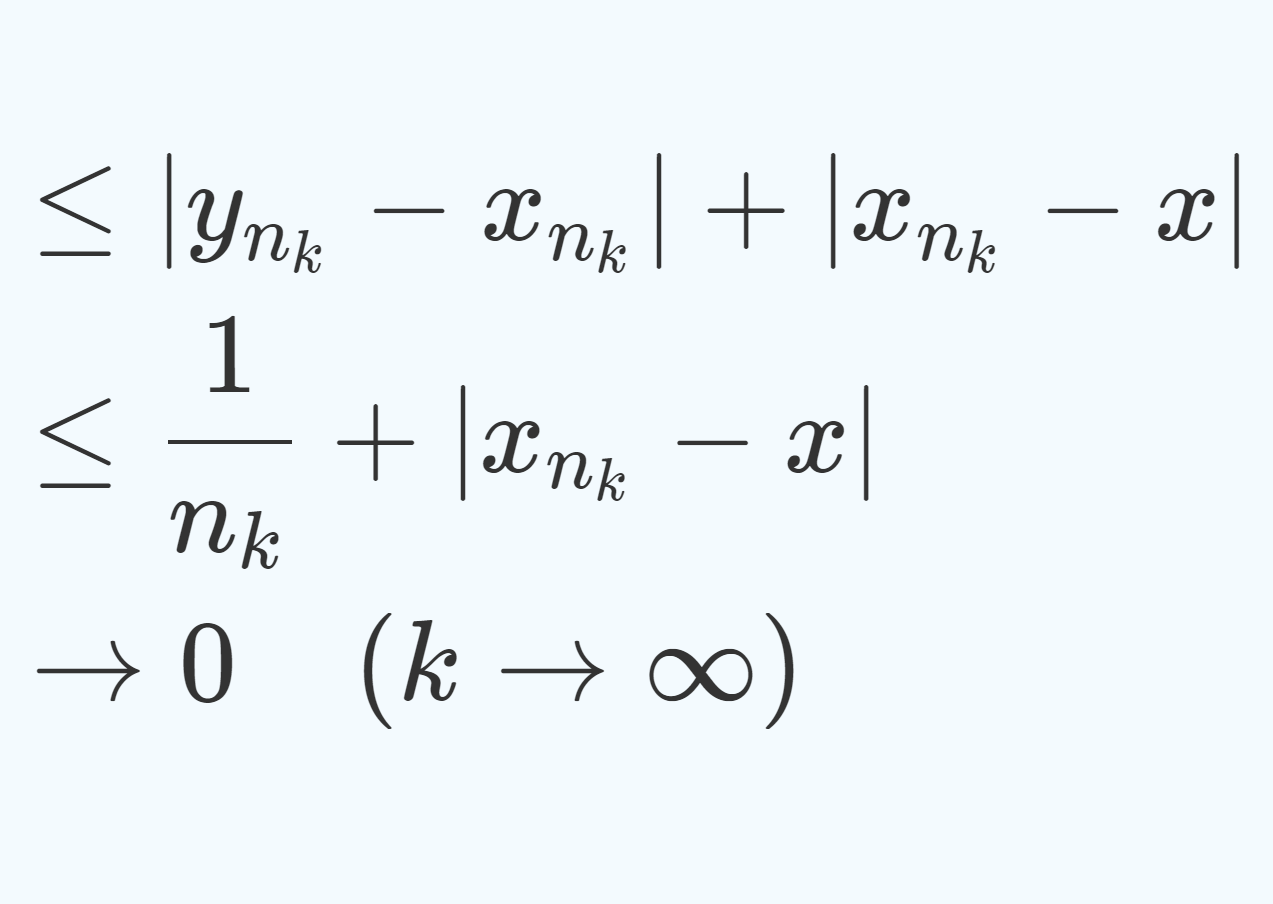一様連続性とは,集合の上における,各点での連続性より強い概念です。
連続性と一様連続性の違いを,図や具体例を交えて詳しく確認していきましょう。
一様連続と連続の定義
まずは今回の主役である「一様連続」を定義し,そのあとに単なる「連続」の定義も復習しましょう。
以下, f\colon A \to \mathbb{R} とします。
定義(一様連続)
f が A 上一様連続 (uniformly continuous) であるとは,
\textcolor{red}{\lim_{\delta\to 0+}\sup_{|x-y|<\delta} |f(x) - f(y)| = 0}が成立すること,すなわち,任意の \varepsilon > 0 に対して,ある(\varepsilon にしか依存しない) \delta > 0 が存在して,
|x-y|<\delta, \,x,y\in A \Longrightarrow |f(x)-f(y)| < \varepsilonが成立することである。
定義(連続)
f が A 上連続 (continuous) であるとは,
\textcolor{red}{\lim_{x\to a} f(x) = f(a), \quad a \in A }が成立すること,すなわち,任意の \varepsilon > 0, a \in A に対して,ある ( \varepsilon と a に依存する) \delta > 0 が存在して,
|x-a|<\delta, \, x \in A \Longrightarrow |f(x)-f(a)| < \varepsilonが成立することである。
定義から,「一様連続 \Longrightarrow 連続」が従います。
「一様連続」とは,各点 a \in A によらず「一様に」,すなわち「全体的に均一に」連続であると言っています。
ここでいう,「全体的に均一」とは,「変化による差が」全体的に均一であることを意味します。
以下に,図を交えてまとめておきましょう。
- 一様連続とは,「変化による差」が”全体的に一様”に0に近づく
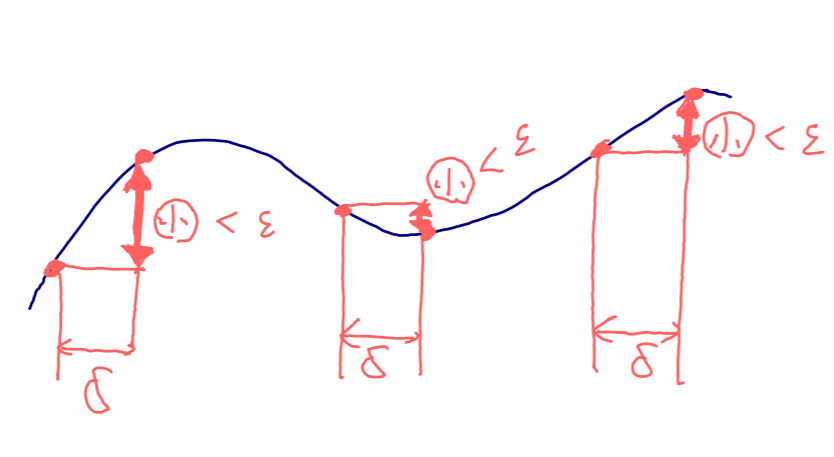
- 単なる「連続」とは各点で見て,「変化による差」が0に近づく。”全体に一様”とは限らない
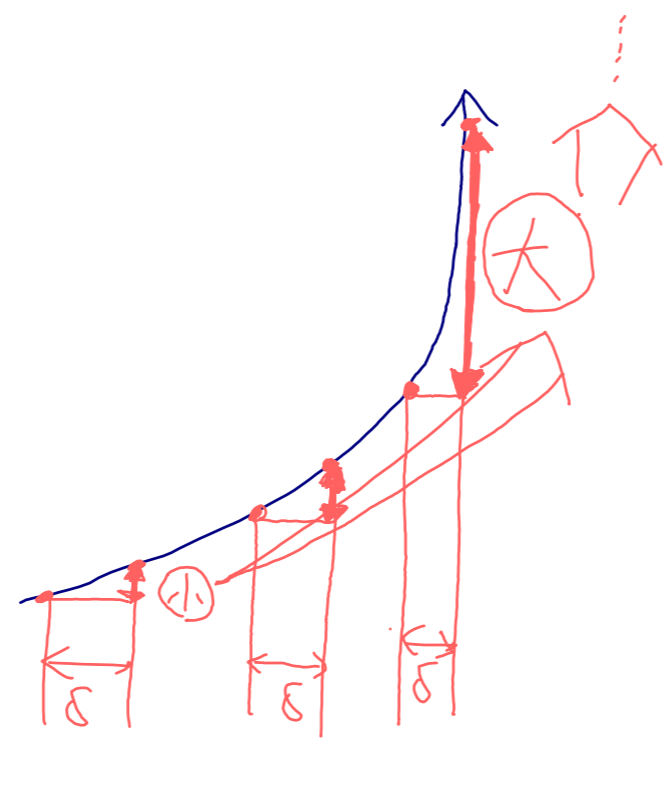
一様連続と連続の具体例
さて,具体例を確認することで,イメージを膨らませていきましょう。
例1.
\textcolor{red}{f(x) = x^2} は, [0,1] 上一様連続である。
一方, [0, \infty) 上連続だが,一様連続ではない。
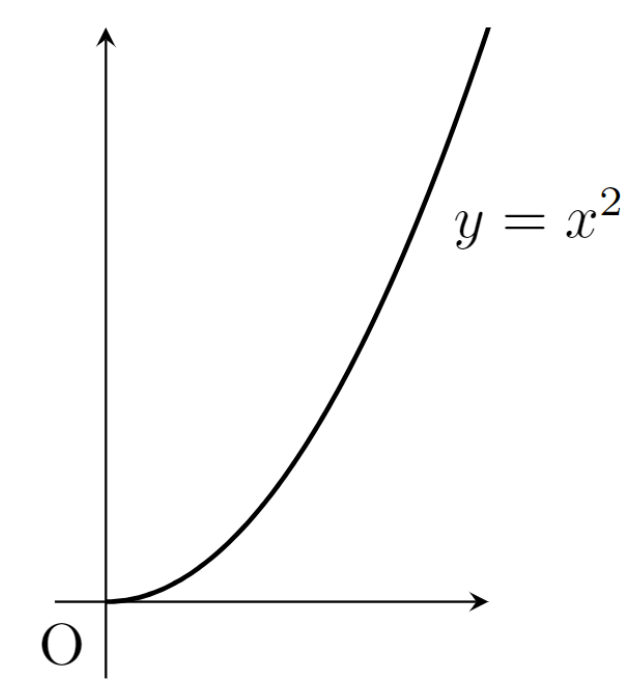
図を見ると, \infty にいくほど,「変化差」が大きくなっていくのがわかるでしょう。 [0,1] 区間に区切って,無限遠を考えないことにすれば,「変化差」が大きくなりすぎないため,一様連続になります。
一方, [0, \infty) まで拡張すると,無限遠の方で「変化差」が大きくなりすぎるため,均一には抑えられず,一様連続にはなりません。
例2.
\textcolor{red}{f(x) = \sqrt{x}} は, [0, \infty) 上一様連続である。
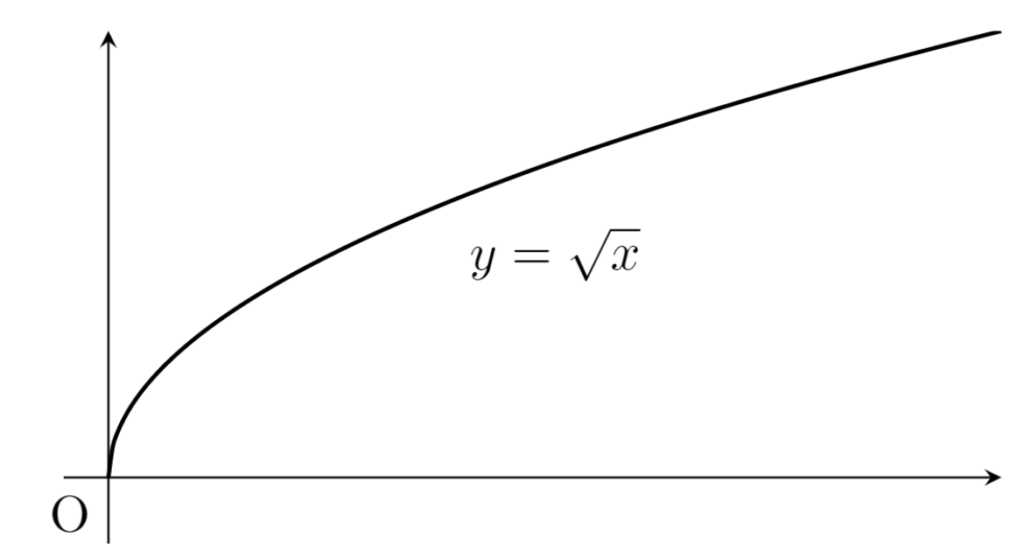
図を見ると,「変化差」は原点付近で一番大きく,遠くに行っても大きくならないことが分かります。よってこれは [0, \infty) 上一様連続になります。
実際, \sup_{|x-y|<\delta} |\sqrt{x} - \sqrt{y}|= \sqrt{\delta} \xrightarrow{\delta \to 0+} 0 なので,一様連続であることが分かります。
例3.
\textcolor{red}{f(x) = \tan x} は, (-\pi/2, \pi/2) 上連続だが,一様連続ではない。
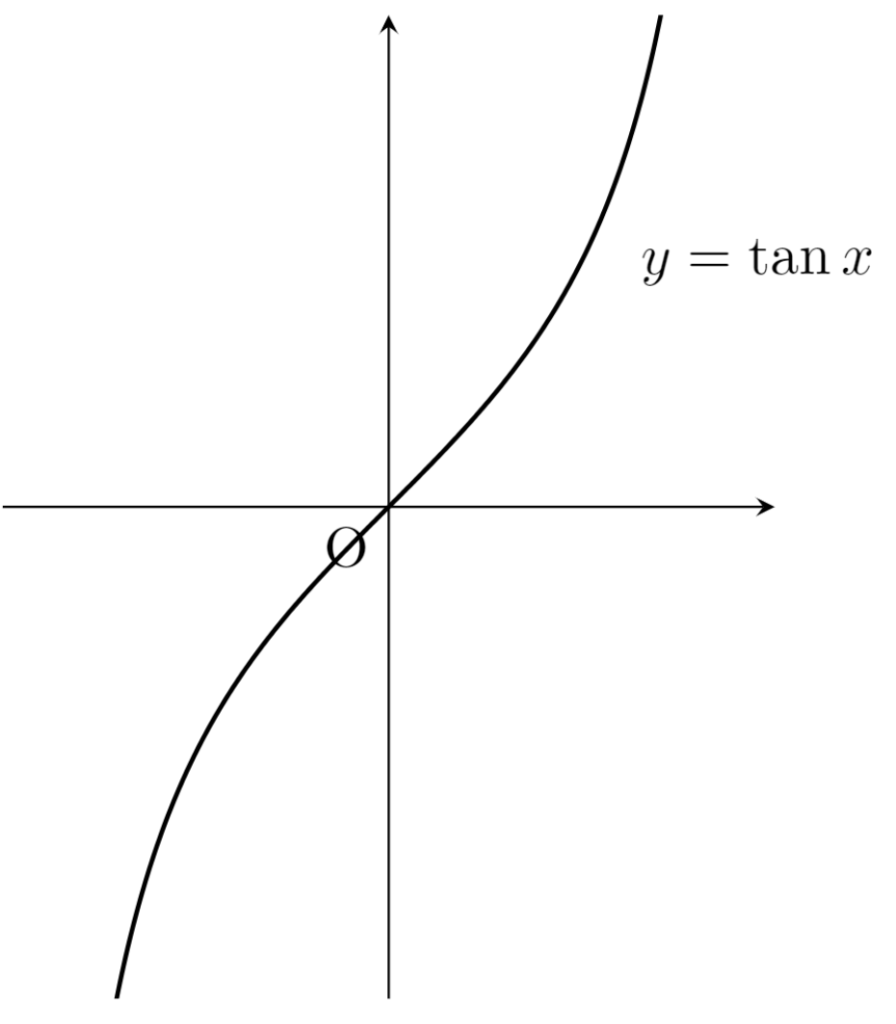
図を見ると,「変化差」は \pm \pi / 2 付近でどんどん大きくなっていくことが分かります。よって,これは (-\pi/2, \pi/2) 上一様連続ではありません。
例4.
\textcolor{red}{f(x) = \sin (1/x) } は, (0, 1) 上連続だが,一様連続ではない。
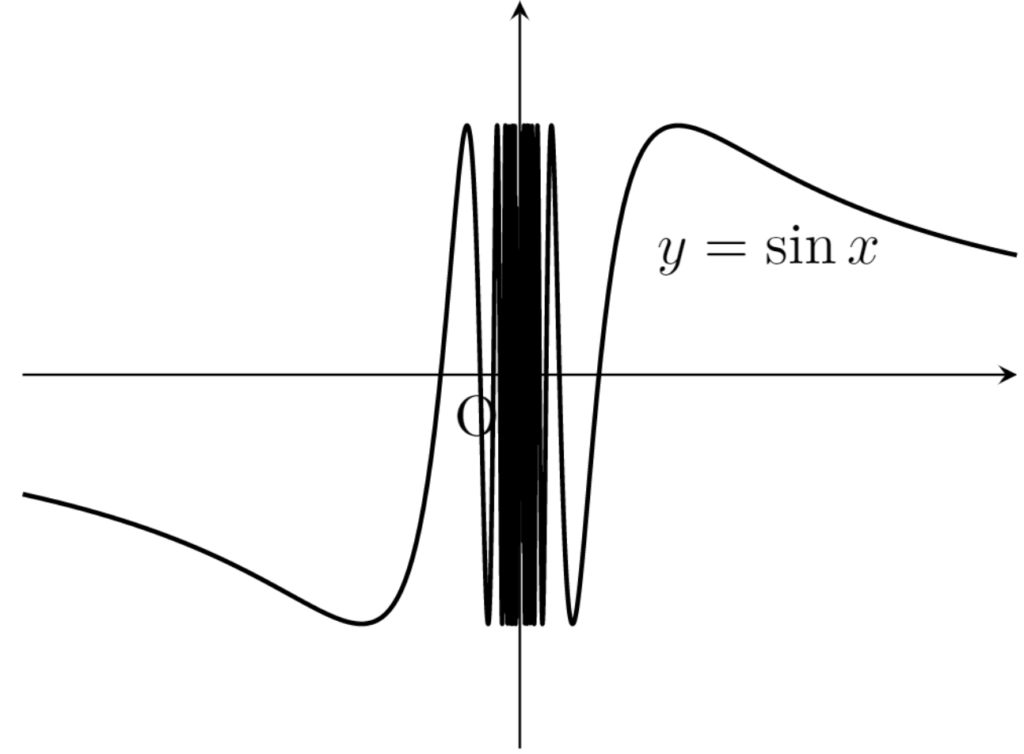
図を見ると,「変化差」は原点付近でどんどん大きくなっていくことが分かります。よって,これは (0, 1) 上一様連続ではありません。
一様連続に関する有名な定理
最後に,一様連続に関する有名な定理を一つ紹介しましょう。
定理
有界閉区間上の連続関数は一様連続である。
有界閉区間上であれば,「連続」ならばより強い「一様連続」が従うという定理です。「有界」であることと,「閉」であることが大切です。
これの証明については,下の記事を見てください。