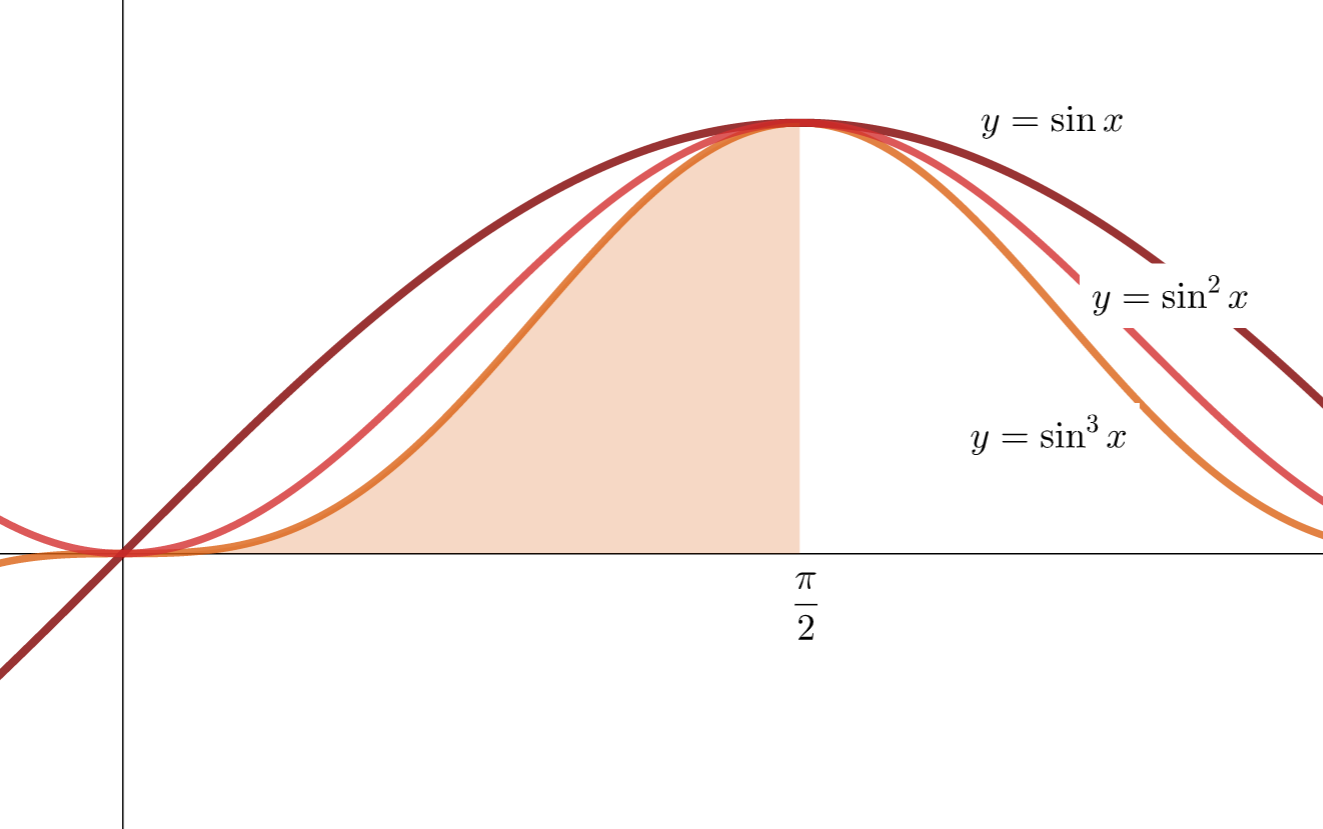
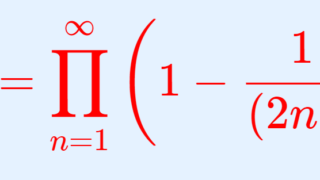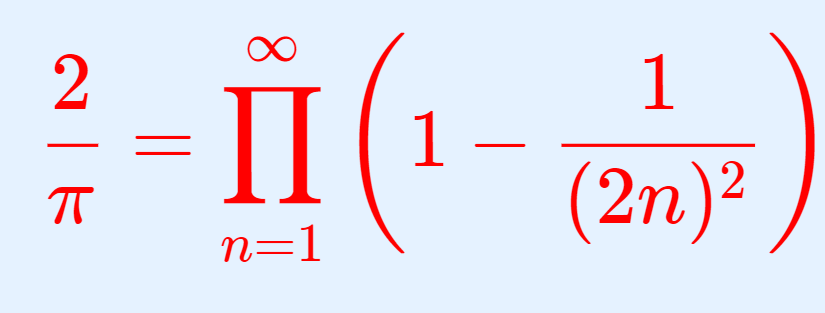ウォリス積分,またはワリス積分と呼ばれる積分 \int_0^{\pi/2} \sin^n x \, dx, \, \int_0^{\pi/2} \cos^n x \, dx について,その導出と性質を紹介しましょう。証明は理系高校生でも理解できるものです。
【ウォリス積分】sin,cosのn乗積分に関する定理
定理(ウォリス積分, Wallis integral)
n \ge 0 に対し,
\color{red} \begin{aligned} &\int_0^{\frac{\pi}{2}} \sin^n x \, dx = \int_0^{\frac{\pi}{2}} \cos^n x \, dx \\ &=\begin{dcases} \frac{(n-1)!!}{n!!} & \text{if } n \text{ is odd,}\\[10pt] \frac{\pi}{2}\frac{(n-1)!!}{n!!} & \text{if }n \text{ is even.}\end{dcases}\\[30pt] &=\begin{dcases} \frac{2^{2k} (k!)^2}{(2k+1)(2k)!} & \text{if }n = 2k+1,\\[10pt] \frac{\pi}{2}\frac{(2k)!}{2^{2k} (k!)^2} & \text{if }n =2k. \end{dcases} \end{aligned}
ただし, \text{odd, even} はそれぞれ奇数・偶数の英語である。また,2重階乗
\small n!! =\begin{cases} n(n-2)(n-4) \dots 3 \cdot 1 & \text{if } n \text{ is odd,} \\ n(n-2)(n-4) \dots 4 \cdot 2 & \text{if } n \text{ is even,} \end{cases}
0!! =(-1)!! = 1 を用いた。
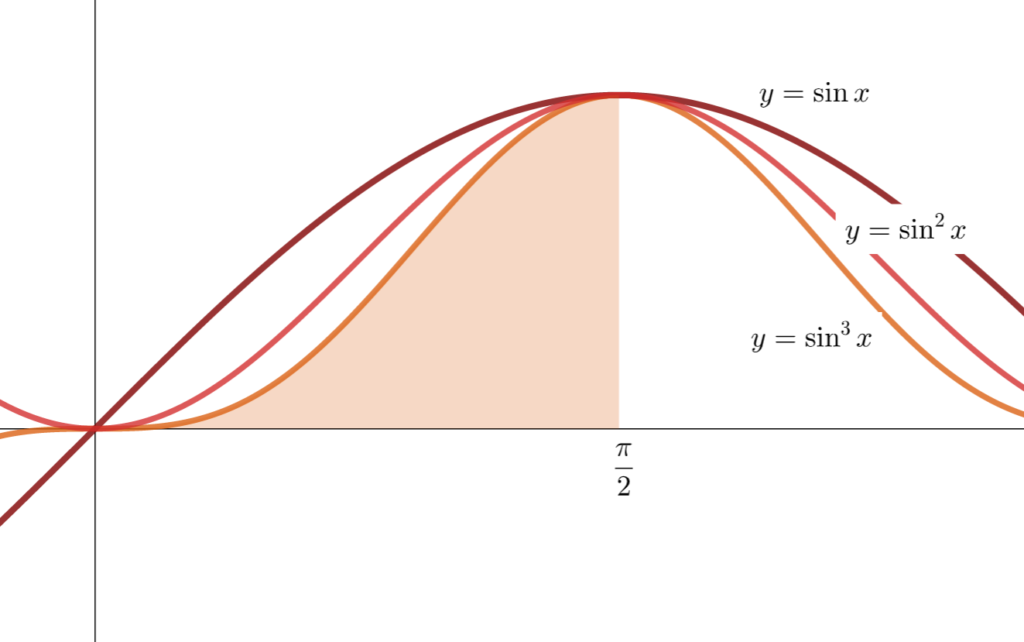
なお,最初の等式 \displaystyle \int_0^{\frac{\pi}{2}} \sin^n x \, dx = \int_0^{\frac{\pi}{2}} \cos^n x \, dx については,ほぼ自明でしょう。実際 \sin x = \cos(\pi/2 - x) であるため,置換積分により,
\begin{aligned} \int_0^{\frac{\pi}{2}} \sin^n x \, dx &= \int_0^{\frac{\pi}{2}} \cos^n \left(\frac{\pi}{2} - x\right) \, dx\\ &= \int_0^{\frac{\pi}{2}} \cos^n y \, dy\end{aligned}
となることがわかります。
【ウォリス積分】sin,cosのn乗積分の導出
それでは,
\color{red} \begin{aligned} &\int_0^{\frac{\pi}{2}} \sin^n x \, dx \\ &=\begin{dcases} \frac{(n-1)!!}{n!!} & \text{if } n \text{ is odd,}\\ \frac{\pi}{2}\frac{(n-1)!!}{n!!} & \text{if }n \text{ is even.}\end{dcases}\\ &=\begin{dcases} \frac{2^{2k} (k!)^2}{(2k+1)(2k)!} & \text{if }n = 2k+1,\\ \frac{\pi}{2}\frac{(2k)!}{2^{2k} (k!)^2} & \text{if }n =2k. \end{dcases} \end{aligned}
の証明を行いましょう。
証明
I_n = \int_0^{{\pi}/{2}} \sin^n x \, dx とおく。特に,
\begin{aligned} I_0 &= \int_0^{\frac{\pi}{2}} \, dx =\frac{\pi}{2}, \\ I_1 &= \int_0^{\frac{\pi}{2}}\sin x \, dx = [-\cos x]_0^\frac{\pi}{2} = 1 \end{aligned}
となる。ここで,部分積分により n \ge 2 のとき
従って, I_n =\dfrac{n-1}{n} I_{n-2} である。これにより,
\begin{aligned} I_n &= \frac{n-1}{n} I_{n-2} \\ &= \frac{n-1}{n} \frac{n-3}{n-2} I_{n-4}\\ &= \cdots \\ &=\frac{(n-1)!!}{n!!} \times \begin{cases} I_1 &\text{if } n \text{ is odd,} \\ I_0 &\text{if } n \text{ is even.} \end{cases}\\ &= \begin{cases} \frac{(n-1)!!}{n!!} & \text{if } n \text{ is odd,}\\ \frac{\pi}{2}\frac{(n-1)!!}{n!!} & \text{if } n \text{ is even.}\end{cases} \end{aligned}
を得る。後半は
からわかる。
証明終
ウォリス積分の性質
ウォリス積分の性質を挙げておきましょう。
ウォリス積分の基本的な性質
定理(ウォリス積分の性質)
- m<n が非負整数のとき,
\int_0^{\frac{\pi}{2}} \sin^m x \, dx > \int_0^{\frac{\pi}{2}} \sin^n x \, dx. - \lim_{n\to\infty} \int_0^{\frac{\pi}{2}} \sin^n x \, dx =0.
証明しておきます。
証明
1. \int_0^{\frac{\pi}{2}} \sin^m x \, dx > \int_0^{\frac{\pi}{2}} \sin^n x \, dx について
\sin^m x < \sin^n x \,\,(0 < x< \pi/2) であり,かつどちらも連続であるから,積分についても \int_0^{\frac{\pi}{2}} \sin^m x \, dx >\int_0^{\frac{\pi}{2}} \sin^n x \, dx.
2. \lim_{n\to\infty} \int_0^{\frac{\pi}{2}} \sin^n x \, dx =0 について
I_n = \int_0^{{\pi}/{2}} \sin^n x \, dx とおく。1.より, \{I_n\} は非負かつ単調減少であるから,収束先が存在する。よって, \alpha = \lim_{n\to\infty} I_n としよう。ウォリス積分の公式により,
\begin{aligned} I_n I_{n+1}&= \frac{\pi}{2} \frac{(n-1)!!}{n!!}\frac{n!!}{(n+1)!!} \\ &= \frac{\pi}{2}\frac{n!}{(n+1)!} \\ &= \frac{\pi}{2} \frac{1}{n+1} \end{aligned}
であるから,両辺 n\to\infty とすると, \alpha^2 = 0 であり,結局 \alpha=0 となる。
証明終
2.については,極限と積分の交換ができて,
\begin{aligned} \lim_{n\to\infty} \int_0^{\frac{\pi}{2}} \sin^n x \, dx &=\int_0^{\frac{\pi}{2}}\lim_{n\to\infty} \sin^n x \, dx \\ &= \int_0^{\frac{\pi}{2}}0 \, dx \\ &=0. \end{aligned}
でも証明可能です。
ウォリスの公式
ウォリス積分を用いることで,「ウォリスの公式」と呼ばれる,以下の公式を証明することが可能です。
定理(ウォリスの公式; Wallis formula)
\small \color{red} \begin{aligned}\sqrt{\pi} &= \lim_{n\to\infty} \frac{1}{\sqrt{n}} \frac{(2n)!!}{(2n-1)!!} =\lim_{n\to\infty} \frac{2^{2n}}{\sqrt{n}}\frac{(n!)^2}{(2n)!}, \\ \frac{\pi}{2} &= \prod_{n=1}^\infty \frac{(2n)^2}{(2n-1)(2n+1)} = \frac{2^2}{1\cdot 3}\cdot \frac{4^2}{3\cdot 5} \cdots ,\\ \frac{2}{\pi}&= \prod_{n=1}^\infty \left( 1-\frac{1}{(2n)^2}\right) = \left(1-\frac{1}{2^2}\right) \left(1-\frac{1}{4^2}\right)\cdots. \end{aligned}これについての解説は,以下の記事で行っています。