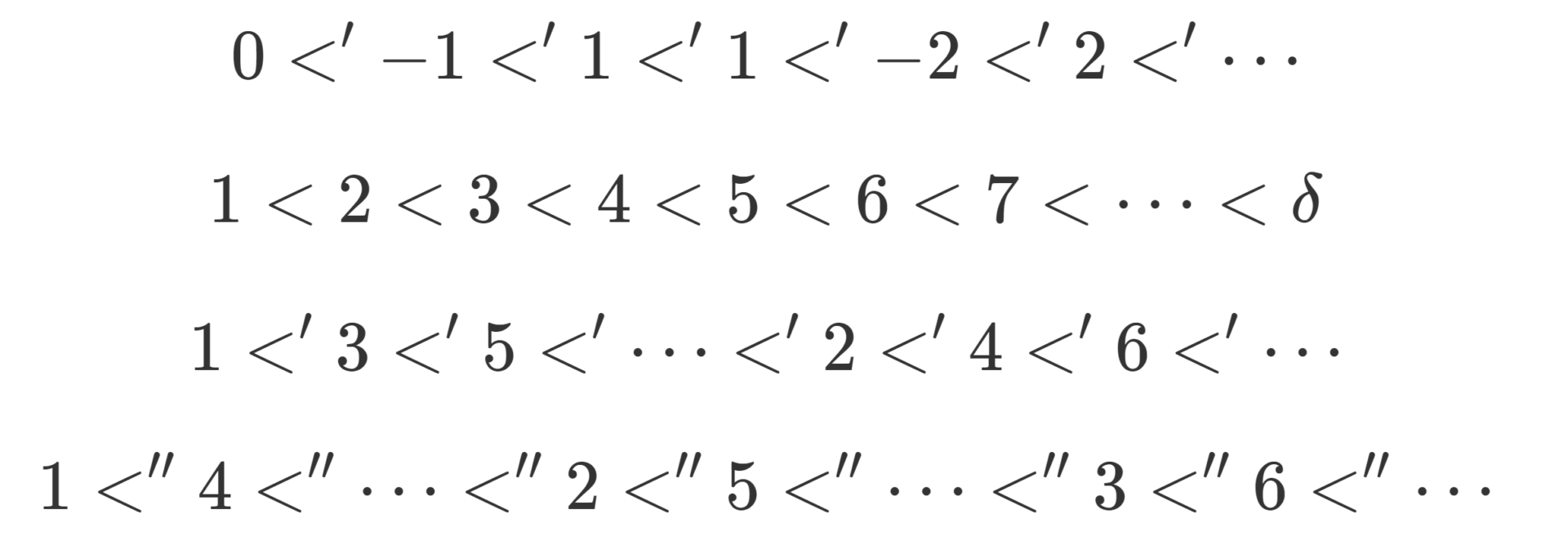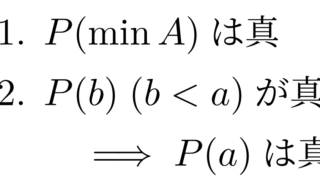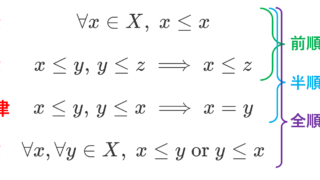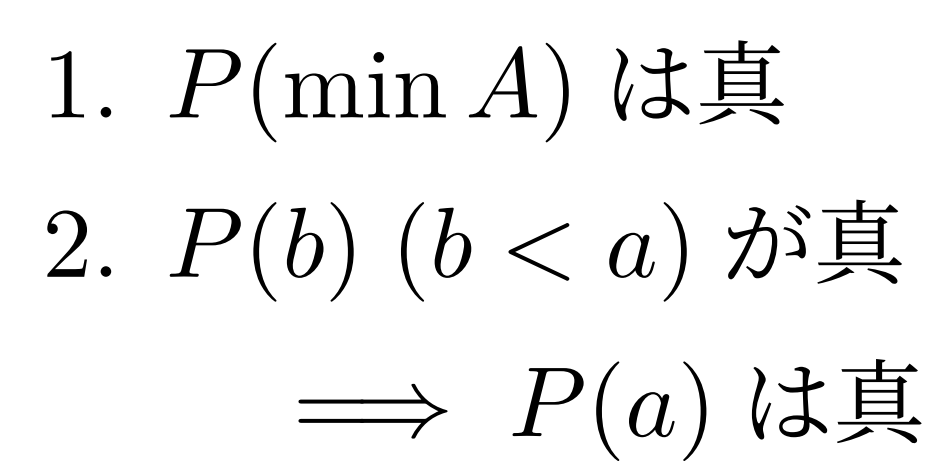整列集合とは,「間隔を空けてきれいに順番に並んだ」集合のことで,具体的には,どんな部分集合を持ってきてもちゃんと大小関係として最小値が定まるような順序集合のことを言います。
整列集合の定義と,重要な性質を証明し,さらに選択公理と同値で驚愕の定理である,整列可能定理を紹介しましょう。
整列集合とは~定義と例~
まずは定義と例を紹介し,感覚をつかみましょう。
整列集合の定義

定義1(整列集合)
半順序集合 A に対し,任意の空でない部分集合が最小値を持つとき,整列集合 (well-ordered set) という。
「半順序集合」といいましたが,任意の2元が最小値を持つことから,整列集合は全順序集合です。半順序集合・全順序集合については以下の図が分かりやすいと思います(→半順序集合・全順序集合の定義・具体例4つとその周辺)。
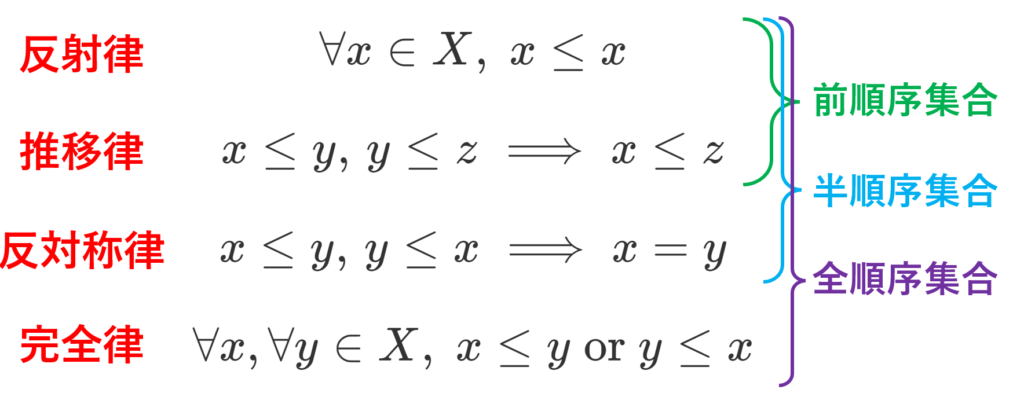
整列集合の例・そうでない例
整列集合の例・そうでない例を述べることで感覚をつかみましょう。
整列集合の例・そうでない例1.
- \mathbb{N}=\{1,2,3,\dots\} は通常の順序で整列集合である。
- \mathbb{Z}=\{ \dots, -2,-1,0,1,2,\dots\} は通常の順序で整列集合でない。
- 実数全体の集合 \mathbb{R} や非負の数全体の集合 \mathbb{R}_{\ge 0} は通常の順序で整列集合でない。
1.については,どんな部分集合を持ってきても最小値が取れるため,整列集合です。2.について,集合 \mathbb{Z} はそもそも最小値を持たないため,整列集合ではありません。3.も同様で,たとえば正の数全体の集合 \mathbb{R}_{>0}\subset \mathbb{R}_{\ge 0},\mathbb{R} は最小値を持たないため,整列集合ではありません。
整列集合の例2.
\mathbb{Z} 上の a,b\in\mathbb{Z} に対し, |a|<|b| のとき a<' b とし, |a|=|b| のとき通常の大小を採用した順序
0<' -1 <' 1<' 1<' -2<' 2<'\cdots
は整列順序であり,これにより (\mathbb{Z},\le') は整列集合になる。
\mathbb{Z} そのものは整列集合ではありませんが,順序の入れ方を変えることで整列集合にできます。
整列集合の例3.
\mathbb{N} に \delta を追加した集合 \mathbb{N}\cup \{\delta\} に,正の整数同士は通常の大小関係を採用し, a\in\mathbb{N} に対し常に a<\delta となるような順序
1<2<3<4<\dots < \delta
は整列順序であり,これにより (\mathbb{N}\cup \{\delta\}, \le ) は整列集合になる。
この例は整列集合の例として非常に大切です。任意の部分集合がちゃんと最小値を持つことを確認してください。このように,「間」に無限個の数が入るような整列順序の定め方もあります。
以下の2つも大切な例です。
整列集合の例4.
\mathbb{N} 上の a, b\in\mathbb{N} に対し, a,b の偶奇が一致していれば通常の大小を採用し, a が奇数, b が偶数なら a<'b として定めた順序
1<'3<'5<' \dots <' 2<' 4<' 6<'\cdots
は整列順序であり,これにより (\mathbb{N},\le') は整列集合になる。
整列集合の例5.
\mathbb{N} 上で, 3 で割った余りに着目して定めた順序
\begin{aligned}&1<''4<''7<'' \cdots \\ &\quad<'' 2<'' 5<'' 8<'' \cdots\\&\qquad<'' 3<''6<''9<''\cdots\end{aligned}
は整列順序であり,これにより (\mathbb{N},\le'') は整列集合になる。
整列集合の性質
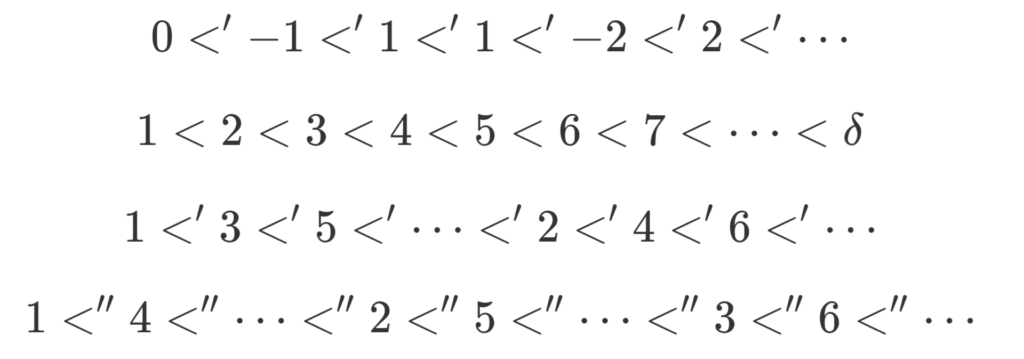
まずは整列集合の性質を述べる際に用いる,整列集合の切片について定義しておきましょう。
定義2(整列集合の切片)
整列集合 X に対し,
\Large \color{red}X\langle a\rangle =\{ x\in X\mid x<a\}
を X の元 a による切片 (section) という。
明らかに切片も整列集合であり, a\le b\iff X\langle a\rangle \subset X\langle b\rangle , a\le b なら (X\langle b\rangle)\langle a\rangle=X\langle a\rangle です。
また, a=\min X とするとき, X\langle a\rangle =\emptyset ですが,これも切片と考えます。
1. 順序を保つ単射と整列集合
定理1(順序を保つ単射と整列集合)
X が整列集合で, f\colon X\to X が順序を保つ単射であれば,常に \large \color{red} f(x)\ge x が成り立つ。
順序を保つ写像 (order-preserving) とは, x\le y\implies f(x)\le f(y) が成り立つことをいいます。特に今は単射なので, x< y\implies f(x)< f(y) が成り立ちます。
証明
A=\{x\in X\mid f(x)<x\} とすると, A=\emptyset を示せばよい。 A\ne \emptyset とすると,整列集合の定義より a=\min A が存在する。
f(a)<a であり, f は順序を保つ単射なので f(f(a))<f(a) が成り立つ。よって f(a)\in A だが, a の最小性に矛盾する。
証明終
2. 整列集合とその切片の順序同型
半順序集合 X と Y が順序同型 (order isomorphic) である (\large \color{red} X\simeq Y とかく)とは,順序を保つ全単射 f\colon X\to Y が存在することを言います。
定理2(整列集合とその切片の順序同型)
X,Y を整列集合とする。このとき,
- 任意の a\in X に対し, X\not\simeq X\langle a\rangle である。また, a\ne b\in X なら X\langle a\rangle \not\simeq X\langle b\rangle である。
- X\simeq Y なら,順序同型写像 f\colon X\xrightarrow{\simeq} Y の取り方は一意的である。また,このとき,任意の a\in X に対し X\langle a\rangle\simeq Y\langle f(a)\rangle である。
証明
1.について 前半について f\colon X\simeq X\langle a\rangle とすると, f(a)\in X\langle a\rangle より, f(a)<a となって定理1に矛盾する。後半は a>b とすると X\langle b\rangle =(X\langle a\rangle)\langle b\rangle であるから, X\langle a\rangle を X と思い直すことで前半に帰着する。
2.について 後半は簡単で, f\colon X\simeq Y とすると,明らかに f(X\langle a\rangle )=Y\langle f(a)\rangle よりわかる。前半について, f,g\colon X\simeq Y とすると,後半より a\in X について Y\langle f(a)\rangle \simeq Y\langle g(a)\rangle である。1.の後半より, f(a)=g(a) であるから, f=g である。
証明終
3. 整列集合の比較定理
次の定理は非常に有用で,整列集合の凄さを表している定理だと思います。
定理3(整列集合の比較定理)
X,Y を空でない整列集合とするとき,以下のいずれか一つのみが必ず成立する。
- X\simeq Y
- ある a\in X が存在して, X\langle a\rangle \simeq Y
- ある b\in Y が存在して, X\simeq Y\langle b\rangle
たとえば,整列集合の例2.で紹介した (\mathbb{Z},\le'),すなわち
0<' -1 <' 1<' 1<' -2<' 2<'\cdots
は整列集合 (\mathbb{N},\le),すなわち
と順序を保つ全単射が作れるので, (\mathbb{Z},\le')\simeq (\mathbb{N},\le) です。また,整列集合の例4.で紹介した (\mathbb{N},\le'),すなわち
と,通常の順序による整列集合 (\mathbb{N},\le) とは, (\mathbb{N}\langle 2\rangle ,\le' )\simeq (\mathbb{N},\le) になります。
証明
\begin{aligned} X_1&=\{ a\in X\mid \exists b\in Y, \,X\langle a\rangle \simeq Y\langle b\rangle\} \\ Y_1&=\{ b\in Y\mid \exists a\in X, \,X\langle a\rangle \simeq Y\langle b\rangle\} \end{aligned}
と定める。まず, X_1\simeq Y_1 を示そう。
a\in X_1 とすると, X_1 の定義から X\langle a\rangle \simeq Y\langle b\rangle となる b\in Y が存在し,特に b\in Y_1 である。また定理2.1より,このような b は一意で,写像 \varphi \colon X_1\ni a\mapsto b \in Y_1 は順序同型写像である。 X_1=\emptyset のときは明らかに Y_1=\emptyset となるので赤字は示せた。
X_1\subset X は X そのものあるいは X のある切片となることを示そう。
X_1=\emptyset \text{ or } X のときはよい。そうでないとき, a\in X_1 とすると,ある b\in Y があって f\colon X\langle a\rangle \simeq Y\langle b\rangle とできる。定理2.2より, x\in X\langle a\rangle に対し X\langle x\rangle \simeq Y\langle f(x)\rangle とできるため, X\langle a\rangle \subset X_1 である。
a_1=\min X\setminus X_1 とする。 a_1 の定義より, X\langle a_1\rangle\subset X_1 かつ a_1\notin X_1 である。 a_2\in X_1\setminus X\langle a_1\rangle とすると,その取り方から a_2>a_1 であり, a_2\in X_1 と前半の議論より a_1\in X \langle a_2\rangle\subset X_1 となってしまって a_1\notin X_1 に矛盾する。この矛盾は a_2 の存在を仮定したことから来るものなので, X_1=X\langle a_1\rangle なので青字は示せた。
最後に定理を示そう。 Y_1 も同様に Y そのものか Y の切片となる。もし, X_1=X\langle a\rangle かつ Y_1=Y\langle b\rangle とすると,赤字より
X\langle a\rangle=X_1\simeq Y_1=Y\langle b\rangle
となって, a\in X_1 となるが,これは a\notin X\langle a\rangle =X_1 に矛盾している。よって, X_1=X または Y_1=Y のいずれかは成り立つため,定理3の1.~3.のいずれか一つは成り立つ。
いずれか一つ「のみ」成り立つことは,定理2.1から明らか。
証明終
4. 超限帰納法
整列集合の重要な定理の一つに,超限帰納法というものがあります。これは,数学的帰納法を一般化したものです。これについては,以下で解説しています。
5. 整列可能定理
以下の定理は,選択公理と同値なツォルンの補題を用いて証明される,驚くべき定理です。
定理5(整列可能定理)
任意の集合は,その上にある順序を定義して整列集合にすることができる。ただし,選択公理は認める。
Zermeloの整列可能定理 (Zermelo’s well-ordering theorem) といわれることもあります。
たとえば,\R は例1.3で確認したとおり整列集合ではないですが,上手く順序を定めることで整列集合にできるということです。ただし,選択公理が必要なことからもわかる通り,具体的に構成することはできません。
厳密な証明をすると,本質的でない部分で長くなってしまうため,今回は証明のスケッチをするのに留めます。証明は文献[1]を参考にしています。
証明のスケッチ
- X の部分集合 A とその上の整列順序 \le_{\alpha} の組 (A, \le_{\alpha}) 全体の集合を \mathscr{X} とする。
- 整列集合 (A,\le_{\alpha}) が (B,\le_{\beta}) に一致または (B,\le_{\beta}) の切片であるときに限り (A,\le_{\alpha})\le (B,\le_{\beta}) と定義すると, \mathscr{X} は帰納的半順序集合になる。すなわち, \mathscr{Y}\subset \mathscr{X} を全順序部分集合とすると, Y_{\infty}=\bigcup_{(Y, \le_{y})\in\mathscr{Y}} Y も整列集合で,\le に関して \mathscr{Y} における上界になっていることがわかる。
- ツォルンの補題より, \mathscr{X} には極大元 (X', \le_{x'}) が存在する。もし X\ne X' とすると, a\in X\setminus X' として, X'\cup \{ a\} 上に a が一番大きくなるような整列順序を定義できてしまい,極大性に矛盾する。よって X=X' であり, X 上に整列順序を定めることができた。
証明のスケッチ終
さらに,2.の部分の証明の概略は以下です。
2-1. a\in (A,\le_{\alpha}), \, b\in (B, \le_{\beta}), \, (A,\le_{\alpha})\le (B,\le_{\beta}) とすると, a\le b\stackrel{\mathrm{def}}{\iff} a\le_{\beta} b と定めることで, Y_{\infty} 上に順序 \le が定義できる。
2-2. 上で定めた Y_{\infty} 上の順序は整列順序である。 実際, M\subset Y_{\infty} に対し, Y\cap M\ne \emptyset となるような Y\in \mathscr{Y} を一つ取ると,( Y の取り方に依らず) \min M = \min Y\cap M となっていることが証明できる(右辺の存在は Y が整列集合であることからわかる)。
2-3. さらに \mathscr{Y} における任意の整列集合は Y_\infty に一致または Y_\infty の切片になっていることがわかる。
整列可能定理は,選択公理と同値です。整列可能定理を認めると,以下のように簡単に選択公理を証明することができます。
整列可能定理 \implies 選択公理の証明
証明すべきことは,空でない集合族 (A_\lambda)_{\lambda\in\Lambda} に対し, A=\bigcup_{\lambda\in \Lambda} A_\lambda としたときに,写像 f\colon \Lambda\to A で f(\lambda)\in A_\lambda となるものが存在することである(→選択公理の内容と具体例を詳しく)。
整列可能定理より, A は整列集合と思える。すると,単に f(\lambda)=\min A_{\lambda} とすればよい。
証明終
6. 順序数
定理3.より,全ての整列集合はまた「大小比較」できます。順序同型な整列集合を同一視し,その代表元を順序数 (ordinal number) といいます。順序数については,以下で解説しています。