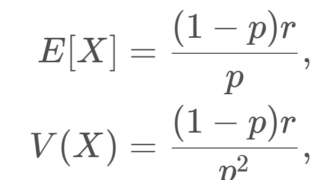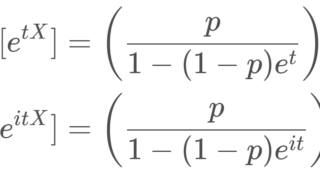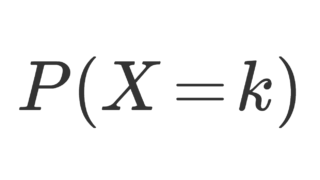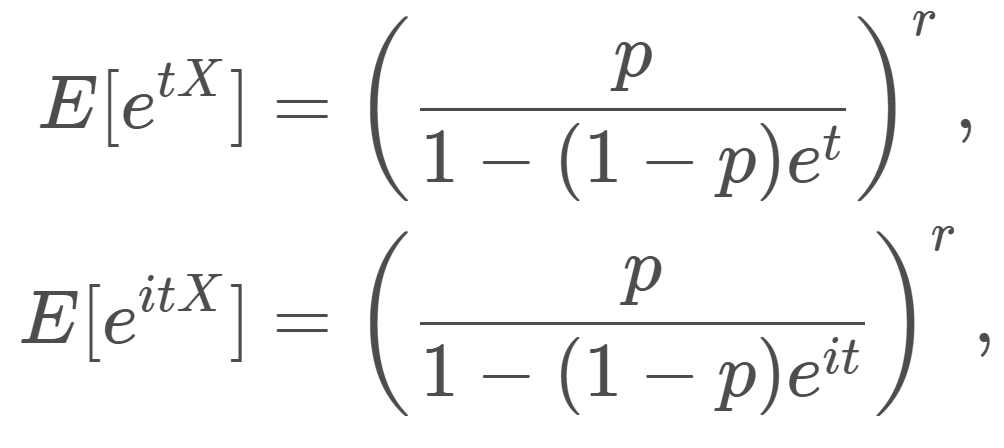コイン投げをしたときの失敗回数を固定し，その失敗回数に到達するまでの成功回数を数える負の二項分布 NB(r, p) は， P(X=k) = {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r となる確率分布です。これについて，その定義と例と性質をまとめましょう。
負の二項分布の定義
定義（負の二項分布）
0<p<1, \, r\ge 1 を整数とする。確率変数 X が k = 0,1,2,\ldots に対し，
\color{red}\begin{aligned} P(X=k) &= {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r \\ &= {}_{k+r-1}\mathrm{C}_{r-1}\, p^k(1-p)^r \end{aligned}
となるとき， X はパラメータ (r, p) の負の二項分布 (negative binomial distribution) に従うという。本記事では，\color{red} X\sim NB(r,p) とかくことにする。
なお，重複組み合わせの記号を用いて，\color{red} {}_{r}\mathrm{H}_k\, p^k(1-p)^r とかいても同様です。本記事では，上の定義の第一等式 {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r のかたちを主に用います。
負の二項分布は，確率 p で表が出るコインについて， r 回ウラが出るまでの表が出る回数を表したものです。
実際，「 r 回ウラが出るまでに， k 回表が出る確率」は，まず最初の r+k-1 回の試行の間に表が k 回，ウラが r-1 回出る確率が {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^{r-1} であり，最後の1回はウラが出るので，確率 1-p で，最終的に
{}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^{r-1} (1-p) = {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^{r}
になりますね。
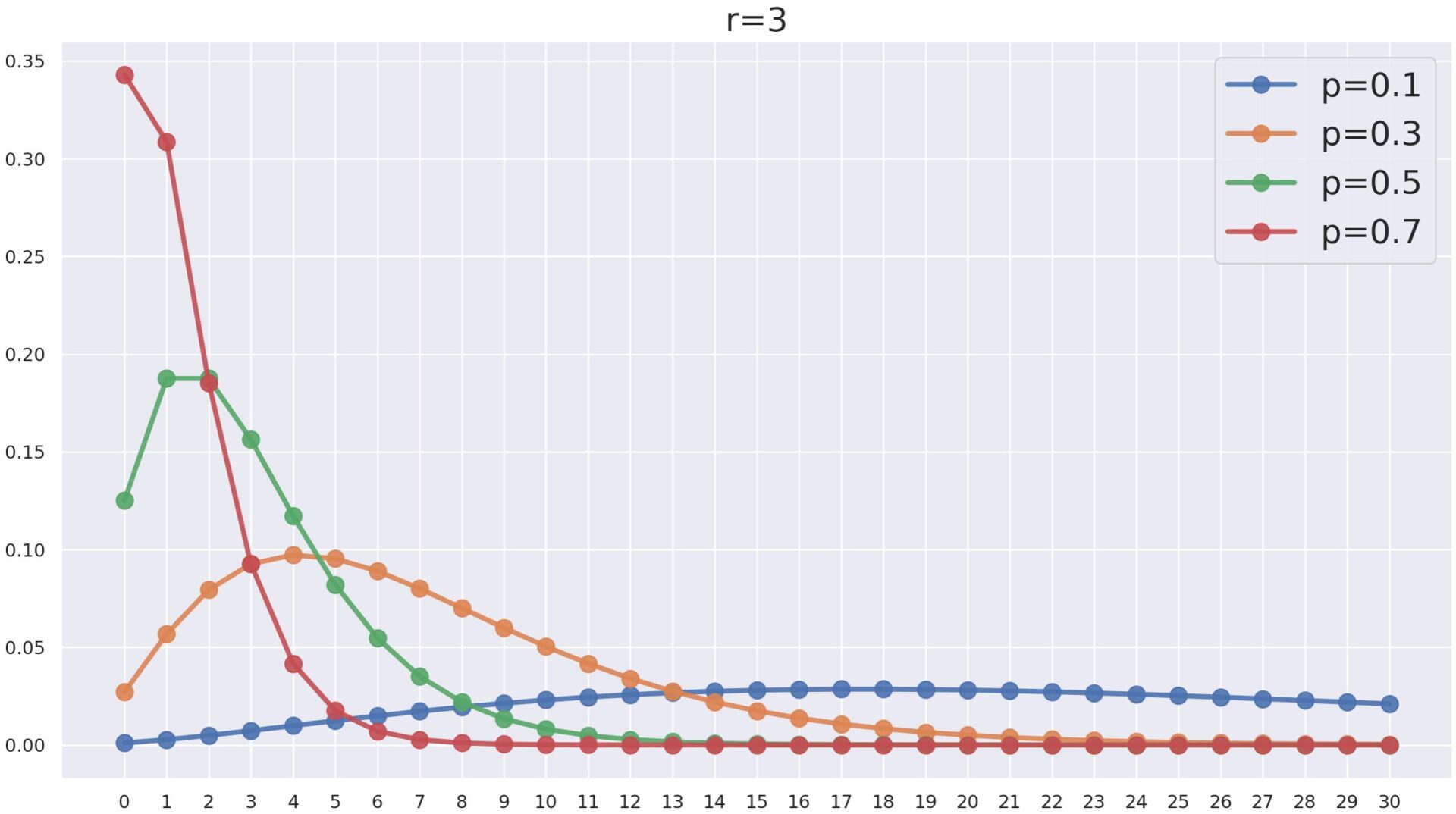
負の二項分布の確率関数のグラフ P(X=k) について， r= 3 とし， p を変化させたときの NB(3, p) は以下のようになります。
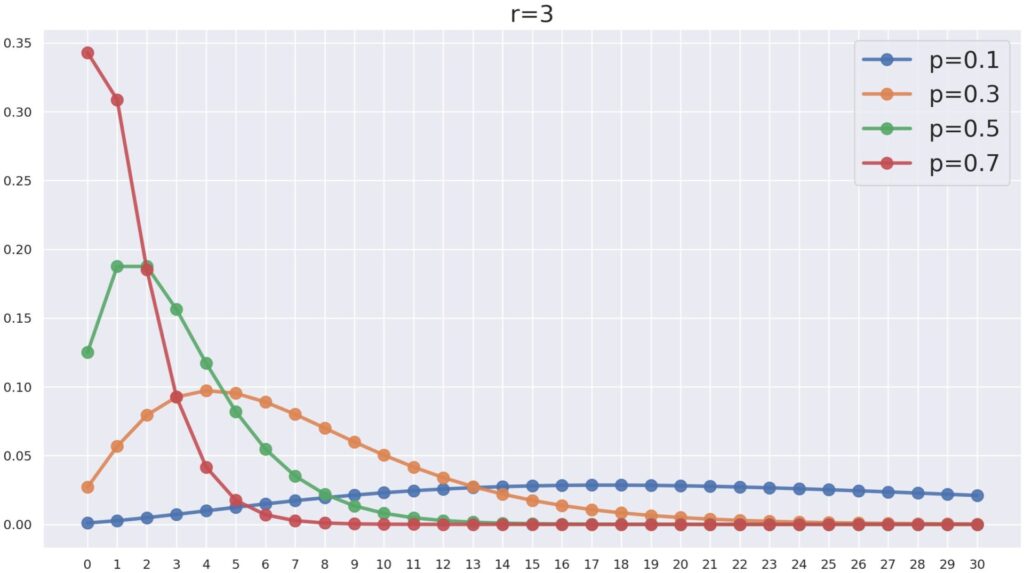
p が大きくなればなるほど，確率が k が大きな方に寄っていますね。 p が大きいと，失敗し辛くなりますから，同じ回数の失敗を重ねるまでの成功回数は増えるというわけですね。
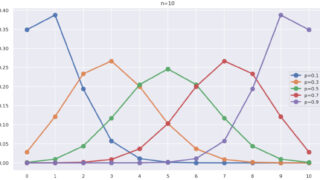
また，p=0.5 を固定し， r を変えたときの NB(r, 0.5) は以下のようになります。
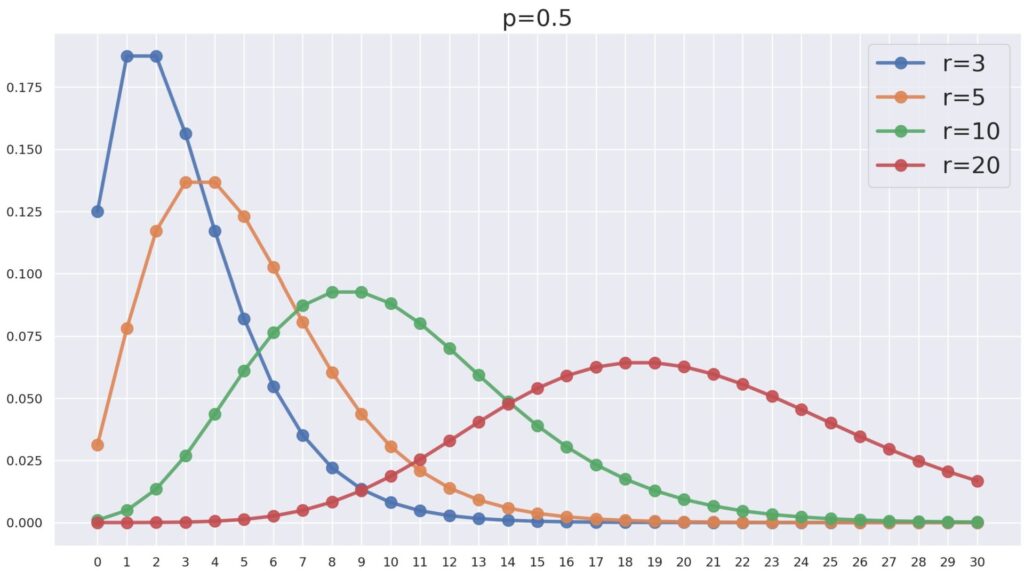
r が増えれば増えるほど，山が右に寄っていますね。これはある意味当たり前でしょう。
二項分布との違い
二項分布 B(n, p) との違いを抑えておきましょう。負の二項分布は，確率 p で表が出るコインについて， r 回ウラが出るまでの表が出る回数を表したもの であったのに対し，二項分布は，確率 p で表が出るコインを n 回投げたとき，表が出る回数を表したものでした。 コイン投げと思ったときの，両者の違いは，以下の通りです。
| コイン投げ | 二項分布 B(n,p) | 負の二項分布 NB(r, p) |
|---|---|---|
| 確率 | {}_n \mathrm{C}_k\, p^k (1-p)^{n-k} | {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r |
| 表が出る確率 | p (固定) | p (固定) |
| 試行回数の合計 | n (固定) | k+r |
| 失敗回数の合計 | n-k | r (固定) |
| 成功回数の合計 | k=0,1,2,\ldots, n | k=0,1,2,\ldots |
試行回数を固定しているのが，二項分布であり，失敗回数を固定しているのが，負の二項分布なわけですね。
二項分布については，以下の記事を参照してください。
負の二項分布の性質まとめ
負の二項分布の性質をまとめます。
| 負の二項分布 NB(r,p) | |
|---|---|
| 確率 P(X=k) | {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r |
| 確率の型 | 離散型 |
| 幾何分布との関係 | NB(1,p)+1=\operatorname{Geo}(1-p) |
| 累積分布関数 F(x) = P(X\le x) | \begin{cases} 0 & x < 0, \\ \sum_{k=0}^{\lfloor x \rfloor} {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r & x\ge 0 \end{cases} |
| 期待値 E[X] | \dfrac{pr}{1-p} |
| 分散 V(X) | \dfrac{pr}{(1-p)^2} |
| 標準偏差 \sqrt{V(X)} | \dfrac{\sqrt{pr}}{1-p} |
| 積率母関数(モーメント母関数) E[e^{tX}] | \left(\dfrac{1-p}{1-pe^t}\right)^r,\; t<-\log p |
| 特性関数 E[e^{itX}] | \left(\dfrac{1-p}{1-pe^{it}}\right)^r,\; t\in\mathbb{R} |
順番に考えていきましょう。
負の二項分布と幾何分布との関係
Y\sim \operatorname{Geo}(1-p) は，確率変数 Y がパラメータ 1-p の幾何分布に従うことを指します。
定理（負の二項分布と幾何分布との関係）
X\sim NB(1, p), \; Y\sim \operatorname{Geo}(1-p) を独立とする。このとき，
\color{red} X +1 \stackrel{\mathrm{d}}{=} Y
が成立する。ただし， \stackrel{\mathrm{d}}{=} は分布の意味で等しいことを表す。
確率 p で表が出るコイン投げで考えましょう。負の二項分布で， r=1 としたものは，1 回ウラが出るまでに表が出る回数ですね。一方で，幾何分布 \operatorname{Geo}(1-p) は， 1 回ウラが出るまでにサイコロを振る回数に相当しますから，ちょうど，上のような関係式が成立しているといえます。また，
\begin{aligned}&P(X=k) = {}_{k}\mathrm{C}_k\, p^k(1-p)\\ & = p^k(1-p) = P(Y=k+1)\end{aligned}
であることからも，分かりますね。
負の二項分布の累積分布関数(分布関数)
負の二項分布の累積分布関数(分布関数)は，
\begin{aligned}F(x) &= P(X\le x) \\ &=\begin{cases}0 & x<0 \\ \sum_{k=0}^{\lfloor x \rfloor} P(X=k) & x\ge 0 \end{cases} \\ &= \begin{cases} 0 & x < 0, \\ \sum_{k=0}^{\lfloor x \rfloor} {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r & x\ge 0 \end{cases}\end{aligned}
となります。
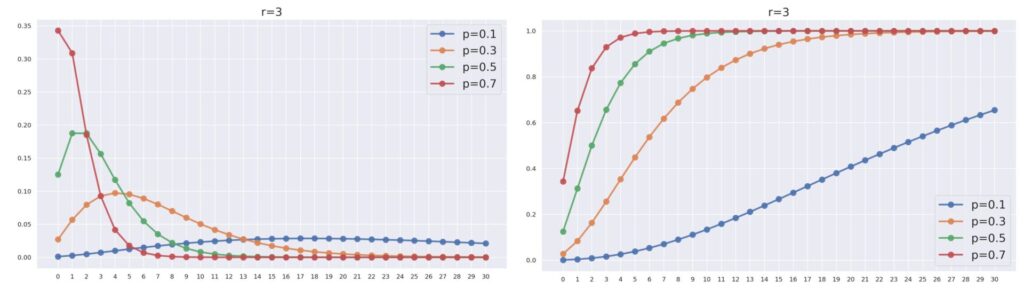
r= 3 とし， p を変化させたときの NB(3, p) とその累積分布関数の関係は，以下のようになります。
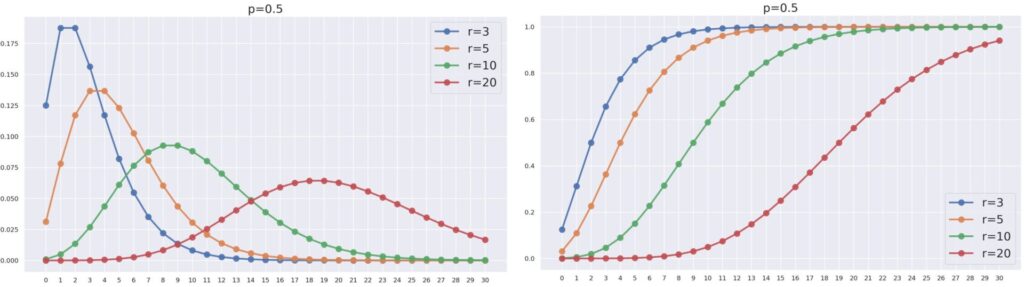
また，p=0.5 を固定し， r を変えたときの NB(r, 0.5) とその累積分布関数の関係は，以下のようになります。
負の二項分布の期待値(平均)・分散・標準偏差
定理（負の二項分布の期待値(平均)・分散・標準偏差）
X\sim NB(r, p) とする。このとき， X の期待値(平均)・分散・標準偏差は
\color{red} \begin{aligned} E[X] &= \dfrac{pr}{1-p},\\ V(X)&= \dfrac{pr}{(1-p)^2},\\ \sqrt{V(X)}&= \dfrac{\sqrt{pr}}{1-p} \end{aligned}
である。
これについては，以下の記事で解説しています。
負の二項分布の積率母関数(モーメント母関数)・特性関数
定理（負の二項分布の積率母関数(モーメント母関数)・特性関数）
X\sim NB(r, p) とする。このとき， X の積率母関数(モーメント母関数)・特性関数は
\color{red} \begin{aligned} E[e^{tX}] &= \left(\dfrac{1-p}{1-pe^t}\right)^r,\quad t<-\log p,\\ E[e^{itX}]&=\left(\dfrac{1-p}{1-pe^{it}}\right)^r,\quad t\in\mathbb{R} \end{aligned}
である。
これについては，以下で解説しましょう。
