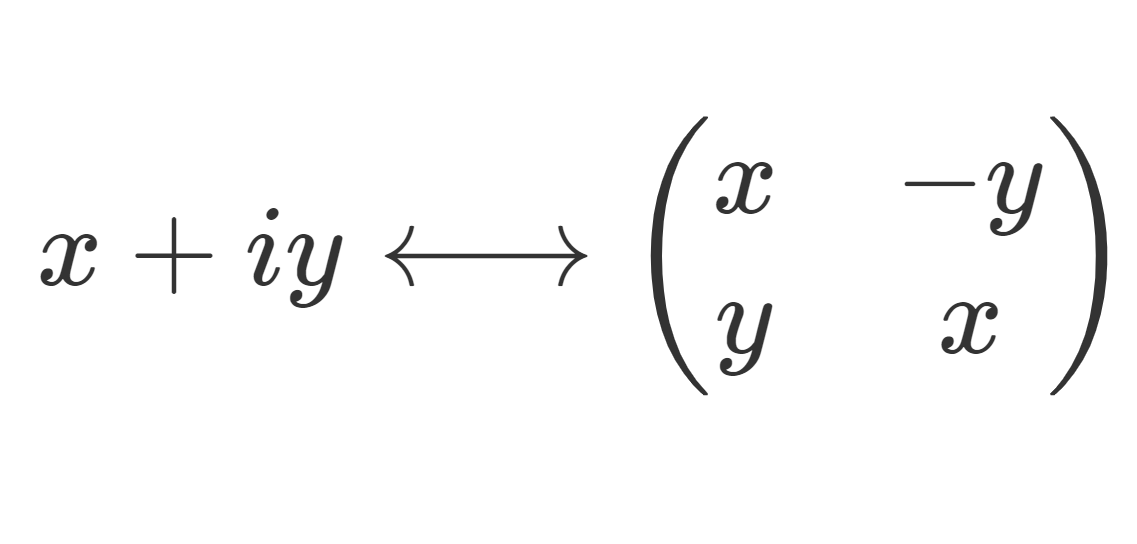複素数 x+iy の演算は,行列 \begin{pmatrix} x & -y \\ y & x \end{pmatrix} における演算と対応しています。
この対応関係について,掘り下げて考えていきましょう。
複素数と行列の対応関係
複素数 \color{red} x+iy と行列 \color{red} \begin{pmatrix} x & -y \\ y & x \end{pmatrix} は四則演算に関して対応している。
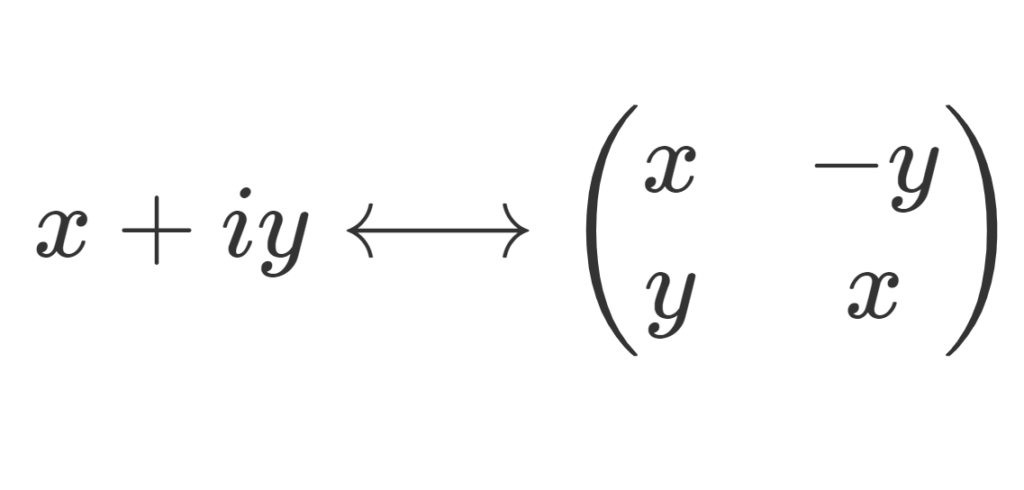
「対応」とは,ちょっとあいまいな言葉ですが,ラフにいうと「複素数の世界の四則演算」と「行列の世界の四則演算」が「同じようなものになっている」という意味です。たとえば,
ですが,この左辺・右辺それぞれの和を考えると, 1+i, \; \begin{pmatrix} 1 & -1 \\ 1& 1 \end{pmatrix} となります。これはちゃんと
になっていますね。また, i \longleftrightarrow \begin{pmatrix}0 & -1 \\ 1 & 0\end{pmatrix} それぞれの積を考えると, i^2 = -1, \; \begin{pmatrix}0 & -1 \\ 1 & 0\end{pmatrix}^2 = \begin{pmatrix}-1 & 0 \\ 0 & -1\end{pmatrix} となりますが,これについても,
となっていますね。
要するに,四則演算が対応しているとは,
\color{red}\begin{aligned}&z_1\longleftrightarrow A_1,\; z_2\longleftrightarrow A_2 \\ &\implies z_1\pm z_2 \longleftrightarrow A_1\pm A_2, \;z_1z_2 \longleftrightarrow A_1A_2\end{aligned}
などが成立することを言います。実際は,上は和・差・積だけで,商については,
と考えます。左側は単に z_1/z_2 の意味で,右辺は逆行列を考えています。
複素数と行列が対応していることの証明
さて,「対応している」ことを厳密に証明しておきましょう。
愚直に計算してもいいですが, I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} と J= \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} を用いると非常に見通しがよくなります。これを用いましょう。
証明
I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix},\; J= \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} とおくと,
\begin{pmatrix} x & -y \\ y & x \end{pmatrix} = xI+yJ
であり,また I^2 = I,\; J^2 = -I,\; IJ=JI = J もわかる。
和・差の対応関係について, a,b,c,d\in \mathbb{R} とすると,複素数の計算では
(a+bi)\pm(c+di) = (a\pm c)+(b\pm d)i
である。一方,行列の計算は
となって,対応している。
積の対応関係について, a,b,c,d\in \mathbb{R} とすると,複素数の計算では
(a+bi)(c+di) = (ac-bd)+(ad+bc)i
である。一方,行列の計算は
となって,対応している。
商の対応関係について,対応する z, A に対し, z^{-1}, A^{-1} が対応していることを示せばよい。これが示せれば,積の対応関係も用いることで,任意の2つの商の対応関係が示せたことになるからである。
a,b\in \mathbb{R}\setminus\{(0,0)\} とすると,複素数の計算では
(a+bi)^{-1} = \frac{a}{a^2+b^2} - \frac{b}{a^2+b^2}i
であり,行列の計算では,
であるから,対応している。
証明終
I が 1 , J が i に対応していて,同じような計算ができるってことですね。
「対応」のちゃんとした主張
今まで「対応」という曖昧な言葉を使ってきましたが,ちゃんと数学的に厳密な主張を述べ,終わりにしたいと思います。
定理(複素数と行列の対応関係)
複素数体 \mathbb{C} と実2次正方行列の部分体 \mathscr{C} = \left\{ \begin{pmatrix} x & -y \\ y & x\end{pmatrix} \middle| x,y\in\mathbb{R}\right\} を定める。
このとき, f\colon \mathbb{C} \to\mathscr{C} を
と定めると,これは体に関する同型写像である。
「体」とは,四則演算が定義される集合のことです。
\mathbb{C} と \mathscr{C} は,四則演算が定義された「体」としてみると,同一視できる,という意味になります。
f\colon \mathbb{C} \to\mathscr{C} が体同型とは,全単射であり,かつ四則演算を保存する,すなわち
\begin{aligned} f(z_1\pm z_2) &= f(z_1)\pm f(z_2), \\ f(z_1z_2) &= f(z_1)f(z_2),\\ f(z^{-1}) &= f(z)^{-1}\end{aligned}
が成立することを指します。四則演算の対応については,上で確認しましたね。