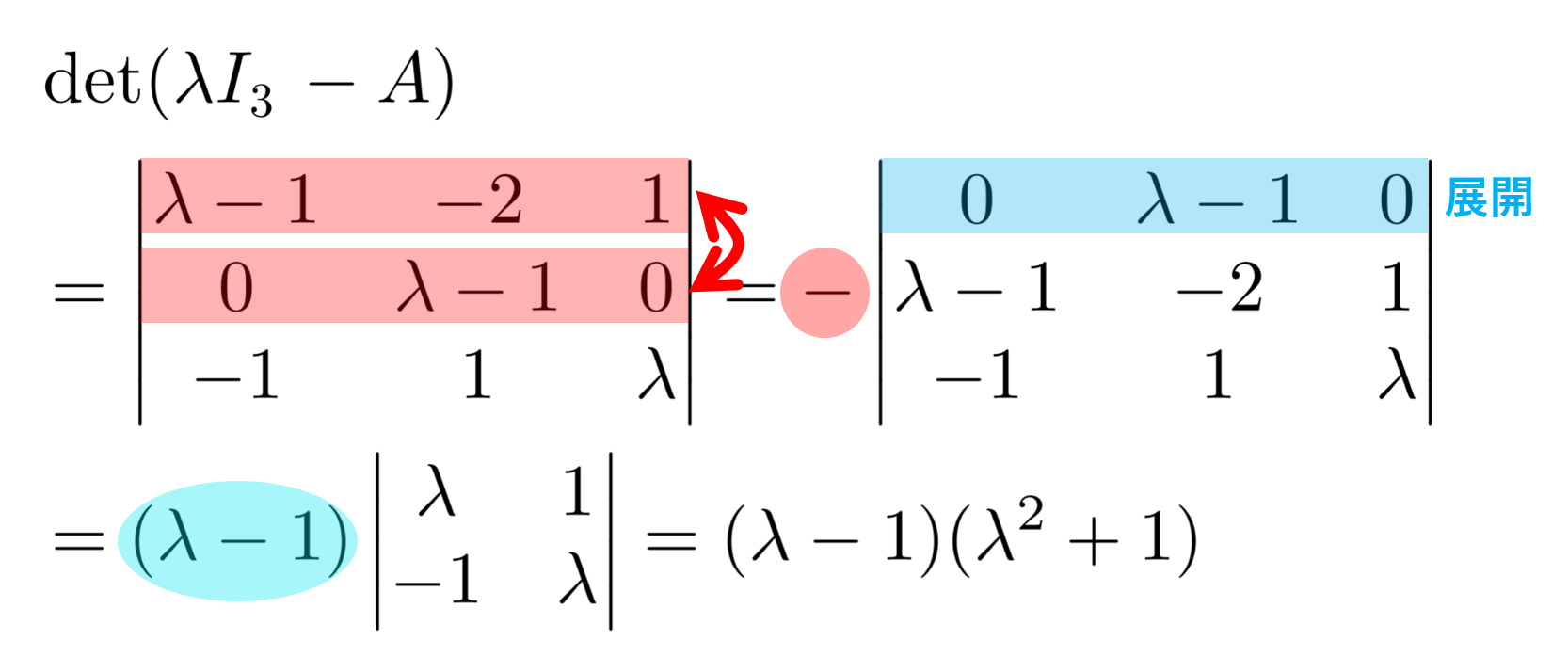
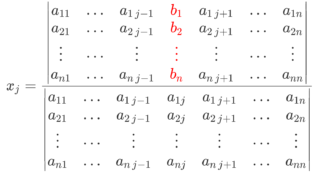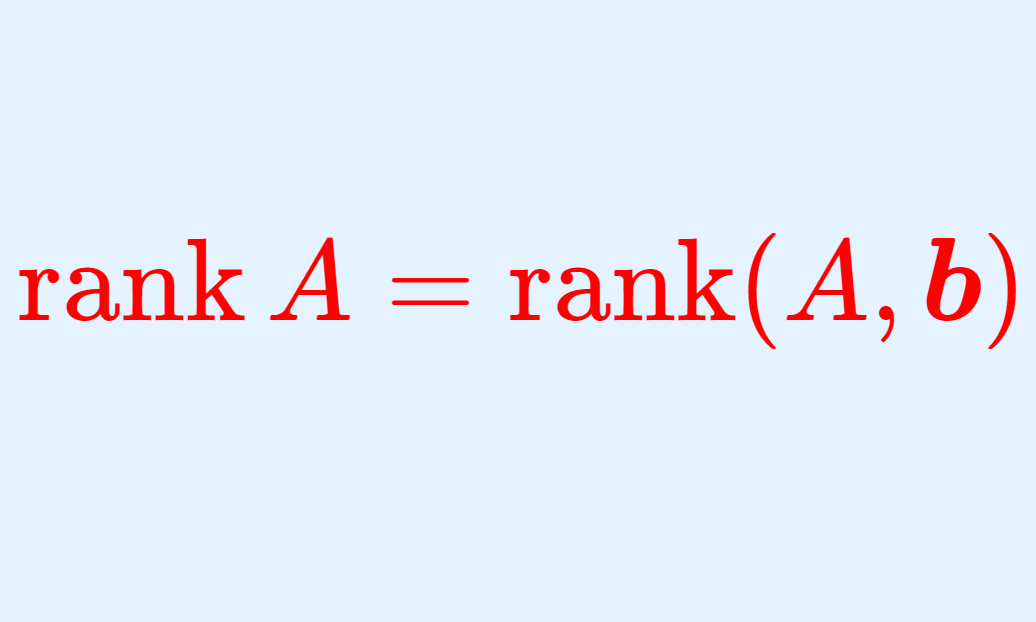連立方程式 \begin{cases} 2x -3y = 1 \\ x-y=0\end{cases} を行列で表すと,
\begin{pmatrix}2 & -3 \\ 1 & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}
と表せます。このときの \begin{pmatrix}2 & -3 \\ 1 & -1 \end{pmatrix} を「係数行列」といい,これと右辺を合体させた \begin{pmatrix}2 & -3 & 1\\ 1 & -1 & 0 \end{pmatrix} を「拡大係数行列」といいます。
これについて,一般的な定義と具体例を紹介します。
係数行列・拡大係数行列の定義
定義(係数行列・拡大係数行列)
連立一次方程式
\begin{cases} a_{11}x_1+a_{12}x_2+\cdots + a_{1n}x_n = b_1 \\ a_{21}x_1+a_{22}x_2+\cdots + a_{2n}x_n = b_2 \\ \ldots \\ a_{m1}x_1+a_{m2}x_2+\cdots + a_{mn}x_n = b_m \end{cases}
は,行列を用いて表すと
とかける(m\ne n でも良いことに注意)。この式に対応して, A\boldsymbol{x} = \boldsymbol{b} とかくことにしよう。このときの m\times n 行列
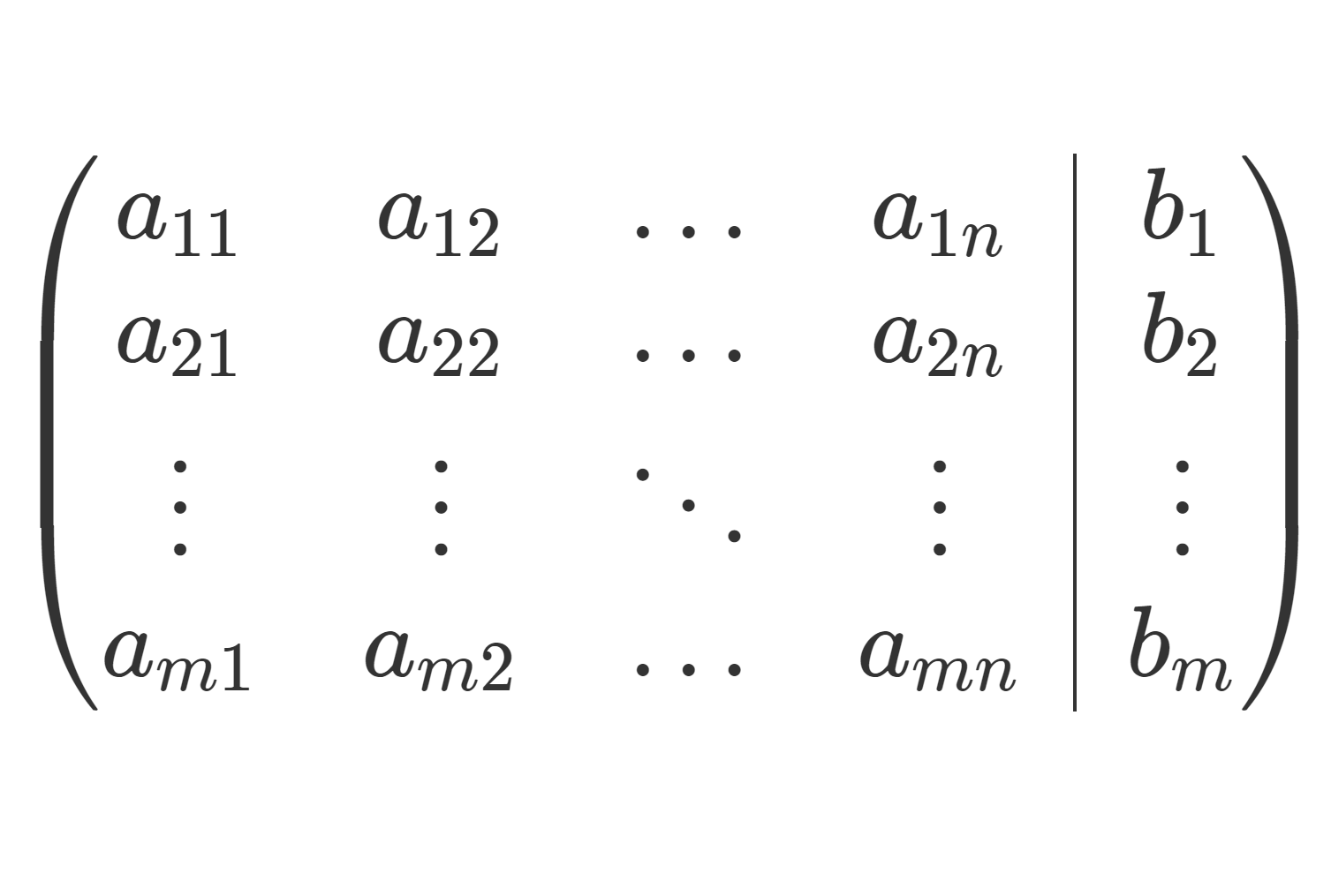
を係数行列 (coefficient matrix) という。また,A と \boldsymbol{b} を並べた m\times (n+1) 行列
を拡大係数行列 (augmented coefficient matrix) という。
拡大係数行列は, A と \boldsymbol{b} をつなげたものですが,その境目を明確にするため,縦棒 | を入れて
\left(\!\!\!\begin{array}{c|c} A&\boldsymbol{b}\end{array}\!\!\!\right) = \left(\!\!\!\begin{array}{cccc|c} a_{11} & a_{12} &\dots & a_{1n} & b_1 \\ a_{21} & a_{22} &\dots & a_{2n} &b_2\\ \vdots & \vdots &\ddots & \vdots &\vdots\\ a_{m1} & a_{m2}& \dots & a_{mn} &b_m \end{array}\!\!\!\right)
と表すこともあります。
係数行列・拡大係数行列の具体例
一つだけ具体例を挙げましょう。
例1.
連立一次方程式 \begin{cases} 2x_1 + 3x_2 - 5x_3 = 2 \\ -x_1 + 2x_3 = 1 \end{cases} を行列を用いて表すと,
\begin{pmatrix} 2 & 3 & -5 \\ -1 & 0 & 2 \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \\ x_3\end{pmatrix} =\begin{pmatrix} 2 \\1 \end{pmatrix}
とかけるため,係数行列は
であり,拡大係数行列は
である。