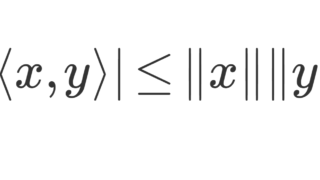数学における勾配 (gradient) とは,各偏微分を並べたもので, \operatorname{grad} f= \left( \frac{\partial f}{\partial x_1}, \dots, \frac{\partial f}{\partial x_n} \right) を指します。
勾配の具体的な定義と,そのベクトルが表す意味について,解説しましょう。
勾配(grad)の定義
以下では, D\subset\mathbb{R}^n を n 次元領域とし, f\colon D\to \mathbb{R} としましょう。
定義(勾配)
n 変数関数 f(x_1,x_2,\dots,x_n) が偏微分可能であるとき
\color{red} \operatorname{grad} f= \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \dots, \frac{\partial f}{\partial x_n} \right)
を f の勾配 (gradient) という。勾配は \color{red}\operatorname{grad}f の他, \color{red} \nabla f, \vec{\nabla} f などと書かれる。
\nabla はナブラ (nabla) と呼ばれる記号です。
各偏微分を並べたものを,勾配というのですね。一変数のときは,微分は一つでしたが,多変数だとそうはいきません。ある意味,「勾配とは多変数関数の微分(のかたまり)」と言えます。勾配はベクトルのため,勾配ベクトルとも言います。
たとえば, f(x,y)=x^2 + y^3 について, \operatorname{grad} f= (f_x, f_y) = (2x, 3y^2) となります。
勾配(grad)の意味
勾配の意味を,方向微分との関連性の観点から,2つ述べましょう。
勾配と各方向微分の関係は内積で表せる
定理1(勾配と方向微分)
f を全微分可能とする(たとえば, f_x,f_y が存在して連続であればよい)。このとき,\boldsymbol{v} = (v_1,v_2,\dots, v_n) 方向の方向微分 \nabla_{\boldsymbol{v}} f は
\color{red} \begin{aligned}\nabla_{\boldsymbol{v}} f &= \langle \operatorname{grad} f, \boldsymbol{v}\rangle \\ &= v_1\frac{\partial f}{\partial x_1}+ v_2\frac{\partial f}{\partial x_2} +\dots + v_n\frac{\partial f}{\partial x_n} \end{aligned}
とかける。ただし, \langle \cdot, \cdot \rangle は内積を指す。
方向微分は \displaystyle \nabla_{\boldsymbol{v}} f (\boldsymbol{x}) = \lim_{h\to 0}\dfrac{ f(\boldsymbol{x}+h\boldsymbol{v})-f(\boldsymbol{x})}{h} と定義されます。これが, \operatorname{grad}f と \boldsymbol{v} の内積でかけると言っているんですね(→方向微分とは~定義・性質・求め方を詳しく~)。
復習ですが,「全微分可能」とは,1次近似可能であること,ラフに言うと接平面が考えられることを意味します(→全微分の定義・性質・求め方を詳しく解説~全微分可能性~)。
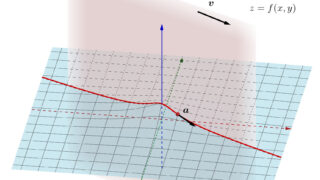
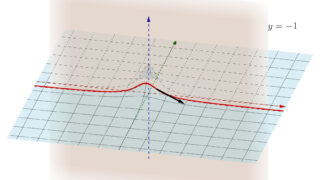
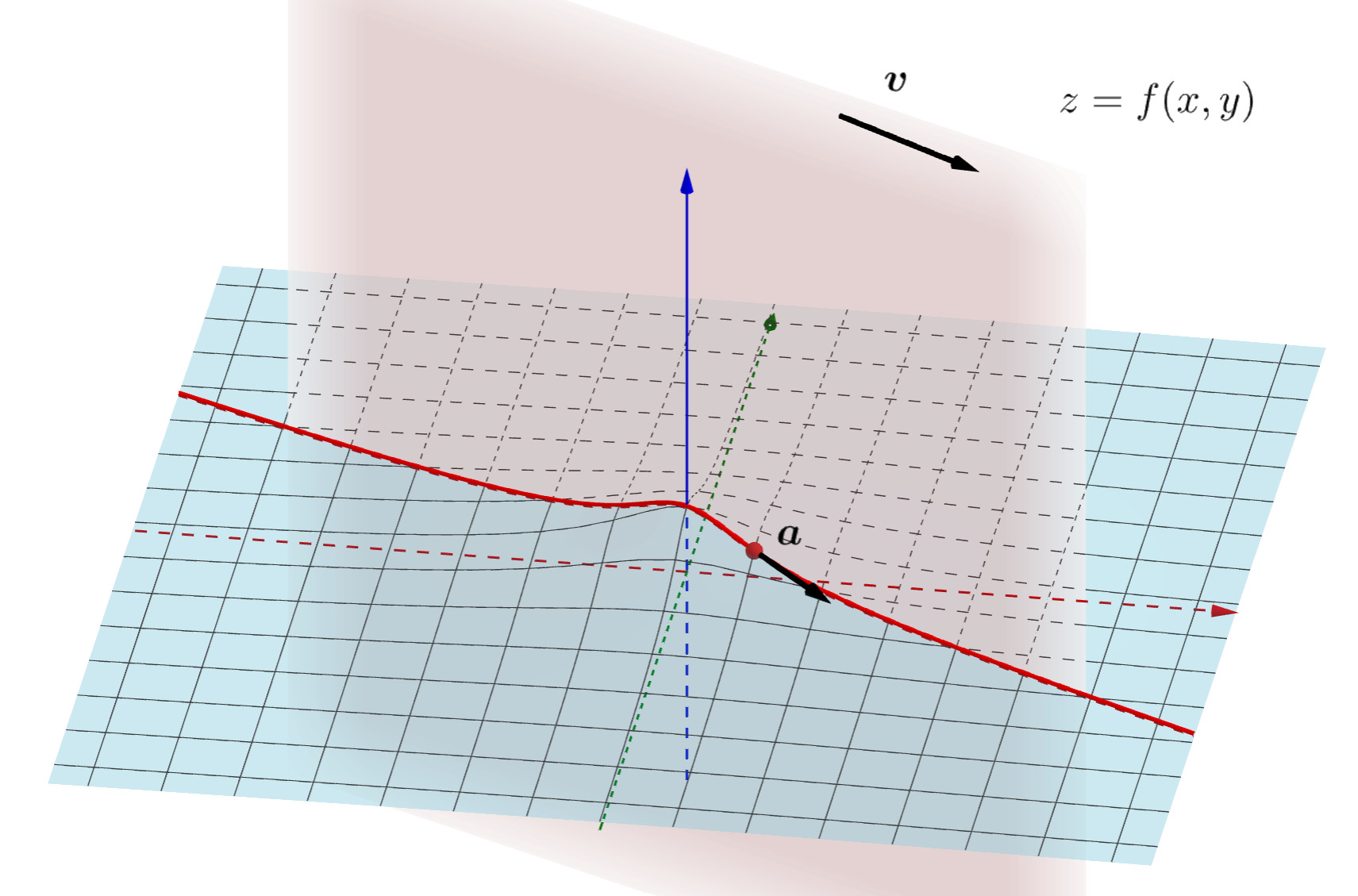
n=2 の場合を考えましょう。全微分可能ですから,接平面を考えることが可能です。よって,求める方向微分は, \boldsymbol{v} が単位ベクトルのとき,接平面におけるその方向の傾きに等しくなります。以下のようなイメージです。
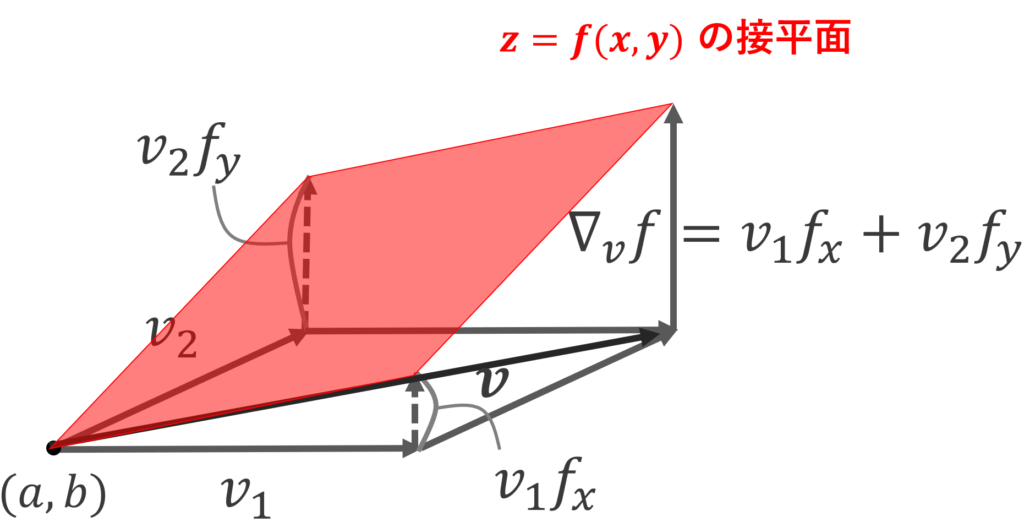
方向微分の詳細や,この証明は,以下の記事で行っています。
勾配は,最も傾斜が大きくなる向きとその大きさである
次の定理はしっかりと覚えておきたいところです。
定理2(勾配と最大傾斜)
f を全微分可能とする(たとえば, f_x,f_y が存在して連続であればよい)。 方向微分 \displaystyle \nabla_{\boldsymbol{v}} f (\boldsymbol{x}) = \lim_{h\to 0}\dfrac{ f(\boldsymbol{x}+h\boldsymbol{v})-f(\boldsymbol{x})}{h} が最大となるような単位ベクトル \boldsymbol{v} は
\color{red} \boldsymbol{v}=\frac{\operatorname{grad}f}{\| \operatorname{grad}f\|}
であり,そのときの方向微分係数は \color{red} {\| \operatorname{grad}f \|} である。
ここで, \boldsymbol{v}=(v_1,v_2,\dots, v_n) に対し, \|\boldsymbol{v}\| = \sqrt{v_1^2+v_2^2+\dots +v_n^2} はベクトルの大きさ(ノルム)を指します。
勾配の方向は最大傾斜の方向であり,その大きさは勾配の大きさであるということですね。
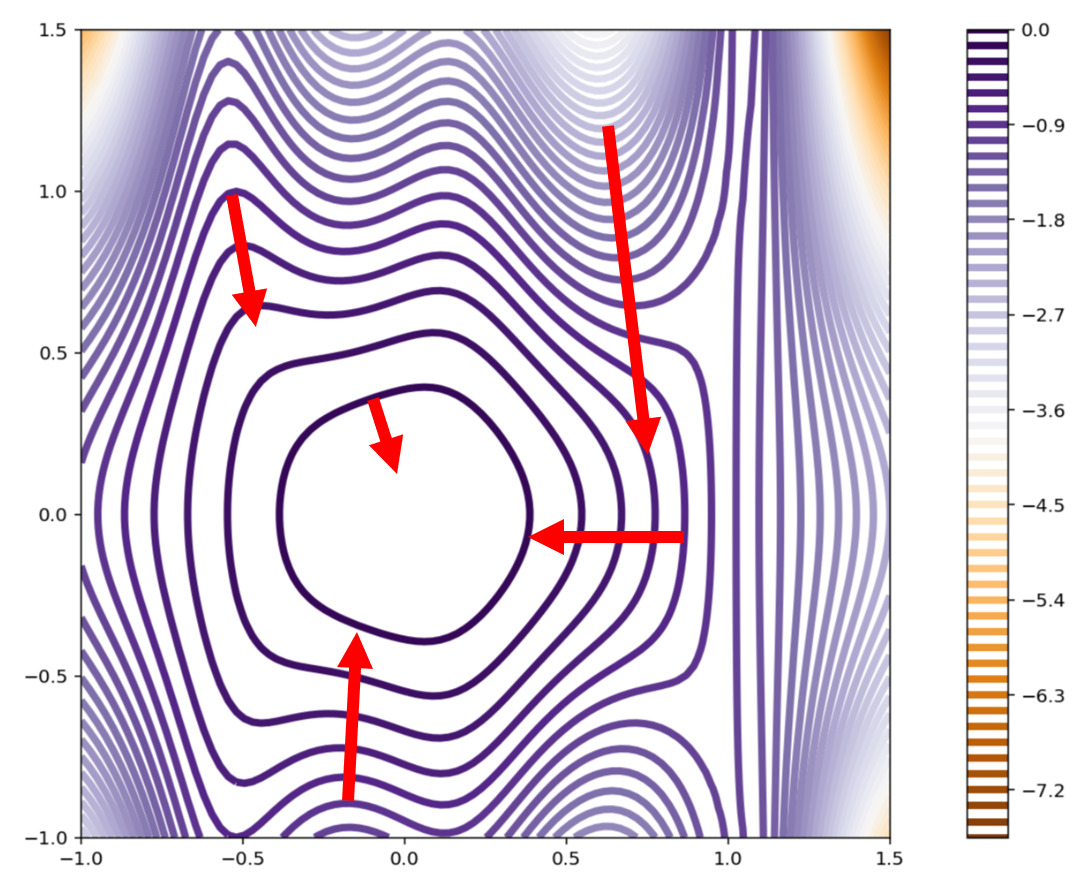
以下は,全微分可能な関数 f(x,y) の値を, xy 平面上に等高線で図示し,何点か \operatorname{grad}f の方向を赤矢印で表現したものです。 \operatorname{grad} f の向きは最大傾斜方向ですから,等高線と垂直になり,また矢印の大きさは傾斜の大きさですから,等高線が密なところの矢印の方が大きくなります。
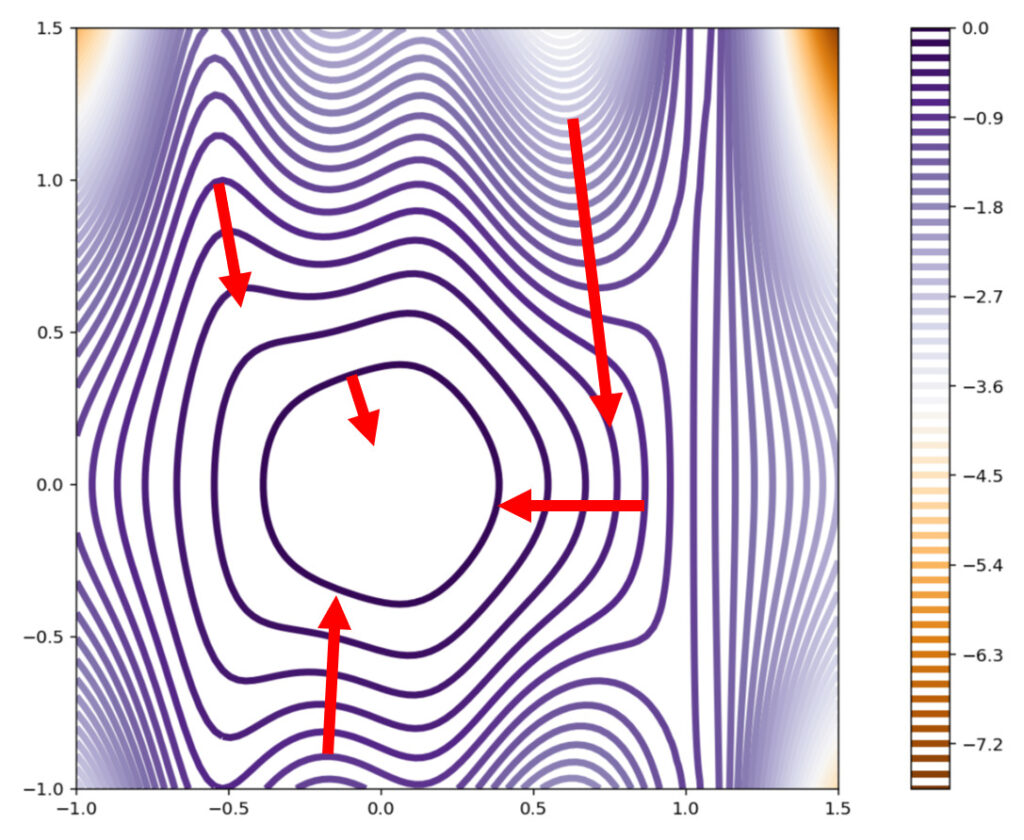
証明は,コーシーシュワルツの不等式を用いれば簡単です。
証明
\boldsymbol{v} を単位ベクトルとする。定理1より, \nabla_{\boldsymbol{v}} f = \langle \operatorname{grad} f, \boldsymbol{v}\rangle (右辺は内積)である。コーシーシュワルツの不等式より,
\|\operatorname{grad} f\| \le \langle \operatorname{grad} f, \boldsymbol{v}\rangle \le \|\operatorname{grad} f\|
である。左辺・右辺の等号成立はそれぞれ \boldsymbol{v}=-\dfrac{\operatorname{grad}f}{\| \operatorname{grad}f\|}, \dfrac{\operatorname{grad}f}{\| \operatorname{grad}f\|} のときである。
証明終
なお,このことから,一般に \boldsymbol{v} が単位ベクトルのとき,
- \|\operatorname{grad}f\|\le \nabla_{\boldsymbol{v}} f \le \|\operatorname{grad}f\|
であり,等号成立は \boldsymbol{v}=\pm\dfrac{\operatorname{grad}f}{\| \operatorname{grad}f\|} のときです。