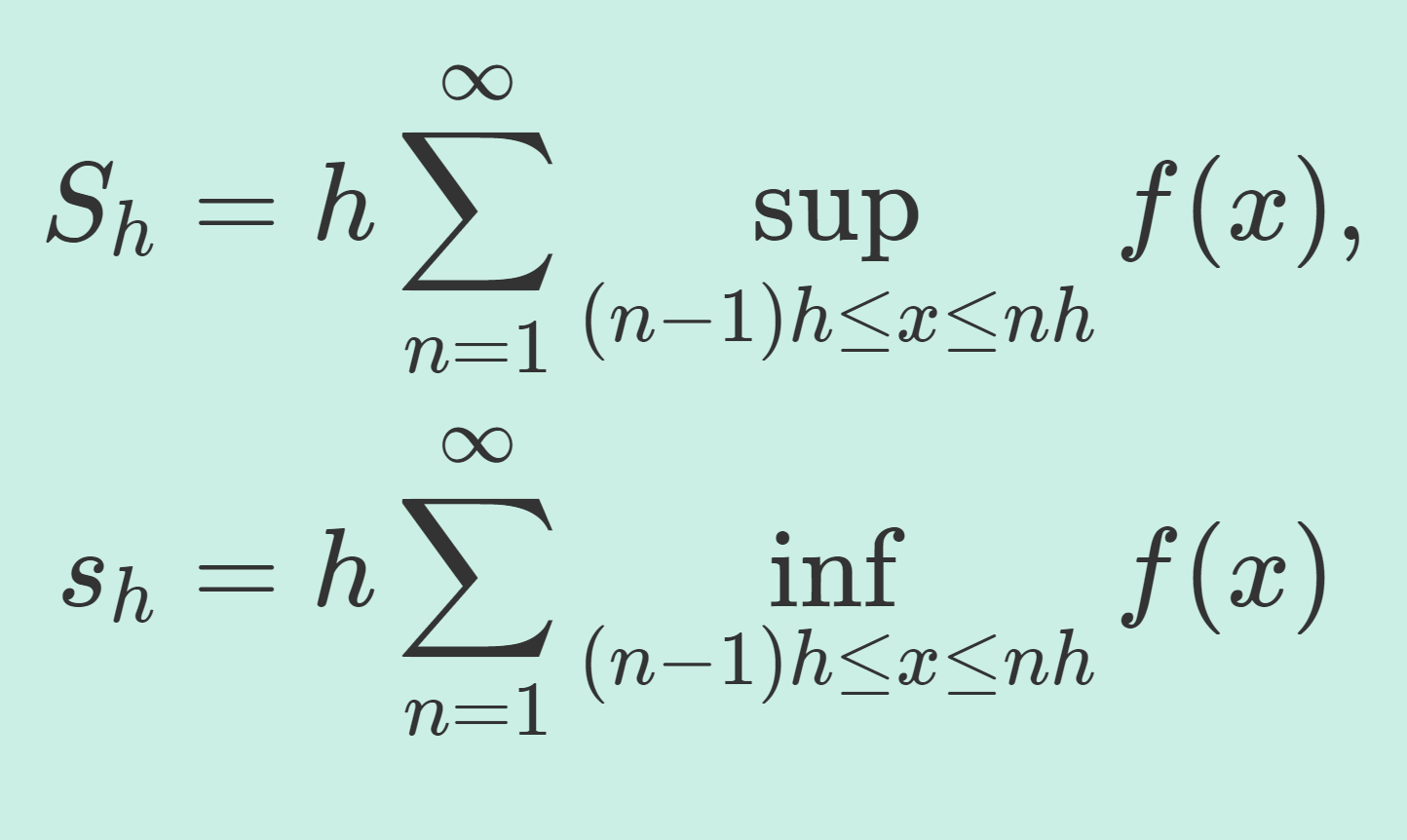重積分とは～定義と面積確定集合～

大学数学で初めて出てくる積分である「重積分」について，その定義と，面積確定集合とは何かについて，図解付きで解説します。

2重積分の定義と面積確定集合
1. 2重積分の定義
2. 面積確定集合
n重積分の定義
多重積分の性質
関連する記事

2重積分の定義と面積確定集合

まずは， $2$ 変数の場合を考えてみましょう。

2重積分の定義

定義の仕方は，一変数のリーマン積分と類似しています。一変数のリーマン積分の定義が分からない場合は，まずはリーマン和による定積分の定義とリーマン積分可能・不可能な例を参照した方が良いかもしれません。

定義（ $2$ 重積分）

$I_1 = [a,b],\; I_2=[c,d],\; D=I_1\times I_2$ とし， $f\colon D\to \mathbb{R}$ を有界な2変数関数とする。各区間を

\begin{gathered}a=x_0<x_1<x_2<x_3 < \dots < x_m=b,\\ c=y_0<y_1<y_2 <y_3<\dots < y_n=d \end{gathered}

かつ $D_{i,j} = [x_{i-1}, x_{i}]\times [y_{j-1}, y_{j}] \;(1\le i\le m,\, 1\le j\le n)$ とすることで， $D$ を $mn$ 個の長方形領域に分ける。

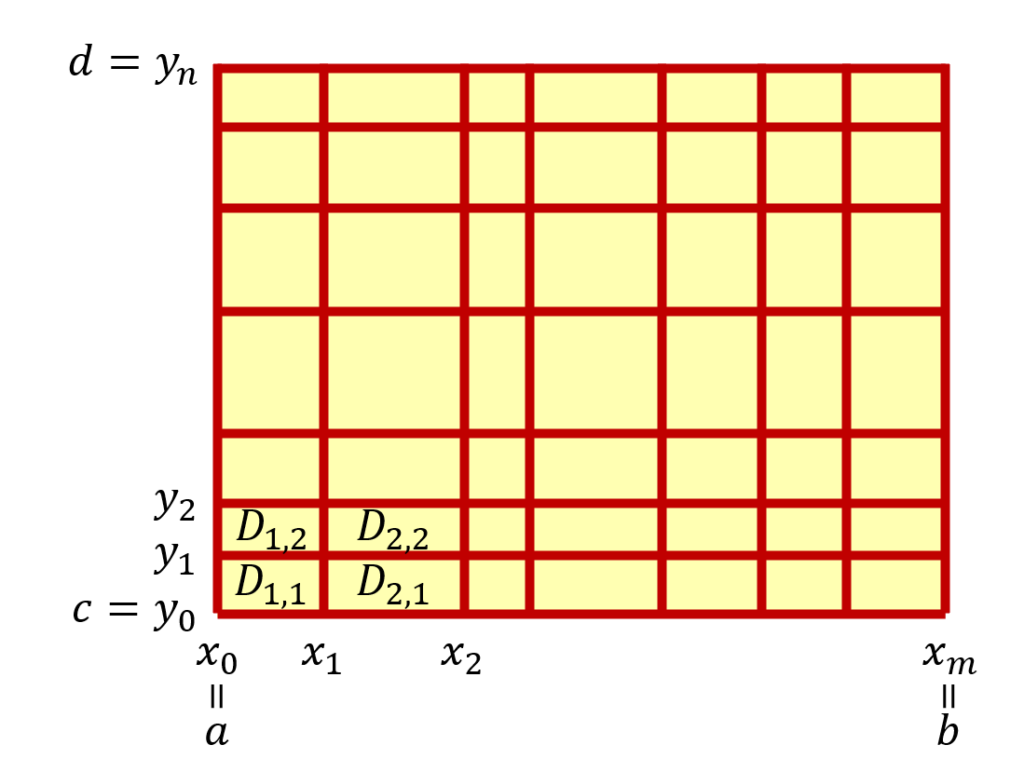
さらに $\Delta x_i = x_i-x_{i-1}\;, \Delta y_j=y_j-y_{j-1}$ とし，

\!\!\!|\Delta| = \max\{ \Delta x_i, \Delta y_j\mid 1\le i\le m,\,1\le j\le n\}

と定め，各領域から $t_{i,j}\in D_{i,j}$ を一つ選ぶ。このときのリーマン和 (Riemann sum)

\color{red}\sum_{\substack{1\le i\le m \\ 1\le j\le n}} f(t_{i,j}) \Delta x_i \Delta y_j

について，

\lim_{|\Delta |\to 0+} \sum_{\substack{1\le i\le m \\ 1\le j\le n}} f(t_{i,j}) \Delta x_i \Delta y_j

が $\{D_{i,j}\}, \{t_{i,j}\}$ に依らずに同じ値に収束するとき，その収束値を

\color{red} \iint_D f(x,y)\,dxdy

とかき，これを $f$ の $D$ 上の重積分 (multiple integral) という。

$2$ 次元領域の積分なので，便宜上 $\displaystyle \iint_D f(x,y)\, dxdy$ とかきましたが， $x\in \mathbb{R}^2$ と考え， $\color{red} \displaystyle \int_D f(x) dx$ というかき方をすることもあります。

さて，1変数の定積分(リーマン積分)の定義を理解しているのであれば，同じような定義だと気づくでしょう。

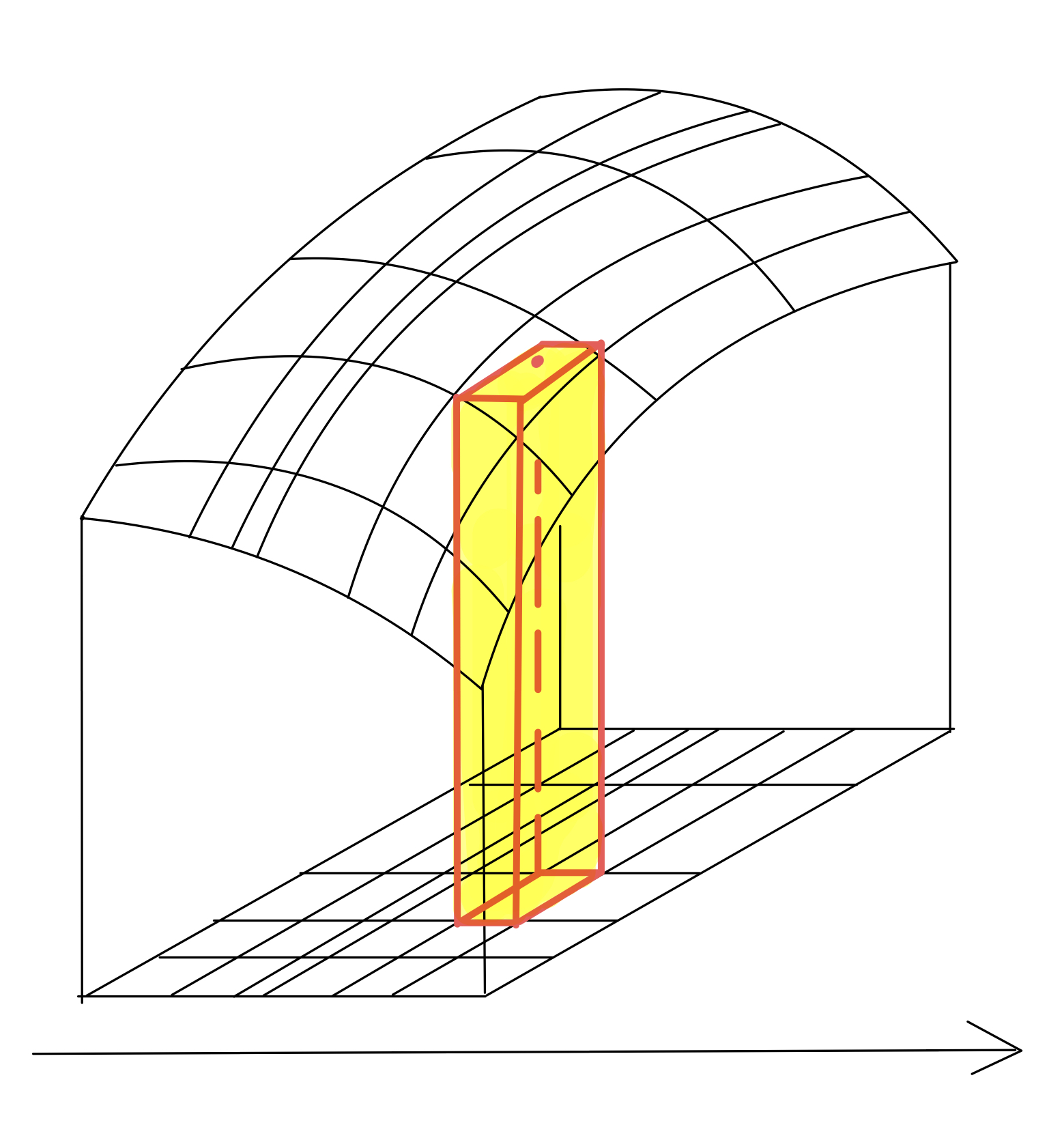
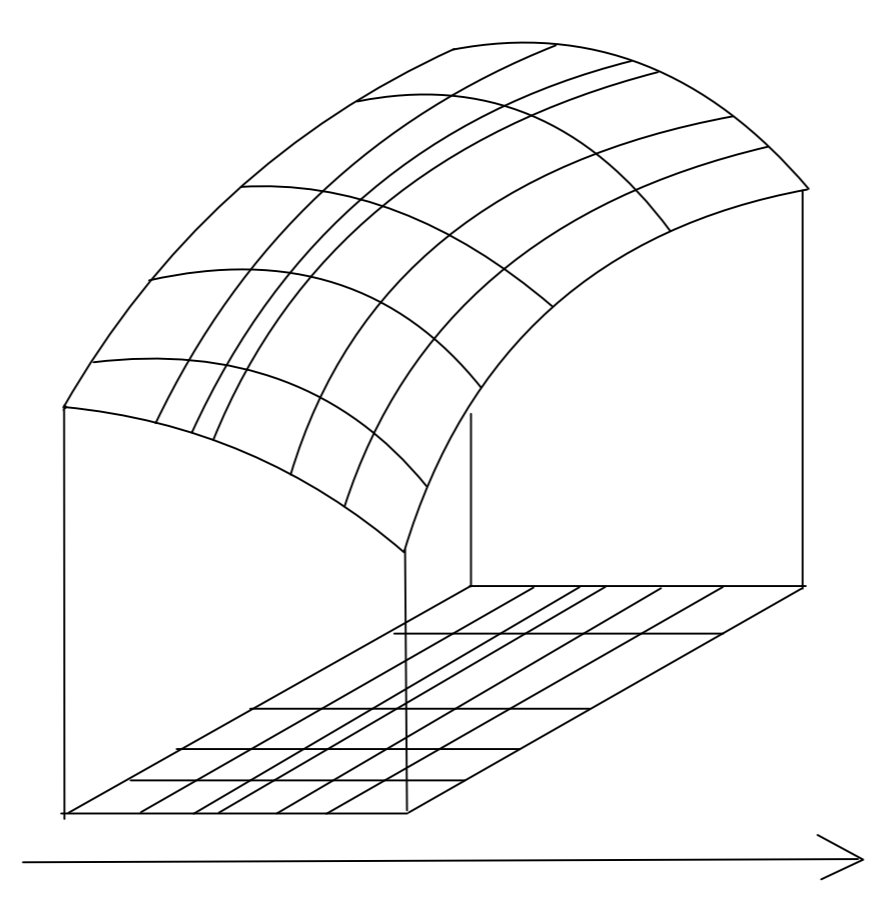
1変数のときは，長方形近似により， $y=f(x)$ と $x$ 軸の間の面積を近似していました。2変数のときは，直方体近似により， $z=f(x,y)$ と $xy$ 平面の間の体積を近似しています。以下の図がそのイメージです。

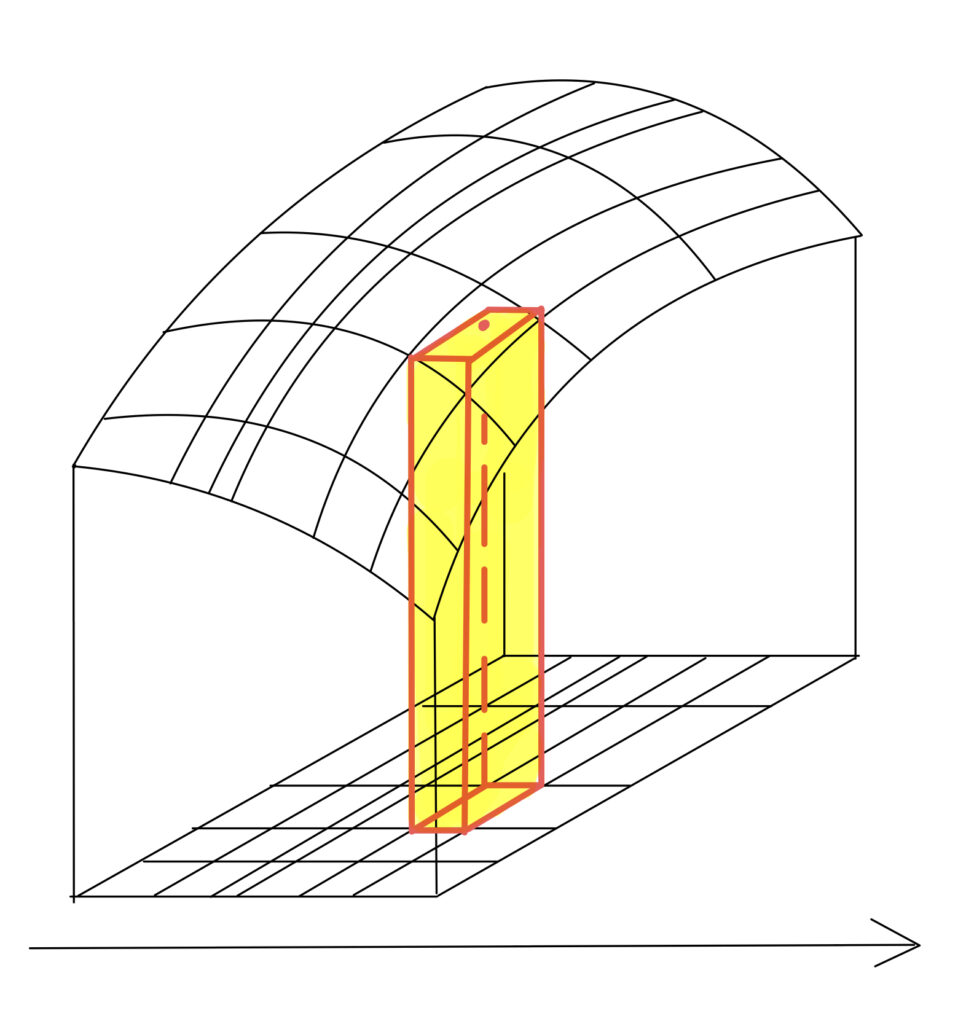
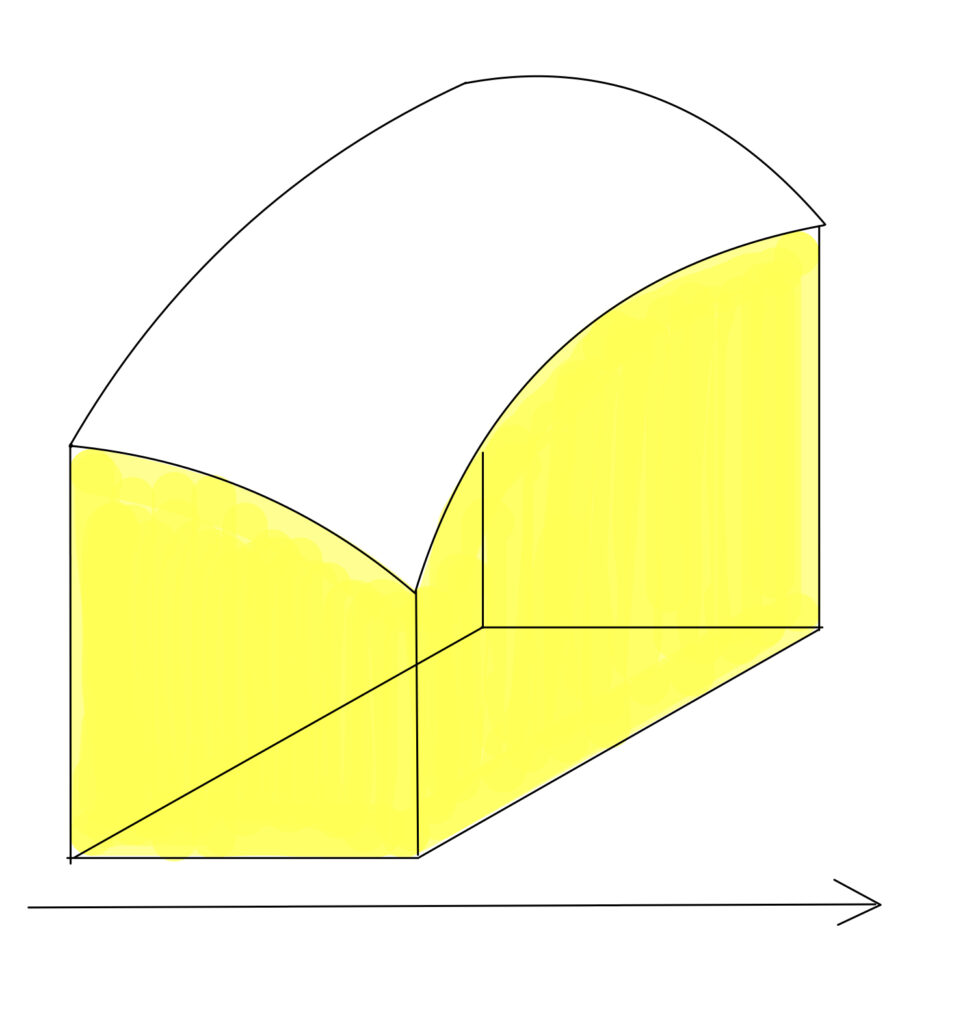
長方形領域を小さくすると，平面z=f(x,y)とxy平面で囲まれた部分の面積を表すようになる図 — 長方形領域を細かくしていくと，結局黄色い部分の面積の近似になる

なお，領域 $D$ は閉区間2つの直積で表せるものしか考えていませんが，より一般の集合 $E\subset \mathbb{R}^2$ 上の２重積分は

\color{red}\iint_E f(x,y)\, dxdy = \iint_D 1_E(x,y)f(x,y)\,dxdy

で定義すればよいです。ただし， $1_E (x,y)= \begin{cases} 1& (x,y)\in E,\\ 0 & (x,y)\in E^c\end{cases}$ を定義関数とします。

面積確定集合

続いて，面積確定集合を定義しましょう。面積確定集合は，上の2重積分をもってして定義されます。

定義（面積確定集合）

$F\subset \mathbb{R}^2$ が面積確定集合であるとは， $F\subset D=[a,b]\times [c,d]$ としたときに，定義関数 $1_F(x,y)=\begin{cases} 1& (x,y)\in F, \\ 0 & (x,y)\in D\setminus F\end{cases}$ が重積分可能であること，すなわち，

\color{red}\iint_D 1_F (x,y)\, dxdy

が定義できることを言う。また，このときの上の値を $F$ の面積 (area) という。

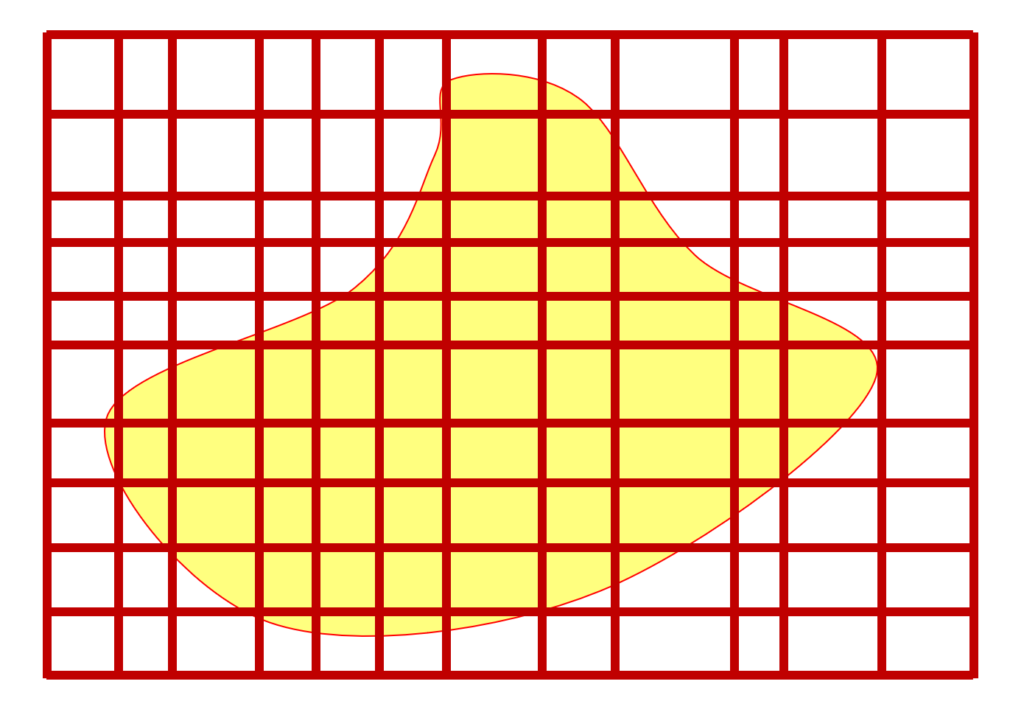
どんどん長方形を細かくしていることで，黄色い部分を近似して，面積を求めています。やっていることは，まさに面積の長方形近似ですね。

例を挙げましょう。

面積確定集合の例

$A=\{ (x,y)\in\mathbb{R}^2\mid 0\le x\le y\le 1\}$ は面積確定集合である。
$B = \{ (x,y)\in \mathbb{R}^2\mid x,y\in\mathbb{Q}\}$ は面積確定集合でない。

n重積分の定義

続いて，一般の $n$ 重積分を定義しておきましょう。

定義（ $n$ 重積分）

$I_1=[a_1, b_1], \,I_2=[a_2,b_2],\, \dots, I_n=[a_n,b_n]$ を閉区間， $D=I_1\times I_2\times \dots \times I_n$ とし， $f\colon D\to \mathbb{R}$ を有界な $n$ 変数関数とする。各区間を

\begin{gathered} a_1=x_{1,0}<x_{1,1}<x_{1,2}<\dots< x_{1,m_1}=b_1, \\ a_2=x_{2,0}<x_{2,1}<x_{2,2}<\dots< x_{2,m_2}=b_2, \\ \cdots \\ a_n=x_{n,0}<x_{n,1}<x_{n,2}<\dots< x_{n, m_n}=b_n, \\ \end{gathered}

と分割する。また，各 $d$ 次元直方体領域を $D_{i_1,i_2, \dots, i_n}= [x_{1,i_1-1}, x_{1,i_1}] \times [x_{2,i_2-1}, x_{2,i_2}] \times \dots \times [x_{n,i_n-1}, x_{n,i_n}]$ とし，さらに $\Delta x_{k, i} = x_{k,i}-x_{k,i-1}$ とおき，

|\Delta|=\max\{\Delta x_{k,i}\mid 1\le k\le n, 1\le i\le m_n\}

と定め，各領域から $t_{i_1,i_2,\dots, i_n} \in D_{i_1,i_2, \dots, i_n}$ を選ぶ。このときのリーマン和 (Riemann sum)

\color{red}\sum_{\substack{1\le i_1\le m_1\\ 1\le i_2 \le m_2\\ \dots \\ 1\le i_n\le m_n}} f(t_{i_1,i_2,\dots, i_n}) \Delta x_{i_1} \Delta x_{i_2}\dots \Delta x_{i_n}

について，

\lim_{|\Delta|\to 0+} \sum_{\substack{1\le i_1\le m_1\\ 1\le i_2 \le m_2\\ \dots \\ 1\le i_n\le m_n}} f(t_{i_1,i_2,\dots, i_n}) \Delta x_{i_1} \Delta x_{i_2}\dots \Delta x_{i_n}

が $\{D_{i_1,i_2,\dots, i_n}\}, \{t_{i_1,i_2,\dots, i_n}\}$ に依らずに同じ値に収束するとき，その収束値を

\color{red} \int\dots \int_D f(x_1,x_2,\dots, x_n)\,dx_1dx_2\dots dx_n

とかき，これを $f$ の $D$ 上の重積分 (multiple integral) という。

$\displaystyle \int\dots\int$ とかきましたが， $\displaystyle \int$ の個数は $n$ 個です。

これも $x\in \mathbb{R}^n$ として，単に $\color{red} \displaystyle \int_D f(x)\, dx$ とかくこともあります。

これは，図形的に描くのはできませんが，イメージとしては，底面が $n$ 次元である直方体を用いて， $z=f(x_1,x_2,\dots, x_n)$ と $x_1x_2\dots x_n$ 超平面の間の $n$ 次元体積を近似していると思えます。

また，積分範囲として閉区間の直積しか考えていませんが，より一般の集合 $E\subset \mathbb{R}^n$ については，

\color{red}\begin{aligned}&\int\dots\int_E f(x_1,\dots, x_n)\, dx_1\dots dx_n \\&= \int\dots\int_D 1_E(x_1,\dots,x_n)f(x_1,\dots,x_n)\,dx_1\dots dx_n\end{aligned}

と定義すればよいです。ただし， $1_E (x_1,\dots x_n)= \begin{cases} 1& (x_1,\dots, x_n)\in E,\\ 0 & (x_1,\dots,x_n)\in E^c\end{cases}$ を定義関数とします。

また，2変数の場合と同様に， $n$ 次元体積確定集合を考えることが可能です。

多重積分の性質

重積分においても，１変数と同じような性質が成立します。簡単に述べておきましょう。

ここでは，簡単のため， $x\in\mathbb{R}^n,\; D\subset\mathbb{R}^n$ として， $n$ 重積分を $\int_D f(x)\, dx$ とかく表記を用います。ここで， $n\ge 1$ ですから，以下は $n=1$ の場合（単なる1変数の積分の場合）も成立します。

定理（多重積分の性質）

D, D_1,D_2\subset \mathbb{R}^n とし， f,g\colon \mathbb{R}^n \to \mathbb{R} を D,D_1,D_2 上可積分であるとする。このとき，
1. $\alpha, \beta \in \mathbb{R}$ に対して，
  $\begin{aligned}&\int_D (\alpha f(x)+\beta g(x)) \,dx\\ &= \alpha \int_D f(x)\,dx+\beta \int_D g(x)\,dx. \end{aligned}$
2. $f$ は $D_1\cup D_2, D_1\cap D_2$ 上も可積分であり，
  $\begin{aligned} &\int_{D_1 \cup D_2} f(x)\,dx+ \int_{D_1\cap D_2} f(x)\,dx \\&= \int_{D_1} f(x)\,dx+\int_{D_2}f(x)\,dx.\end{aligned}$
3. $f(x)\le g(x)\; (x\in D)$ とするとき，
  $\int_{D} f(x)\,dx\le \int_D g(x)\, dx.$
4. $D_1\subset D$ とするとき，
  $\int_{D_1} f(x)\,dx = \int_D 1_{D_1}(x)f(x)\,dx.$
$D= [a_1,b_1]\times\dots \times [a_n,b_n]$ とし， $h \colon D\to \mathbb{R}$ が $D$ 上連続関数であれば， $D$ 上可積分である。