スカラー行列とは,単位行列を用いて A=aI_n のように書ける行列のことで,まるでスカラーのように扱える行列を指します。これについて,定義と大事な性質を1つ紹介しましょう。
スカラー行列の定義
定義(スカラー行列)
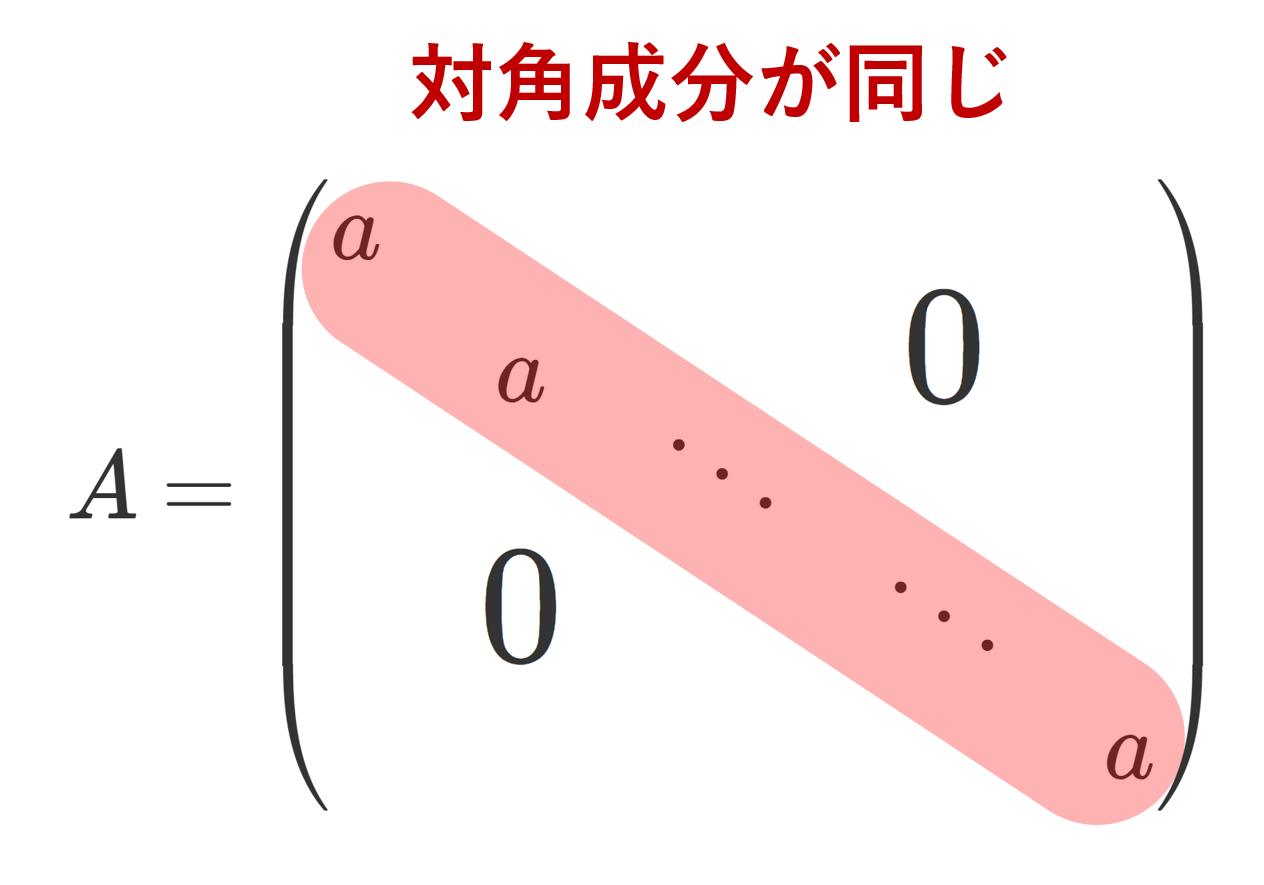
\large \color{red} A=\begin{pmatrix} a \\ & a&& \huge{0} \\ & & \ddots \\ &\huge{0}&& \ddots \\ &&&& a \end{pmatrix}
のように,対角成分以外は全て 0 で,対角成分は全て等しい行列をスカラー行列 (scalar matrix) という。
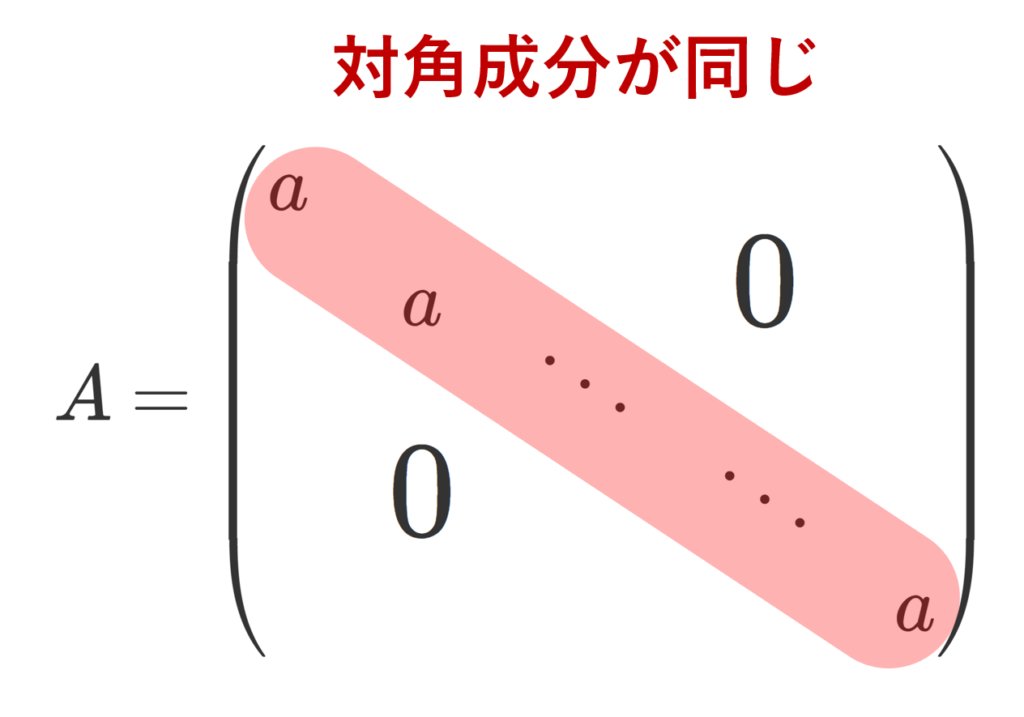
特に,n 次正方行列がスカラー行列のとき,n 次スカラー行列といいます。
スカラー行列とは要するに単位行列の定数倍の行列,すなわち \color{red} A = aI_n のような行列を指します。「スカラー行列」という名前は,ほぼスカラー(定数)のように扱える行列だということです。
スカラー行列の大事な性質
定理(スカラー行列の性質)
A を n 次スカラー行列とする。このとき,任意の n 次正方行列 B に対して,
\large \color{red}AB=BA
が成り立つ。逆に,これが任意の n 次正方行列 B について成り立つならば, A はスカラー行列である。
前半はほぼ自明でしょう。「逆に,」以降の方が大事です。よって後半を証明していきましょう。
後半の証明
A=(a_{ij}) とする。
B を (j,i) 成分のみ 1 でそれ以外が 0 の行列とする ( B=E_{ji} 行列単位)。このとき,
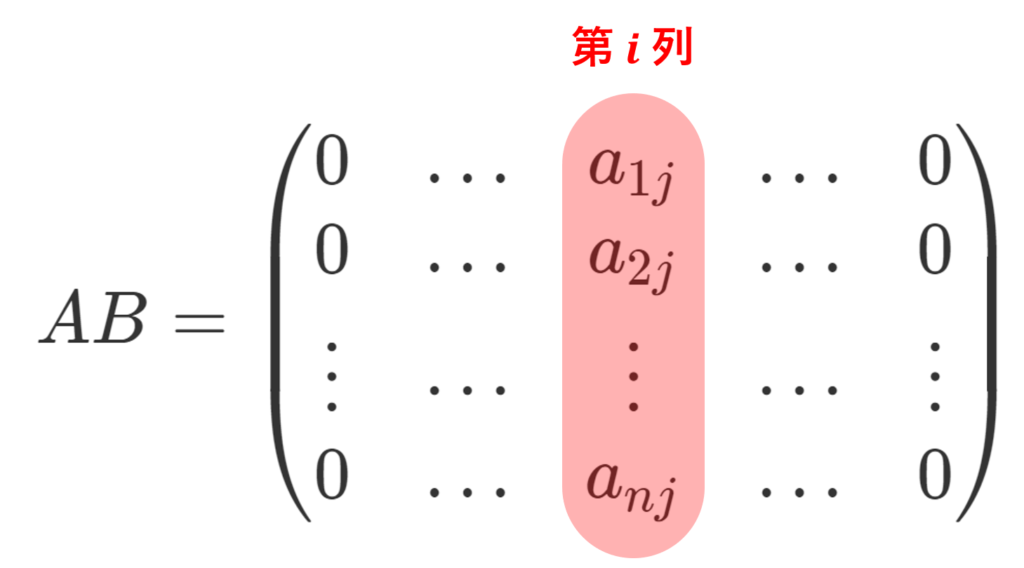
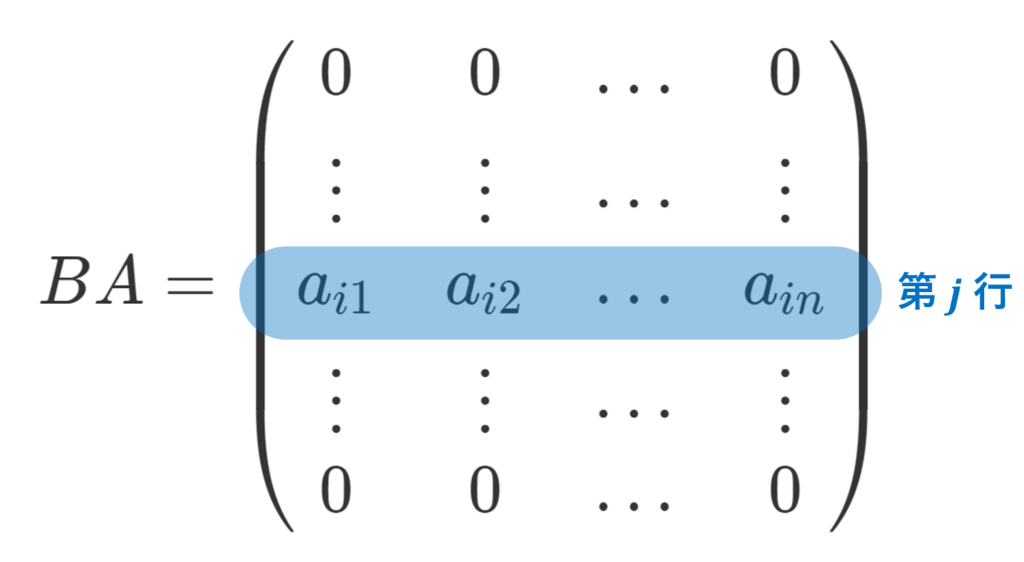
であり, AB = BA なので,
かつ a_{ii} =a_{jj} である。i,j を任意に動かすことで, k\ne l のとき, a_{kl}=0 であり,また
なので, A はスカラー行列である。
証明終
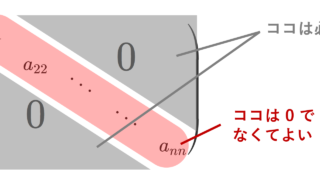
なお,スカラー行列は対角行列の1つですから,対角行列の性質がすべて成立します。対角行列の性質は以下で解説しています。