測度論・関数解析における本質的上限・本質的下限(esssup, essinf)とは,零集合を無視した上限・下限のことを言います。本質的上限・本質的下限について,ちゃんとした定義と具体例・性質を挙げましょう。
本質的上限・本質的下限(esssup,essinf)
\R には標準的なルベーグ測度が入っているものとします。
定義(本質的上限・本質的下限)
(X,\mathcal{F}, \mu) を測度空間, f\colon X\to \R を可測関数とする。このとき,
\color{red}\operatorname{ess~sup} f = \inf \{ a\in\R \mid \mu(f>a) =0\}
を本質的上限 (essential supremum) といい,
を本質的下限 (essential infimum) という。ただし, \inf \emptyset =\infty, \; \sup \emptyset =-\infty とする。
もともと,普通の上限・下限 ( \sup, \inf ) は最小上界,最大下界として定義されました(→上限,下限(sup,inf)の定義と最大,最小(max,min)との違い)。要するに,
\begin{aligned} \sup f &= \inf \{ a\in\R \mid \#\{f>a\}=0\} \\ \inf f &= \sup \{ a\in\R \mid \#\{f<a\}=0\} \end{aligned}
でした( \{f>a\} は \{x\mid f(x)>a\} の省略形です)。
本質的上限・本質的下限 ( \operatorname{ess~sup},\operatorname{ess~inf}) はそれの零集合 (零集合とは \mu(A)=0 となる集合 A\in\mathcal{F} のこと) を除いたバージョンといえますね。
本質的上限・本質的下限(esssup,essinf)の例
例を見るのが最も分かりやすいでしょう。引き続き,\R には標準的なルベーグ測度が入っているものとします。
例1.
f\colon [-1,1]\to \R を
f(x)=\begin{cases} -x^2 & \text{if } x\in [-1, 1]\setminus \{0\}, \\ 1& \text{if } x=0 \end{cases}
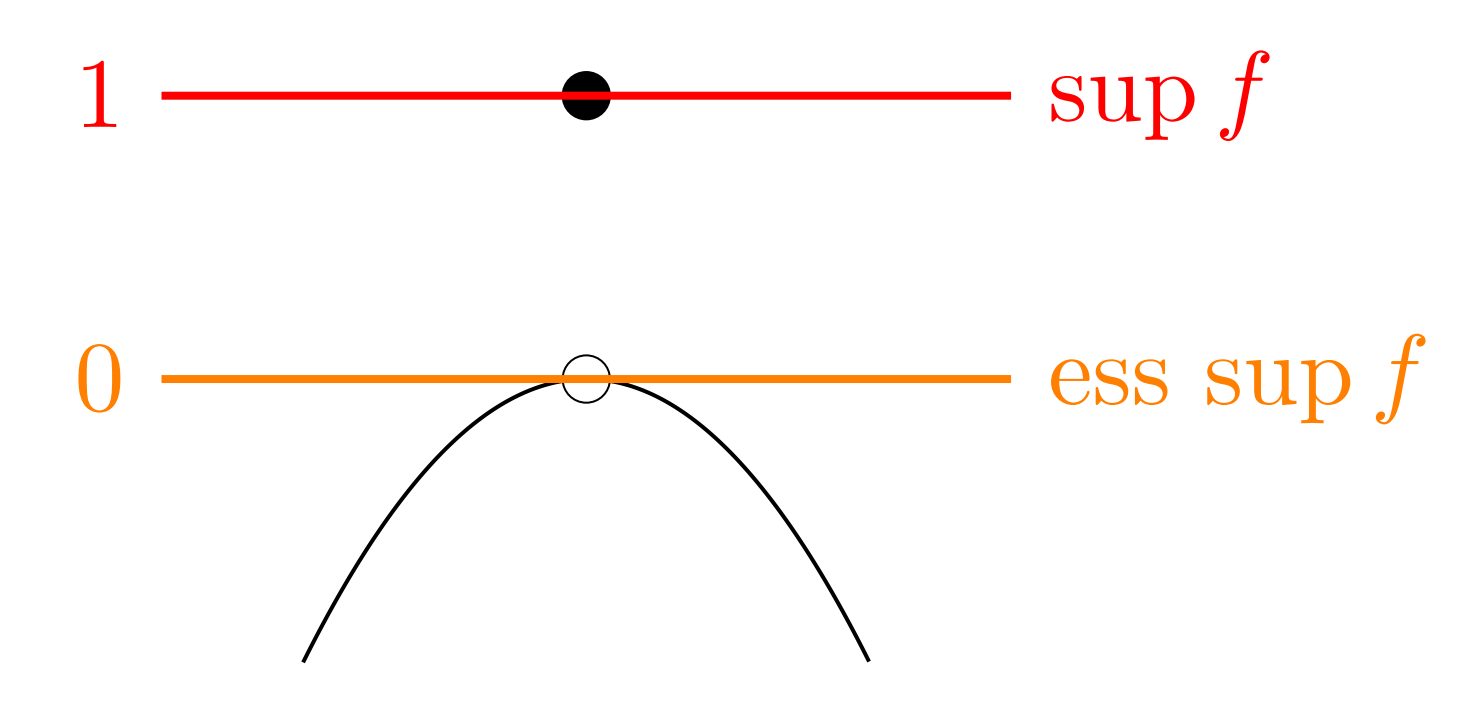
とすると, \color{red}\sup f =1, \; \operatorname{ess~sup} f = 0 である。
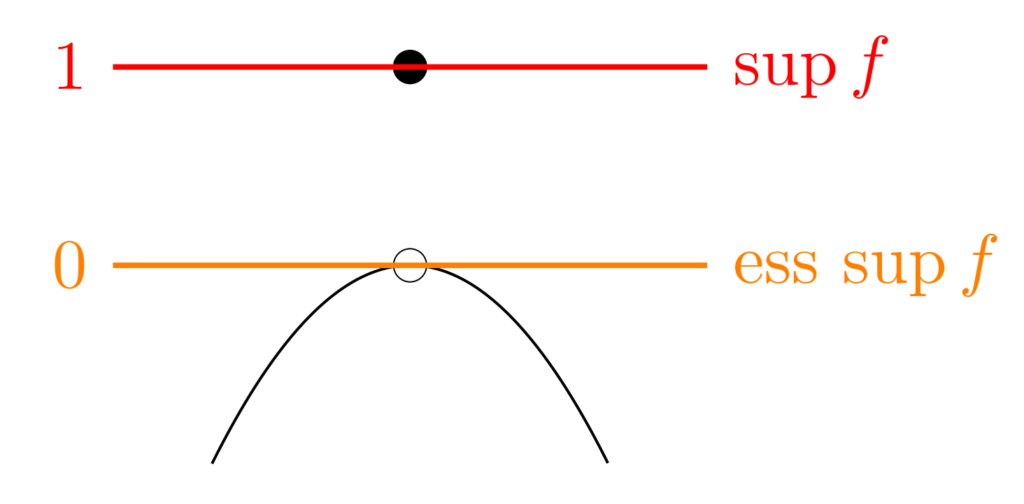
x=0 のところの値だけ「離れて」いるので,上限(sup)は大きくなります。一方で零集合を無視できる本質的上限(esssup)については値が一つだけ離れていようと無視できますから,本質的上限は f(x)=-x^2 のそれと同じです。
また,この例において, \inf f = \operatorname{ess~inf} f= -1 です。
例2.
f\colon \R\to\R を
1_\mathbb{Q}(x)=\begin{cases} 1 & x\in \mathbb{Q},\\ 0 & x \in \R\setminus \mathbb{Q}\end{cases}
と定義する(ディリクレ関数という)。このとき, \color{red}\sup f =1, \; \operatorname{ess~sup} f = 0 である。
\mathbb{Q}\subset \R は零集合ですから,本質的上限を考えるときは,有理数上の値は無視できるわけですね。
また,この例において, \inf f = \operatorname{ess~inf} f= 0 です。
例3.
f\colon (0,\infty)\to \R を f(x)=1/x で定義する。このとき,
\color{red} \begin{gathered}\sup f = \operatorname{ess~sup} f= \infty, \\ \inf f = \operatorname{ess~inf} f= 0 \end{gathered}
である。
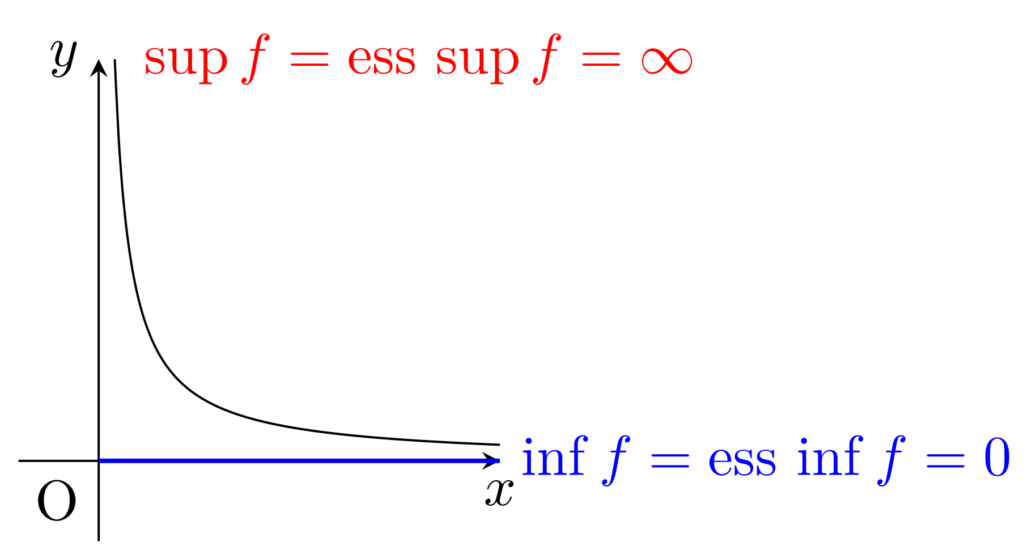
本質的上限・本質的下限(esssup,essinf)の性質
性質をいくつか列挙しておきましょう。
定理(本質的上限・本質的下限の性質)
(X,\mathcal{F}, \mu) を測度空間, f\colon X\to \R を可測関数とする。このとき,
- \operatorname{ess~sup} f = -\operatorname{ess~inf} (-f).
- \inf f\le \operatorname{ess~inf} f \le \operatorname{ess~sup} f \le \sup f.
- g\colon X\to \R も可測関数で, f=g, \;\text{a.e.} (ほとんどいたるところ)とするとき, \operatorname{ess~sup} f=\operatorname{ess~sup} g.
- h\colon \R\to\R が連続関数であるとき, \operatorname{ess~sup} h=\sup h ,\;\operatorname{ess~inf} h= \inf h.
1,2.はほぼ明らかでしょう。3.については,常に \mu(f>a)=\mu(g>a) が成り立つため,成立します。4.も連続関数の性質を考えれば証明可能です。