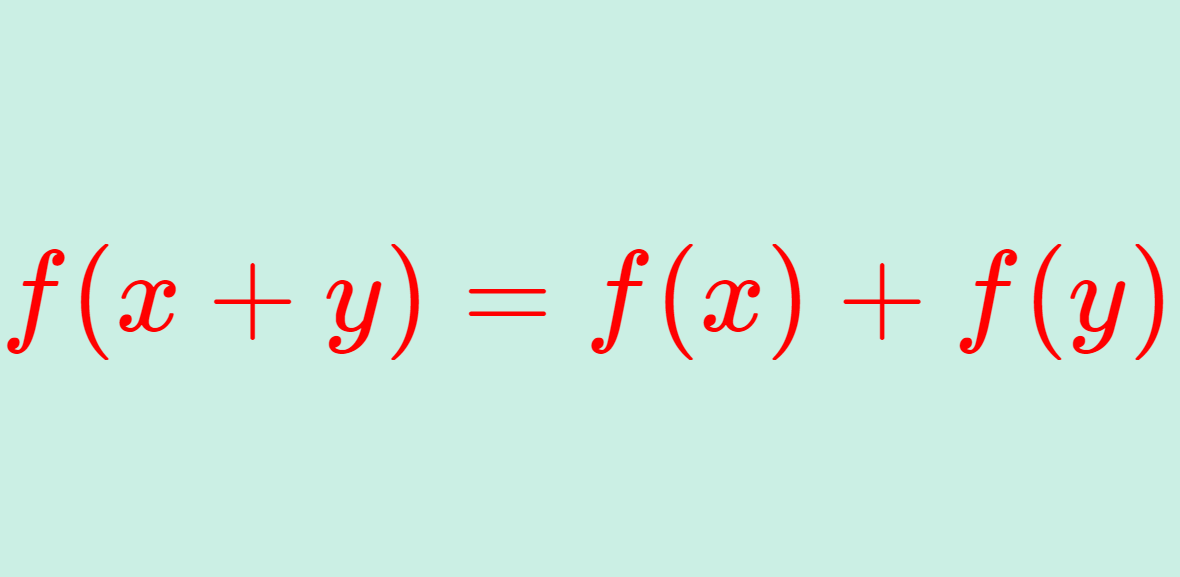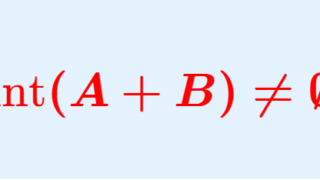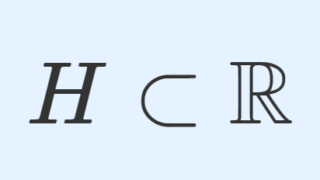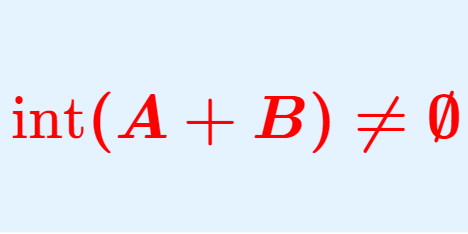コーシーの関数方程式 (Cauchy’s functional equation) とは， f(x+y)=f(x)+f(y) となる関数方程式のことを言います。これの解 f を求め，さらにその関連である関数方程式の解を求めましょう。
【f(x+y)=f(x)+f(y)】コーシーの関数方程式とは
定義（コーシーの関数方程式）
f\colon \R\to\R を関数とする。
\color{red} f(x+y)=f(x)+f(y)\quad x,y\in \R
をみたすとき，これをコーシーの関数方程式 (Cauchy’s functional equation) といい， f を加法的関数 (additive function) という。
これは非常に有名な関数方程式です。さて，この方程式を解く方法を考えましょう。
定義より， f(0+0)=f(0)+f(0) なので， f(0)=0 ですね。
まず，有理数上で解き，その上で実数全体での解を求めます。
有理数上のコーシーの関数方程式
定理1（有理数上のコーシーの関数方程式）
コーシーの関数方程式
\color{red}f(x+y)=f(x)+f(y),\quad x,y\in \R
をみたす関数 f\colon \R\to\R は q\in \mathbb{Q} のとき，\color{red} f(qx)=qf(x)\;(x\in\R) と表せる。
特に， c=f(1) とすれば， \color{red}f(q)=cq である。
特に， f(x+y)=f(x)+f(y),\quad x,y\in\mathbb{Q}
となる f\colon \mathbb{Q}\to \R は f(x)=cx\;(x\in\mathbb{Q}) に限ることになりますね。
この証明は非常に基本的で，大事です。テクニックとして抑えておくとよいです。
証明
以下， x\in\R を任意の実数とする。
Step1：まず正の整数 n\in\mathbb{N} に対し， f(nx)=nf(x) を示す。
f の加法性より，
\begin{aligned}f(nx)&=f(x)+f((n-1)x)\\&= 2f(x)+f((n-2)x)\\ &= 3f(x)+f((n-3)x)\\ &\;\;\vdots \\ &= nf(x) \end{aligned}
であるから，Step1が示せた。
Step2：次に整数 n\in\mathbb{Z} に対し， f(nx)=nf(x) を示す。
n>0 とすると，
\begin{aligned}f(nx)+f(-nx) &= f(nx+(-nx)) \\&= f(0)=0\end{aligned}
より， f(-nx)=-f(nx) である。これとStep1より，
であるから，Step2が示せた。
Step3：整数 m\ne 0 に対し，\displaystyle f\left(\frac{x}{m}\right) = \frac{f(x)}{m} を示す。
Step2で得られた式 f(nx)=nf(x) の n を m に， x を x/m に置き換えると，
f\left(m\cdot \frac{x}{m}\right)=mf\left(\frac{x}{m}\right)
である。すなわち， f(x)=mf(x/m) なので， f(x/m)=f(x)/m である。
Step4：最後に，有理数 q\in\mathbb{Q} に対し， f(qx)=qf(x) を示す。
q=n/m \;(m,n\in\mathbb{Z},\, m\ne 0) と定める。Step2で得られた式 f(nx)=nf(x) の x を x/m に置き換えて適用した後に，Step3で得られた式 f(x/m)=f(x)/m を適用すると，
f\left(\frac{n}{m}x\right)= nf\left(\frac{1}{m} x\right) = \frac{n}{m}f(x)
となって，結局題意は示された。
証明終
「正の整数 → 整数 → 1/mの形 → 有理数」のように，順々に広げる形で証明できましたね。この証明は，何も見ないで出来るようにしておいた方が良いと思います。
実数上のコーシーの関数方程式
さて，上では x\in\mathbb{Q} のとき， f(x)=cx と表せることを示しました。これを x\in\R に拡張しましょう。
定理2（実数上のコーシーの関数方程式）
コーシーの関数方程式
\color{red}f(x+y)=f(x)+f(y),\quad x,y\in \R
をみたす関数 f\colon \R\to\R が以下のいずれかをみたすとする。
このとき， c=f(1) とすると，\color{red} f(x)=cx と表せる。
一方で，以上のいずれも仮定せず，選択公理を認めると， f は f(x)=cx 以外に無数に存在する。
1.～3.の証明は理系大学生なら理解できると思います。4.と一番最後の話は，少し専門的な数学の知識が必要です。順番に見ていきましょう。
1. ある1点で連続なら f(x)=cx
証明
まず， f がある1点で連続なら，連続関数であることを示す。 f が x=a で連続であるとすると，任意の点 b\in \R に対し， f の加法性より，
\begin{aligned} f(b+h)-f(b)&= f(h)\\ &= f(a+h)-f(a)\\&\xrightarrow{h\to 0} 0 \end{aligned}
となる。よって f が連続関数であることが示せた。
前節で， \mathbb{Q} 上 f(x)=cx であることは示せており，\mathbb{Q} は \R 上稠密であるから， f の連続性より， f(x)=cx \; (x\in\R) となる。
証明終
2. ある区間で単調なら f(x)=cx
証明
f が区間 (a,b) 上広義単調増加であるとする。 x\in (a,b) に対し，
- a<p_1<p_2<\dots < x かつ p_n\to x となる有理数列 \{p_n \}\subset \mathbb{Q} と
- x<\dots < q_2<q_1<b かつ q_n\to x となる有理数列 \{q_n\}\subset \mathbb{Q}
をとる。 f の単調性と， f(x)=cx \; (x\in\mathbb{Q})より，
cp_n= f(p_n)\le f(x)\le f(q_n)=cq_n
が成り立ち，各辺 n\to\infty とすることで， f(x)=cx がわかる。x\in (a,b) なら f(x)=cx が結論付けられたので， f は (a,b) 上連続であり，1.に帰着できる。
証明終
なお，関数が単調なら，不連続点は高々可算個であることが知られています(→【Frodaの定理】単調関数の不連続点は高々可算個であることの証明)。これを用いると，単調な関数には，少なくとも一つの連続点が存在しますから，1.に帰着して証明することができますね。これでも構いません。
3. ある区間で有界なら f(x)=cx
ある点で連続なら当然その点の周りのある区間で有界ですし，ある区間で単調なら，当然その区間に含まれる有界区間が取れますから，本項目3.は1,2.よりも条件が弱く，より一般的なことを言っています。
証明
f(x) は [a,b] 上有界であるとする。このとき， x\in [a,b] 上 |f(x)|\le M かつ |a|<M かつ |b|<M となる M>0 がとれる。
x\in \R とする。正の整数 n\in\mathbb{N} に対し， nx-b<q_n<nx-a となる有理数列 \{q_n\}\subset \mathbb{Q} をとる。このとき， nx-q_n\in [a,b] である。 f の加法性と定理1から，
\begin{aligned} |f(x)-cx| &=\frac{1}{n}|nf(x)-cnx| \\ &= \frac{1}{n}| f(nx)-cnx|\\ &= \frac{1}{n}|f(nx-q_n)+f(q_n)-cnx|\\ &= \frac{1}{n} |f(nx-q_n)+cq_n-cnx|\\ &\le \frac{1}{n}( |f(nx-q_n)| +|c||q_n-nx|)\\ &\le \frac{1}{n} (M+|c|M)\\ &\xrightarrow{n\to\infty} 0 \end{aligned}
となるから， f(x)=cx である。
証明終
4. 可測なら f(x)=cx
証明
f\colon \R\to\R を可測とし， \mu をルベーグ測度とする。 n\in\mathbb{Z} に対し，
A_n = \{x\in\R\mid n\le f(x)< n+1\}
とおくと， \{A_n\} はどの2つも共通部分を持たず， \bigcup_{n\in\mathbb{Z}} A_n=\R であるから， \mu(A_{n_0})>0 となる n_0\in\mathbb{Z} が存在する。
A_{n_0} 上 n_0\le f< n_0+1 であるから， A_{n_0} 上 f は有界である ( |f|\le |n_0|+1 とできる)。ここで， a,b\in A_{n_0} とすると，
\begin{aligned}|f(a+b)|&=|f(a)+f(b)|\\&\le |f(a)|+|f(b)|\\&\le 2|n_0|+2\end{aligned}
であるから， f は A_{ n_0}+A_{n_0} = \{a+b\mid a,b\in A_{n_0}\} 上も有界である。シュタインハウスの定理より， A_{n_0} +A_{n_0} は区間を含むから，3.に帰着できる。
証明終
シュタインハウスの定理を用いることで，簡単に証明できましたね。シュタインハウスの定理の証明は以下で行っています。
1～4のいずれも仮定せず，選択公理を認めた場合
連続性・単調性・有界性・可測性のいずれも仮定せず，選択公理を認めた場合は，コーシーの関数方程式の解は無数にあることが知られています。
\R を \mathbb{Q} 上のベクトル空間とみなして，その上の基底を考えます。この基底をハメル基底 (Hamel basis) といい，選択公理を認めることで，その存在が証明できます。すなわち，ハメル基底 H\subset \R とは以下のようなものです。
- 任意の有限個の h_1,h_2,\dots, h_n \in H と q_1,q_2,\dots, q_n \in\mathbb{Q} に対し，
とできる H\subset \R のことをハメル基底 (Hamel basis) という。
詳しくは，以下で解説しています。
いま，ハメル基底を H\subset \R としましょう。
コーシーの関数方程式は， f(x+y)=f(x)+f(y) に加えて，定理1 で示したように， q\in\mathbb{Q} に対し， f(qx)=qf(x)\;(x\in\R) も満たします。したがって，\R を \mathbb{Q} 上ベクトル空間とみなすと， f\colon \R\to\R はその上の線形写像になります。
線形写像は基底の行先を決めるだけで，すべての元の行先が決まります。（これは【表現行列】線形写像の行列表示を詳しくの最初の方でも軽く解説しています）ゆえに，関数 g\colon H\to \R を決めれば，線形写像 f\colon \R\to\R が一意に決まります。逆に言うと， g\colon H\to \R の数だけ， f\colon \R\to\R が作れるということです。
g\colon H\to \R の作り方は無数にありますから， f も無数にあるということになります。
コーシーの関数方程式の関連
コーシーの関数方程式に帰着させることで，以下の関数方程式の解も求めることが可能です。簡単のため，関数 f には連続性を課すことにしましょう。有界性や単調性，可測性を課しても同様です。
定理（コーシーの関数方程式の関連）
f\colon \R(\text{ or } (0,\infty) )\to \R を連続関数とする。このとき，
- f(x+y)=f(x)f(y) かつ f(x)>0 の解は \color{red}f(x)=e^{cx}, \;c,x\in\R である。
- f(xy)=f(x)+f(y), \; x,y>0 の解は \color{red}f(x) = c\log x,\; c\in\R,x>0 である。
- f(xy) =f(x)f(y),\; x,y>0 かつ f(x)>0 の解は \color{red} f(x) = x^c ,\; c\in\R,x>0 である。
簡単に証明しておきましょう。
証明
1. f(x+y)=f(x)f(y) について
\color{red}g(x)=\log f(x) とすると， g(x+y)=g(x)+g(y) になるから， g はコーシーの関数方程式をみたす。 g は連続より， g(x)=cx. ゆえに， f(x)=e^{g(x)}=e^{cx}.
2. f(xy)=f(x)+f(y) について
\color{red} g(x)=f(e^x) とおくと， g(x+y)=g(x)+g(y) になるから， g はコーシーの関数方程式をみたす。 g は連続より， g(x)=cx. ゆえに， f(x)=g(\log x)=c\log x.
3. f(xy)=f(x)f(y) について
\color{red} g(x)=\log f(e^x) とおくと， g(x+y)=g(x)+g(y) になるから， g はコーシーの関数方程式をみたす。 g は連続より， g(x)=cx. ゆえに， f(x)=e^{g(\log x)}=e^{c\log x}=x^c.
証明終
