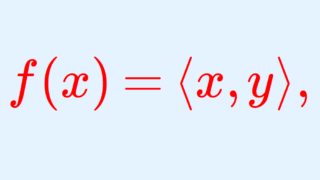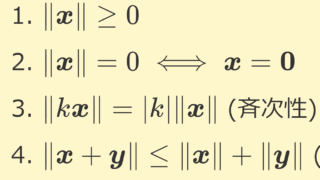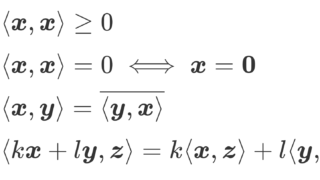ヒルベルト空間とは,内積が定義されていて,かつ完備(敷き詰まっている)空間のことを言います。ヒルベルト空間の定義を確認し,関数解析でよく用いられる具体例と基本的性質を述べましょう。
ヒルベルト空間とは
本記事では,ベクトル空間は全て \mathbb{C} 上で考えます。
「完備」とは,イメージでいうと「隙間なく敷き詰まっている」ということであり,厳密にいうと,「任意のコーシー列が収束列になる」ということです。「内積空間」とは,内積が定まっているベクトル空間のことを言います。
関数解析には,ノルム空間・内積空間・バナッハ空間・ヒルベルト空間というさまざまな空間が現れますが,関係性をまとめておきましょう。

それぞれの空間の解説は,以下で行っています。特に,定義が意味不明の場合はバナッハ空間の記事である程度,基本的な概念の復習を行っていますので,それを参照してください。バナッハ空間に内積が定まる空間がヒルベルト空間です。
ノルム空間・内積空間・バナッハ空間・ヒルベルト空間の中では,ヒルベルト空間が最も「性質の良い」空間であることが分かりますね。ヒルベルト空間は,完備でかつ直交性を考えることができるため,数学的に非常に扱いやすい空間です。
また,物理において,たとえば量子力学を勉強する際にも出てくる空間でしょう。
代表的なヒルベルト空間
ここでは,関数解析で扱う代表的なヒルベルト空間を紹介します。
例1(数列空間 \ell^2).
\ell^2 を \sum_{n=1}^\infty |a_n|^2<\infty となる複素数列 \{a_n\} 全体の集合とする。このとき, a=\{a_n\}, b=\{b_n\}\in \ell^2 に対し,その内積を
\begin{equation} \langle a,b\rangle = \sum_{n=1}^\infty a_n \overline{b_n}\end{equation}
と定めると, \ell^2 はヒルベルト空間になる。
1\le p<\infty に対し, \sum_{n=1}^\infty |a_n|^p<\infty となる複素数列 \{a_n\} 全体の集合を \ell^p とします。このとき, a=\{a_n\}\in\ell^p に対し,
\|a\|_p =\left(\sum_{n=1}^\infty |a_n|^p\right)^{1/p}
とすると,これは完備なノルム空間,すなわちバナッハ空間になります。特に, p=2 のときは,上の (1) 式の内積を定義でき,ヒルベルト空間になります。
例2(関数空間 L^2).
L^2 を \int_\R |f(x)|^2\, dx<\infty となる可測関数 f\colon \R\to \mathbb{C} 全体の集合(をa.e.の元で同一視したもの)とする。このとき, f,g\in L^2 に対し,その内積を
\begin{equation} \langle f,g\rangle = \int_\R f(x) \overline{g(x)}\, dx\end{equation}
と定めると, L^2 はヒルベルト空間になる。
1\le p<\infty に対し, \int_\R |f(x)|^p\, dx <\infty となる可測関数 f\colon\R\to\mathbb{C} 全体の集合(をa.e.の元で同一視したもの)を L^p とします。このとき,f\in L^p に対し,
\|f\|_p =\left(\int_\R |f(x)|^p\,dx\right)^{1/p}
とすると,これは完備なノルム空間,すなわちバナッハ空間になります。特に, p=2 のときは,上の (1) 式の内積を定義でき,ヒルベルト空間になります。
例1.と類似点が多いのが分かるでしょうか。関数解析では,この空間もよく考えます。
例3(ソボレフ空間 H^s ).
s\ge 0 を実数とする。 H^s を,例2.で用いた L^2 を用いて,
H^s = \{ f\in L^2\mid \widehat{f}(\xi)(1+|\xi|^2)^{s} \in L^2\}
と定める。ただし, \widehat{f} は f のフーリエ変換を表す。 f,g\in H^s に対し,内積を
と定めると, H^s はヒルベルト空間になる。
H^s の空間に属する関数は,ある程度の「滑らかさ」をもっており, s は滑らかさを表すある種の指標になっています。この空間では,ある種の「微分」を考えることができるようになり,微分方程式の解を求めるのにも活用されます。
ヒルベルト空間の性質
定理1(ヒルベルト空間の性質1)
1.はほぼ明らかでしょう。逆に,閉でない部分空間はヒルベルト空間にならないことに注意してください。1.の証明が分からない場合は,バナッハ空間とは~定義と具体例5つ~の記事内で似たような証明を行っていますので,それを参照してください。
2.も,有限次元ノルム空間が完備であることから直ちに従います。これも,バナッハ空間とは~定義と具体例5つ~内で証明しています。
3.のみ略証しておきましょう。ヒルベルト空間が初めての場合は,意味が分からないかもしれませんので,飛ばして大丈夫です。
3.の略証
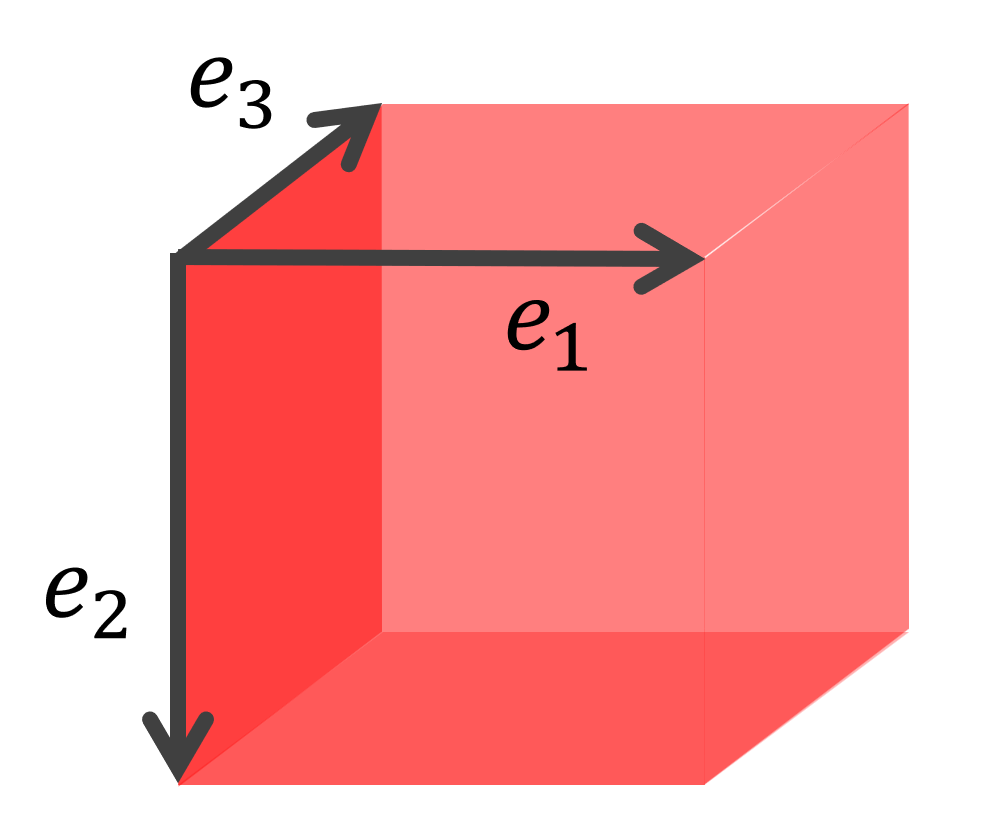
可分な無限次元ヒルベルト空間 X には,可算個の元からなる正規直交基底が取れる(シュミットの直交化法を用いれば明らかだが,詳細は省略する)。それを \{x_n\}\subset X としよう。
e_n \in \ell^2 を e_n = (0,\dots, 0, 1, 0,\dots ) (第 n 成分のみ 1 )と定め,T\colon x_n\mapsto e_n となる線形作用素 T\colon X\to \ell^2 をとると,これは等長であり,ユニタリ作用素になることが分かる。
証明終
以下は,リースの表現定理 (Riesz representation theorem) と呼ばれる定理です。ヒルベルト空間の大事な性質の一つです。
定理2(ヒルベルト空間の性質2)
H をヒルベルト空間とする。 f\colon H\to \mathbb{C} を有界線形汎関数とすると,ある x\in H が存在して,
f(y) = \langle y, x\rangle,\quad y\in H
と表せる。したがって,特にヒルベルト空間は回帰的(反射的)である。
H 上の有界線形汎関数は,ある意味 H の元を用いて表現できるということですね。
証明は,以下で行っています。