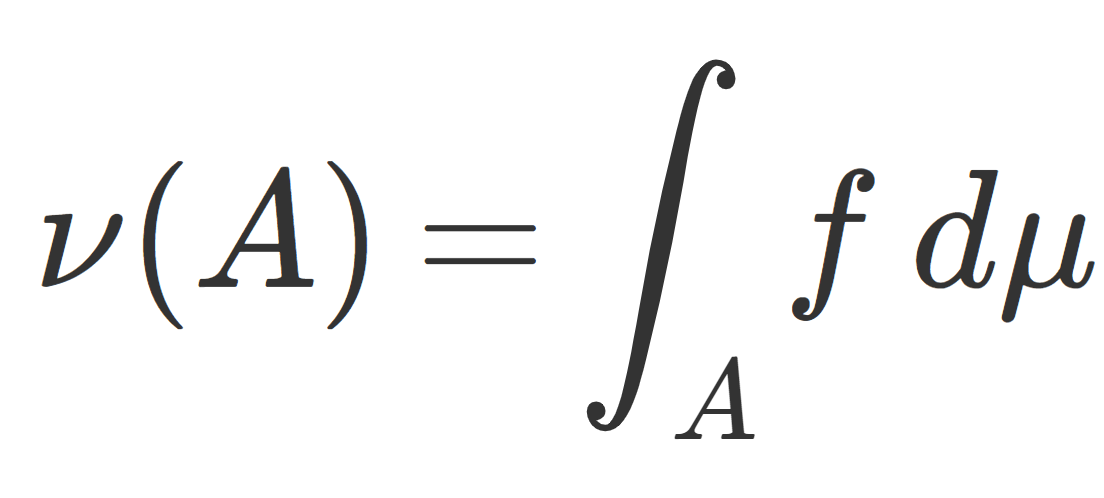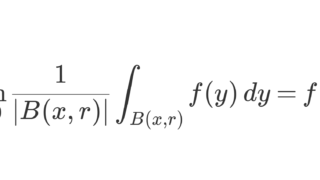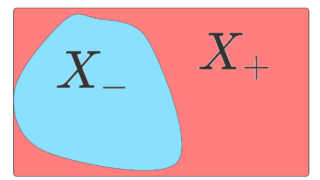ラドンニコディムの定理と呼ばれる,測度論における「微分」を扱う定理を紹介しましょう。
これは確率論における条件付き期待値にも使われる概念であり,とても重要です。
ラドンニコディムの定理
ラドンニコディムの定理 (Radon–Nikodym theorem)
(X,\mathcal{F}) を可測空間, \mu,\nu をその上のσ有限な測度とする。さらに \nu が \mu に関して絶対連続(\color{red}\nu \ll \mu)とする。このとき, \mu に関して局所可積分な非負関数 f\in L^1_{\mathrm{loc},+}(\mu) が(\mu–a.e.の意味で)一意的に存在して,
\color{red}\nu(A)=\int_A f \, d\mu,\quad A\in \mathcal{F}
とかける。このときの f を \color{red} \dfrac{d\nu}{d\mu} とかき,ラドンニコディム密度 (Radon-Nikodym density) またはラドンニコディム微分 (Radon-Nikodym derivative) という。
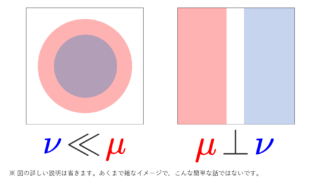
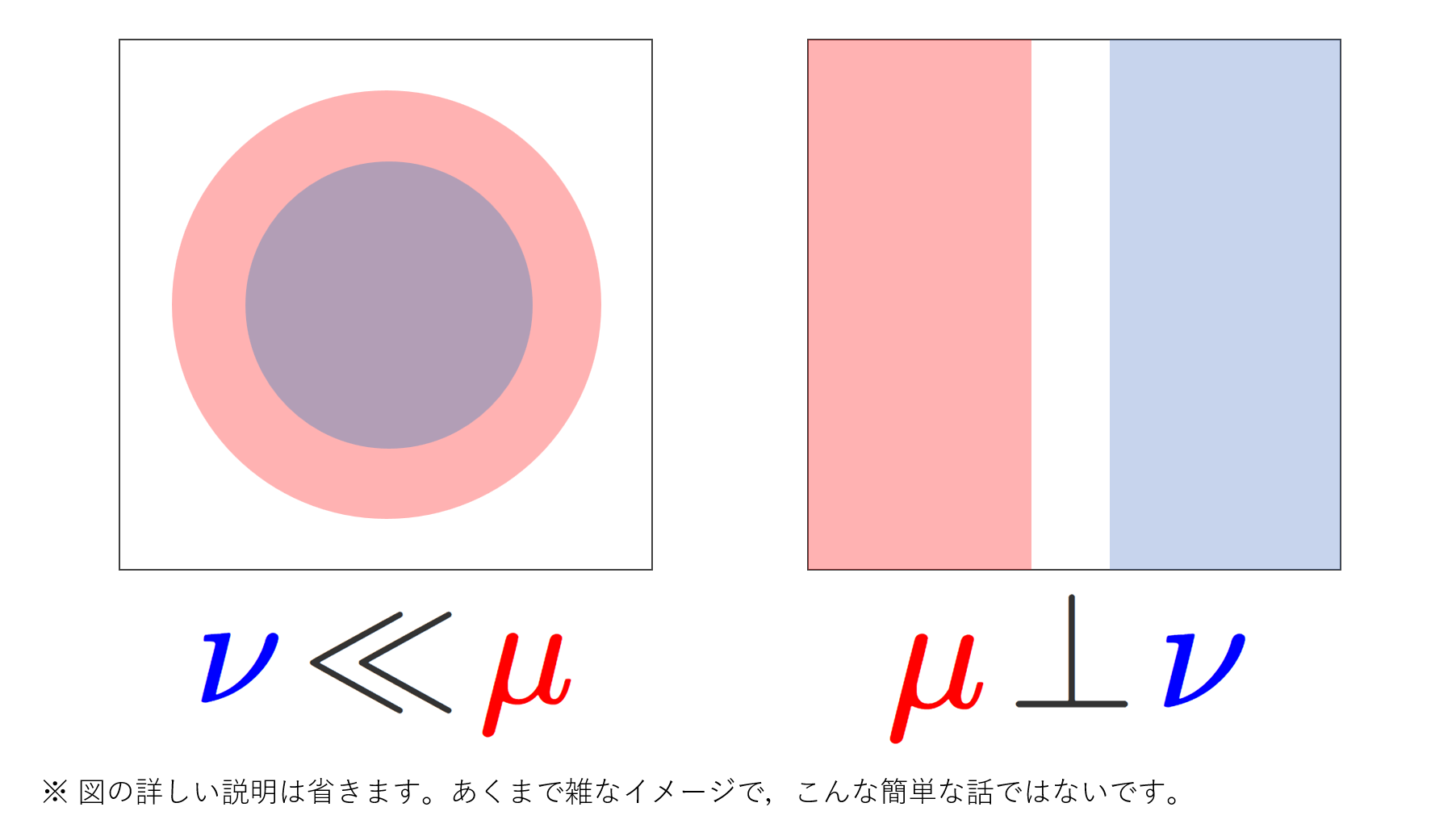
\nu が \mu に関して絶対連続 (absolutely continuous) とは, \mu(A)=0\implies \nu(A)=0 が成り立つことです(→測度の絶対連続性・同値性・特異性とルベーグ分解)。
f が局所可積分 (locally integrable) とは, A\in\mathcal{F} が \mu(A)<\infty をみたすならば \int_A |f|\ d\mu<\infty をみたすということです。
なお,\mu,\nu がσ有限な測度というのは,本定理の本質です。実際, (\R, \mathcal{B}(\R)) 上の数え上げ測度を \#,ルベーグ測度を \mu とすると,数え上げ測度はσ有限ではなく,一方 \mu \ll \# は成立します。このとき,もし f\in L^1_{\mathrm{loc},+}(\#) で
\mu(A)= \int_A f \, d\#
をみたすものが存在したとすると, A=\{a\} とすることで, f(a)=0 となりますが,これだと \mu が零測度になってしまい矛盾してしまいます。
ラドンニコディムの定理の2通りの証明
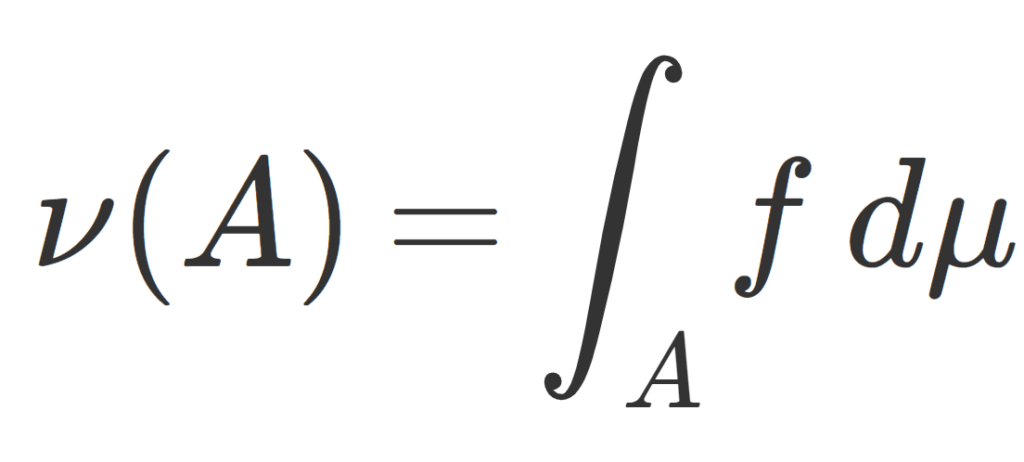
ラドンニコディムの定理の証明を,
- 測度論を用いた証明
- 関数解析を用いた証明
の2通り紹介しましょう。
1. 測度論を用いた証明
測度論を用いた証明
一意性は【数学科向け】ルベーグ積分の定義を段階を踏んで解説するの定理A.5より明らかなので,存在について示す。
まず,\mu,\nu を有限測度とする。
F=\left\{ g \in L_+^1(\mu) \middle| \forall A\in \mathcal{F}, \int_A g\, d\mu\le \nu(A) \right\}
とする。 0\in F より, F\ne \emptyset である。ここで, g_1, g_2\in F とすると, \max\{ g_1, g_2\}\in F である。実際,任意の A\in\mathcal{F} に対し,
であるからである。ここで, \{g_n\} \subset F を
となるように定める。 f_n =\max\{ g_1, g_2, \dots, g_n\} とすると, \{ f_n\}\subset F は増大列であり,
である。 f=\lim_{n\to\infty } f_n と定めると,単調収束定理より,
であり,さらに同じ定理から f\in F もわかる。ここで, f が求めるものであることを背理法で示す。ある A\in \mathcal{F} で,\int_A f\, d\mu < \nu(A) を仮定する。このとき,\int_X f\, d\mu < \nu(X) である。 そこで,
として測度 \nu_0 を定義する。\nu_0(X)>0 であるから,ある \varepsilon >0 が存在して, \nu_0(X)>\varepsilon \mu(X) とできる。符号付き測度 \nu_0-\varepsilon \mu におけるハーンの分解を X=X_+\cup X_- とする。 (\nu_0-\varepsilon\mu)(X)>0 より, (\nu_0-\varepsilon\mu)(X_+)>0 である。このとき, A\in\mathcal{F} に対し, \nu_0(A\cap X_+)\ge \varepsilon \mu(A\cap X_+) であり,
なので, f+\varepsilon 1_{X_+}\in F である。 \mu(X_+)=0 とすると,絶対連続性より \nu(X_+)=0 となって, (\nu_0-\varepsilon\mu)(X_+)>0 に矛盾する。したがって, \mu(X_+)>0 であり,
であるが,これは矛盾している。よってやはり f が求めるものである。
\mu, \nu がσ有限のとき
全体空間 X をどの2つも互いに素な \{X_n\} で, \mu(X_n),\nu(X_n)<\infty となるものに分割して同様のことを考えればよい。
証明終
2. 関数解析を用いた証明
実ヒルベルト空間論を用いた証明も紹介しておきましょう。関数解析の知識が必要です。
関数解析を用いた証明
一意性は【数学科向け】ルベーグ積分の定義を段階を踏んで解説するの定理A.5より明らかなので,存在について示す。
まず,\mu,\nu を有限測度とする。
g\colon X\to \R を g\in L^2(\mu+\nu) とする。コーシーシュワルツの不等式より,
\begin{aligned}&\int|g| \,d(\mu+\nu) \\ &\le \left(\int |g|^2\,d(\mu+\nu) \right)^{1/2} \left(\int 1^2\,d(\mu+\nu) \right)^{1/2} \\ &= \|g\|_{L^2(\mu+\nu)}\sqrt{ (\mu+\nu)(X)}. \end{aligned}
ゆえに L^2(\mu+\nu)\subset L^1(\mu+\nu)\subset L^1(\mu) である。したがって,
によって,線形汎関数 \varphi\colon L^2(\mu+\nu)\to\R が定まり,有界である。 リースの表現定理より,ある f_1\in L^2_+(\mu+\nu) が存在して,
とできる。同様にある f_2\in L^2_+(\mu+\nu) が存在して,
とできる。辺々足し算すると, \int g\, d(\mu+\nu)=\int g (f_1+f_2)\, d(\mu+\nu) となるため, f_1+f_2=1,\, (\mu+\nu)\text{-a.e.} がわかる。ここで,
であり,さらに \nu\ll\mu より (\mu+\nu)(f_1=0)=0 である。したがって, (\mu+\nu)\text{-a.e.} の意味で
と定義できて,任意の g\in L^2(\mu+\nu) で
となる。 g=1_{A} とすることで,結論を得る。
\mu, \nu がσ有限のとき
全体空間 X をどの2つも互いに素な \{X_n\} で, \mu(X_n),\nu(X_n)<\infty となるものに分割して同様のことを考えればよい。
証明終
符号付き測度・複素測度におけるラドンニコディムの定理
ラドンニコディムの定理は,\nu を符号付き測度や複素測度に拡張することが可能です。
ラドンニコディムの定理2 (Radon–Nikodym theorem)
(X,\mathcal{F}) を可測空間, \mu をその上のσ有限な測度,\nu をσ有限な符号付き測度(複素測度)とする。さらに \nu が \mu に関して絶対連続(\color{red}\nu \ll \mu)とする。このとき, \mu に関して局所可積分な実数値関数(複素数値関数) f\in L^1_{\mathrm{loc}}(\mu) が(\mu–a.e.の意味で)一意的に存在して,
\color{red}\nu(A)=\int_A f \, d\mu,\quad A\in \mathcal{F}
とできる。このときの f を \color{red} \dfrac{d\nu}{d\mu} とかき,ラドンニコディム密度 (Radon-Nikodym density) またはラドンニコディム微分 (Radon-Nikodym derivative) という。
符号付き測度がσ有限とは,測度 |\nu|=\nu_++\nu_- がσ有限であることを指し,複素測度がσ有限とは,符号付き測度 \operatorname{Re}\nu , \operatorname{Im} \nu が共にσ有限であるとします(記号は符号付き測度・複素測度の定義と分解定理内のものを用いた)。
証明は,ジョルダンの分解定理により \nu を分解して考えれば明らかです。
測度の微分はラドンニコディム微分
ここまで,
\nu(A)=\int_A f \, d\mu,\quad A\in \mathcal{F}
となる f を d\nu/d\mu とかきました。ここでは, \mu をルベーグ測度としましょう。このとき,以下が成り立つことが知られています。
ここで,\mu(x,x+h)=h です。ラドンニコディム微分は,本当の意味で微分だということですね。詳しくは以下で解説しています。