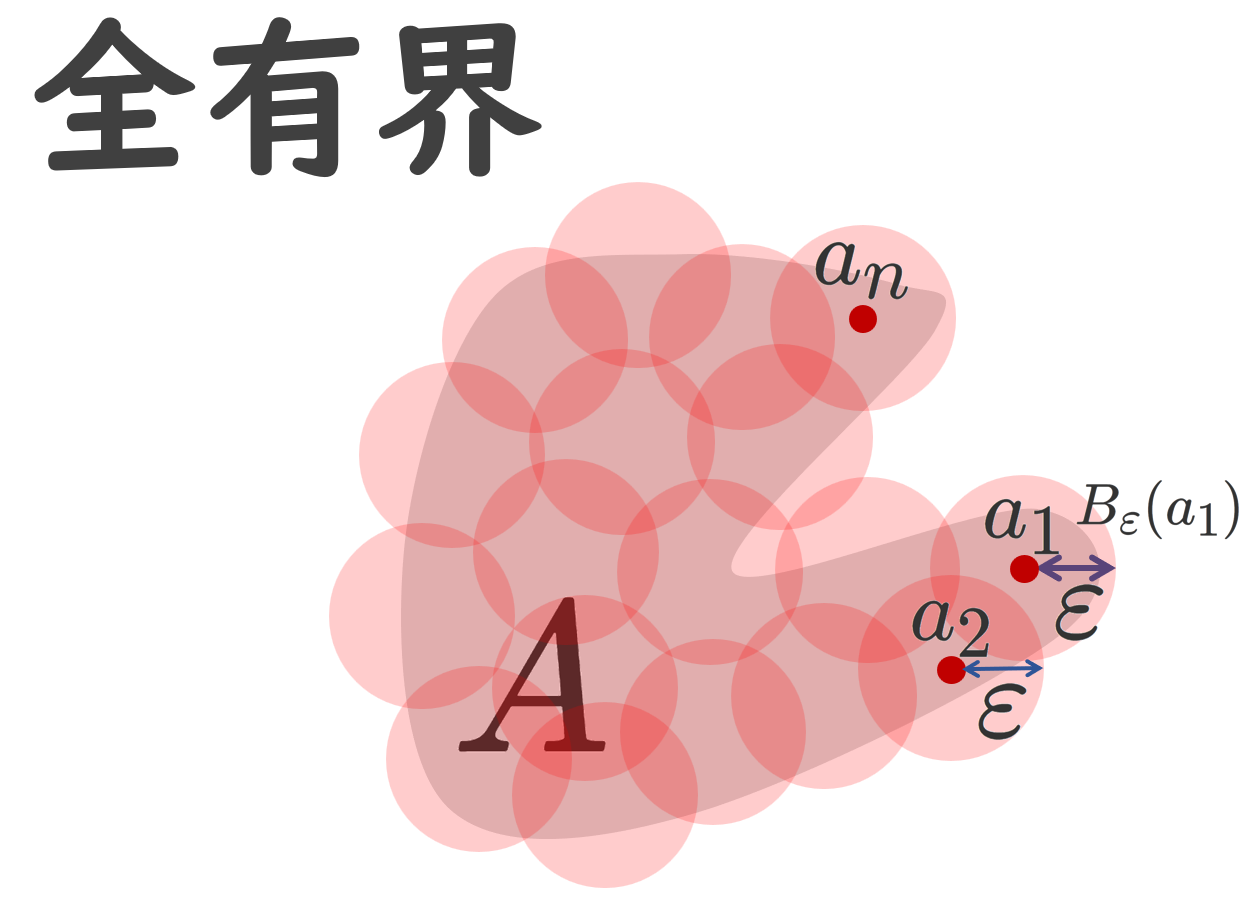
距離空間あるいはその部分集合が全有界であるとは,任意に小さい有限個の円板で,その集合全体が覆えることを言います。
距離空間における全有界性について,有界性との違いを比較しながらその定義・例を理解していきましょう。全有界であれば有界であることの証明も行います。
距離空間における有界性・全有界性
(X,d) を距離空間とし, a\in X に対し, a の \varepsilon -近傍を
\color{red}\large B_\varepsilon (a)=\{x\in X\mid d(a,x)<\varepsilon\}
とかくことにします。簡便にするため,本記事ではこれを a 中心,半径 \varepsilon の円板 (disk)ということにします(広がりが平面なわけではなく,厳密には(次元が定まっていれば d 次元)球体の方が適切でしょう)。
定義(有界・全有界)
(X,d) を距離空間とする。
A\subset X が有界 (bounded) であるとは,ある a\in A と M>0 が存在して,
\Large\color{red} A\subset B_M(a)
とできることをいう。 A\subset X が全有界 (totally bounded) であるとは,任意の \varepsilon >0 に対して,ある n\ge 1 と a_1,a_2,\dots, a_n\in A が存在して,
有界の定義は,ある a\in A と M>0 が存在して, A\subset B_M(a) としましたが,実際は任意の b\in A に対して,ある L>0 が存在して, A\subset B_L(b) とできます。 L=d(a,b)+M とすればよいからです。
有界と全有界は,字面だけ見れば全く異なる定義ですね。
有界とは,有限距離に収まっていることを指しています。全有界とは,どんなに小さな円板でも,有限個の円板で覆えることを指します。これを有限被覆 (ゆうげんひふく; finite cover) をもつということがあります。以下の図が分かりやすいでしょう。
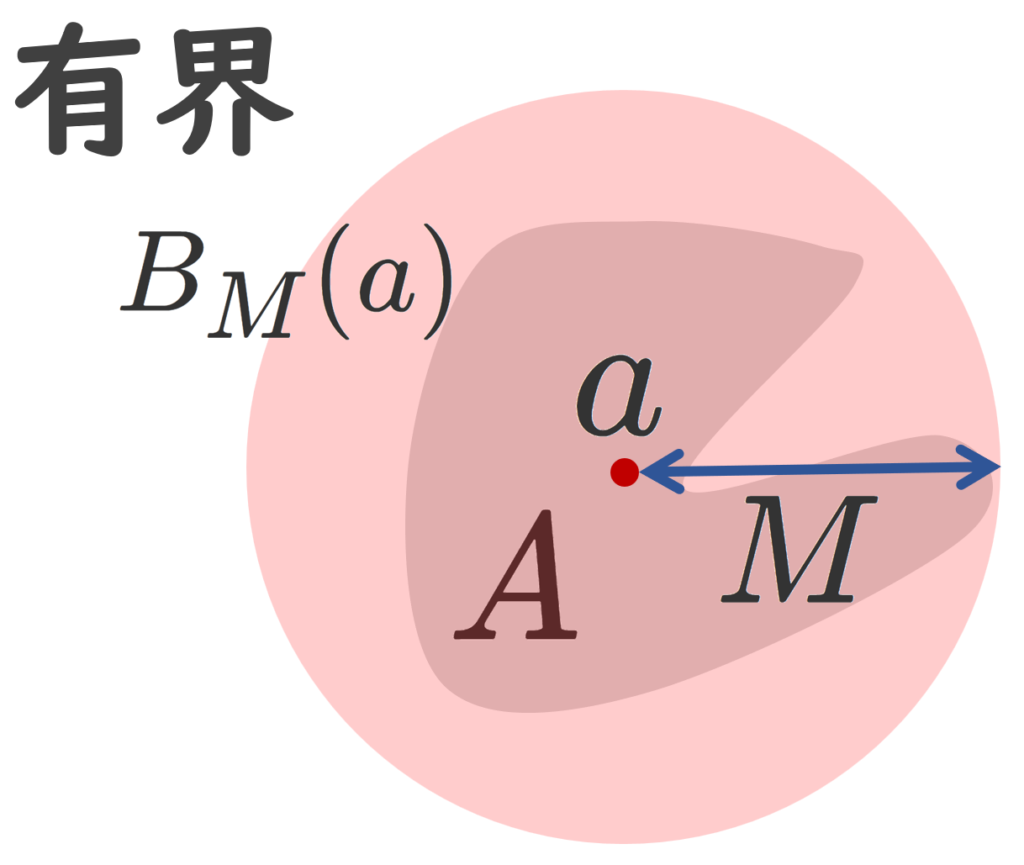
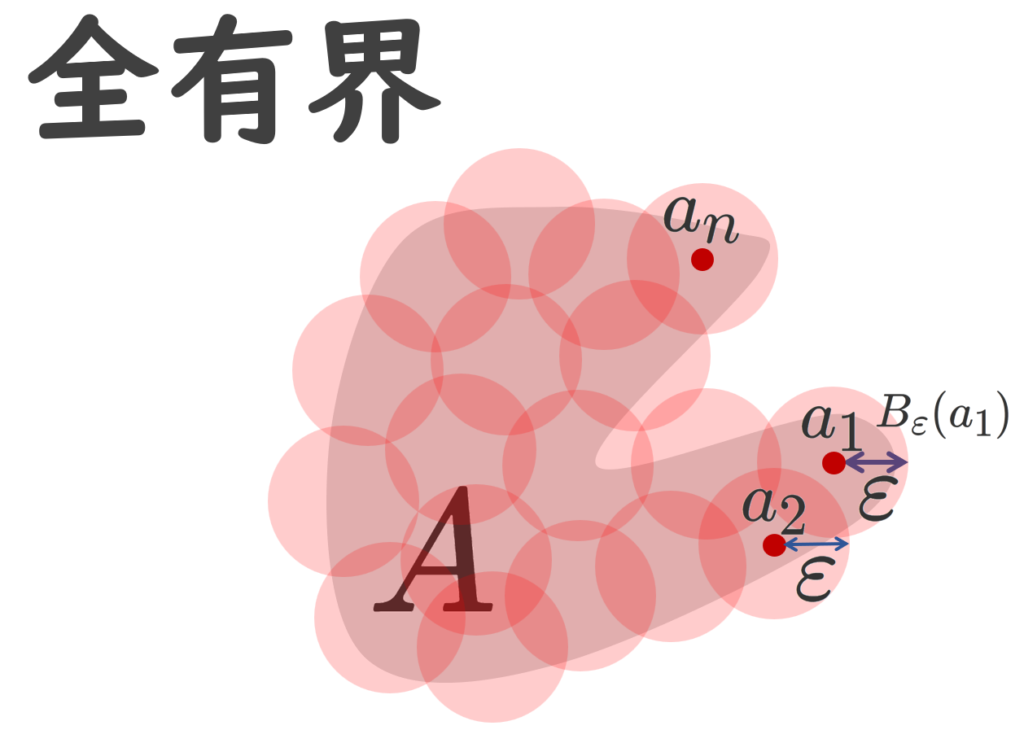
特に全有界は「任意の \varepsilon >0 で」であることが大切です。これを肝に銘じましょう。
全有界ならば有界
具体例を挙げる前に,定理を一つ紹介しましょう。
定理(全有界ならば有界)
(X,d) を距離空間とし, A\subset X とする。 A が全有界であれば,有界である。
証明
\varepsilon >0 とする。 A は全有界であるから, a_1, a_2, \dots, a_n\in A が存在して,A\subset \bigcup_{k=1}^n B_\varepsilon (a_k) とできる。ここで,
M= \max_{2\le k\le n} d(a_1, a_k)
とすると, \bigcup_{k=1}^n B_\varepsilon (a_k) \subset B_{M+\varepsilon}(a_1) となることを示そう。 x\in B_\varepsilon (a_k) とすると,
より, x\in B_{M+\varepsilon}(a_1) が示せた。故に, A\subset B_{M+\varepsilon}(a_1) となるから, A は有界である。
証明終
全有界の例・そうでない例
例1(ユークリッド空間)
d 次元ユークリッド空間 \R^d における部分集合 [-1,1]^d は有界であり,全有界でもある。
\varepsilon>0 に対し, [-1,1]^d\subset B_{\sqrt{d}+\varepsilon}(0) ですから, [-1,1]^d は有界です。
一般に,ユークリッド空間 \R^d における有界集合 A は全有界です。証明しておきましょう。
ユークリッド空間なら有界 ⇒ 全有界の証明
A\subset B_M(0) とすると, B_M(0)\subset [-M,M]^d であるから, [-M, M]^d が全有界であることを示せばよい。ほぼ同じことなので, [0,1]^d が全有界であることを示す。
\varepsilon >0 とする。正の整数 m\ge 1 を十分大きくとることで, 1/m<\varepsilon/\sqrt{d} とできる。各次元の [0,1] 区間を m 分割してできる格子点を
D=\left\{ \left(\frac{k_1}{m}, \dots, \frac{k_d}{m}\right)\middle| 0\le k_1, \dots, k_d\le m\right\}
とすると,[0,1]^d\subset \bigcup_{a\in D}B_\varepsilon(a) となっている。 よって全有界である。
証明終
例2(離散距離)
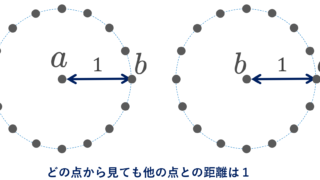
X を無限集合とし, d(x,y)=\begin{cases} 1 & x\ne y, \\ 0 & x=y\end{cases} とすると, (X,d) は距離空間となる(離散距離空間 (discrete metric space) という)。
この空間は有界であるが,全有界ではない。
a\in X に対し, X\subset B_2(a) ですから,有界です。一方で, 0<\varepsilon\le 1 とすると, B_\varepsilon (a)=\{a\} ですから,半径 \varepsilon の有限個の円板で X は覆えません。よって全有界でないです。
離散距離空間は以下でも解説しています。
例3(無限次元空間)
二乗和が収束する実数列空間 \ell^2=\{ \{a_n\}\subset\R\mid \sum_n |a_n|^2 <\infty\} について,
d(\{a_n\}, \{b_n\})=\sqrt{\sum_n |a_n-b_n|^2}
と定めることで, (\ell^2, d) は距離空間と思える(より一般にヒルベルト空間と思える)。このとき,
は有界部分集合であるが,全有界ではない。
全有界でないことは,次のように示せます。
まず, s^{(j)}\in B_1(0) を前から j 番目の数だけ 1/2 で残りの数が 0 であるような数列とします。 i\ne j のとき, d(s^{(i)}, s^{(j)})=1/\sqrt{2} なので, 0<\varepsilon<1/2\sqrt{2} とすれば,どの異なる s^{(j)} も同じ円板 B_\varepsilon (a) に入らないようにできます。
したがって,無限個の s^{(1)}, s^{(2)},\dots を覆うためには,半径 \varepsilon の円板を無限個用意する必要があり, B_1(0) を半径 \varepsilon の有限個の円板で覆うことができないことが分かりますね。
全有界性が重要になる定理
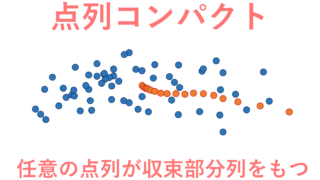
一般に,ユークリッド空間においては有界閉集合あることと,コンパクトであることは同値です(→ボルツァノ–ワイエルシュトラスの定理とその証明)。しかし,距離空間ではそうではありません。距離空間においては,全有界かつ完備であることが,コンパクトであることの必要十分条件です。
全有界はこの辺の話をするときに,初めて出てくる概念かもしれません。この定理は,以下で解説しています。