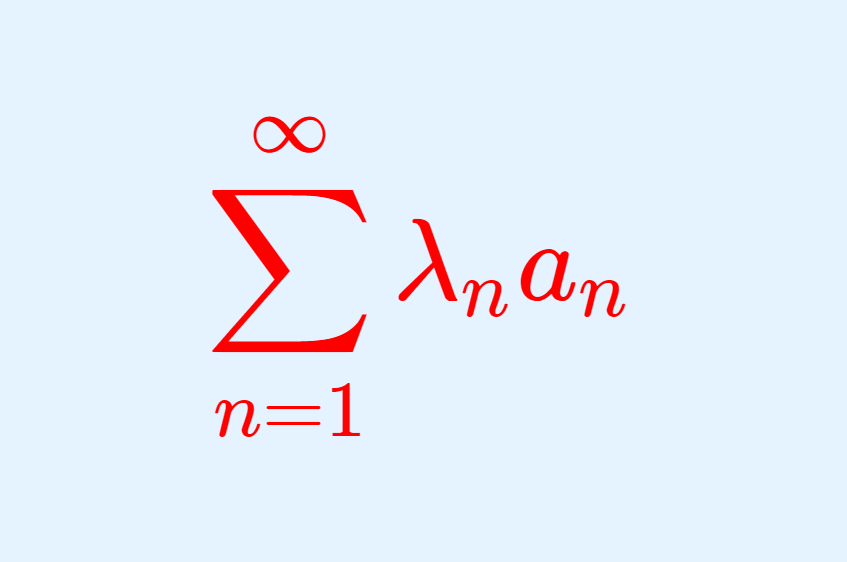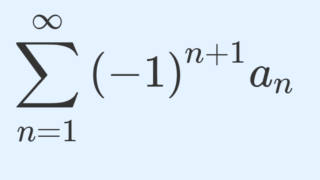「ディリクレの収束判定法」または「ディリクレの定理」といわれる,級数が収束する十分条件を紹介します。そのために必要となる「部分和分」の証明も行います。
ディリクレの定理の主張
定理(ディリクレ; Dirichlet)
実数の数列 \{\lambda_n\} は単調かつ \lambda_n \xrightarrow{n\to\infty} 0 とし,実数または複素数の数列 \{a_n\} は,その部分和列 \{S_n = \sum_{k=1}^n a_k\}_n が有界であるとする。
このとき,
は収束する。
これは,交代級数の収束の定理である「ライプニッツの定理」の一般化だと言えます。実際, a_n = (-1)^{n+1} とすると, \sum_{n=1}^\infty (-1)^{n+1} \lambda_n は収束することが,この定理から分かります。
証明に使う補題~部分和分~
直接証明するのではなく,まずは定理の証明に使う補題を紹介します。(→ 定義・公理・定理・命題・補題・系を完全理解しよう)
補題の主張~部分和分~
補題(部分和分; Summation by parts)
数列 \{a_n\}, \{b_n\} に対し,A_n = \sum_{k=1}^n a_k, B_n = \sum_{k=1}^n b_k とおく。このとき,
\color{red} \sum_{k=1}^n a_n b_n = a_n B_n - \sum_{k=1}^{n-1} (a_{k+1}- a_k) B_k
が成立する。
これは,部分積分 \int fg = fG- \int f' G の離散版だと思えます。証明をしておきましょう。
補題の証明
補題の証明
以下, A_0 = B_0 = 0 と解釈する。 b_{k} = B_{k} - B_{k-1} であるから,
\begin{aligned} \sum_{k=1}^n a_k b_k & = \sum_{k=1}^n a_k (B_{k} - B_{k-1}) \\ &= \sum_{k=1}^n a_k B_k - \sum_{k=1}^{n} a_k B_{k-1} \\ & = \sum_{k=1}^n a_k B_k - \sum_{k=1}^{n-1} a_{k+1} B_{k}. \end{aligned}
一方で,
のため,両辺一致している。
証明終
ディリクレの定理の証明
それでは,定理の証明をしましょう。定理を再掲します。
定理の再掲(ディリクレ; Dirichlet)
実数の数列 \{\lambda_n\} は単調かつ \lambda_n \xrightarrow{n\to\infty} 0 とし,実数または複素数の数列 \{a_n\} はその部分和列 \{S_n = \sum_{k=1}^n a_k\}_n が有界であるとする。
このとき,\color{red} \sum_{n=1}^\infty \lambda_n a_n は収束する。
証明においては, \{a_n\} は単調減少としましょう。単調増加でもほぼ同じです。
証明
\{S_n = \sum_{k=1}^n a_k\} は有界であったから, |S_n| < M, \,\, (n\ge 1) としよう。
部分和分の補題より,
\begin{aligned} &\sum_{k=1}^n \lambda_k a_k \\ &= \lambda_n S_n - \sum_{k=1}^{n-1} (\lambda_{k+1}- \lambda_k) S_k \end{aligned}\tag{1}
である。各項について,
より,第一項は収束し, \lambda_{k+1}- \lambda_k \le 0 に注意して,
であるから,第二項については絶対収束する。
よって, (1) 式の右辺が収束するから,左辺も収束する。
証明終
絶対収束するとは言っていない
証明の中で, \sum_{n=1}^{\infty} (\lambda_{n+1}- \lambda_n) S_n が絶対収束することを示しましたが,元の級数 \sum_{n=1}^\infty \lambda_n a_n が絶対収束するわけではありません。これは,交代級数のライプニッツの定理で,
\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} = \log 2
であるが, \sum_{n=1}^\infty 1/n = \infty であることが反例になります。
基本的な応用
ディリクレの定理を用いれば,たとえば以下のようなことが分かります。
例
\{a_n\} は単調減少かつ a_n \xrightarrow{n\to\infty} 0 とすると,
- \displaystyle \sum_{n=1}^\infty a_n \sin n \theta \, (\theta \in \mathbb{R} ) は収束する。
- \displaystyle \sum_{n=1}^\infty a_n \cos n \theta \, (\theta \in \mathbb{R}\setminus \{2m\pi\mid m \in \mathbb{Z}\}) は収束する。
- \displaystyle \sum_{n=1}^\infty a_n e^{in\theta} \, (\theta \in \mathbb{R}\setminus \{2m\pi\mid m \in \mathbb{Z}\}) は収束する。