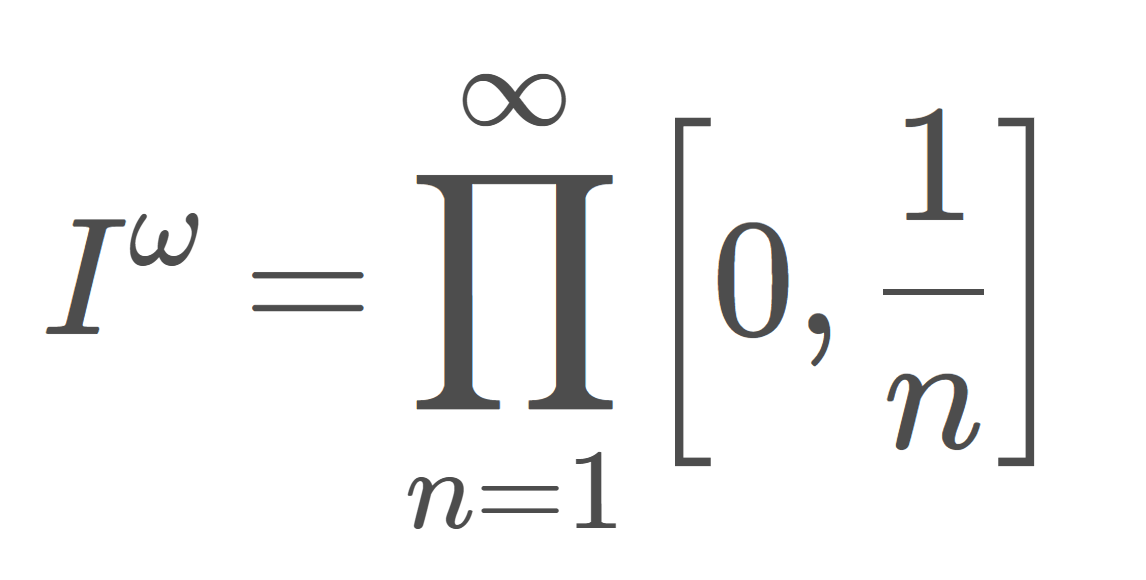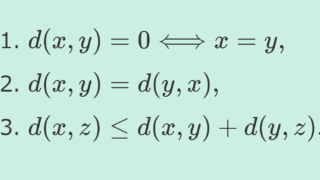ヒルベルト立方体とは,閉区間の可算個の直積で定義される位相空間で,距離化可能な空間,2乗可積分な数列のなすヒルベルト空間の部分集合です。ヒルベルト立方体について,その定義と位相的性質を解説しましょう。
ヒルベルト立方体の定義
定義(ヒルベルト立方体)
n\ge 1 に対し,通常の位相が入った閉区間 [0,1/n] の直積位相空間
\color{red}\Large I^\omega = \prod_{n=1}^\infty \left[ 0,\frac{1}{n}\right]
をヒルベルト立方体 (Hilbert cube) という。
\prod_{n=1}^\infty \left[ 0,1/n\right] とは, 0\le a_n\le 1/n となる数列 (a_n) 全体の集合を指します。すなわち,
\prod_{n=1}^\infty \left[ 0,\frac{1}{n}\right]=\left\{ (a_n)\middle| 0\le a_n\le \frac{1}{n}\right\}
です。各区間で, [0, 1/n]\cong [0,1] ( \congは同相の意味)なので,
が成り立ちます。右辺は [0,1]^\mathbb{N} や [0,1]^\omega とかくので,それに乗じて本記事では,ヒルベルト立方体を I^\omega とかくことにします。
ヒルベルト立方体の性質

ヒルベルト立方体は,距離化可能な位相空間です。
定理(ヒルベルト立方体は距離化可能)
x=(x_n), y=(y_n)\in I^\omega に対し,
d(x,y) =\left( \sum_{n=1}^\infty |x_n-y_n|^2\right)^{1/2}\ell^2 を, \sum_{n=1}^\infty |a_n|^2<\infty をみたす実数列全体の集合とすると, これは関数解析で頻出のヒルベルト空間です。今は, I^\omega \subset \ell^2 であり, I^\omega は \ell^2 の部分距離空間と思えます(部分ベクトル空間ではない)。
距離化可能なので,距離空間で成り立つ性質は成り立ちます。
ヒルベルト立方体と可算公理
距離空間においては,第二可算 \iff 可分です(→第二可算公理と第二可算な位相空間の例・性質)。
可分であることは, I^\omega における,有限個のみ 0 でない有理数列全体の集合が可算集合かつ I^\omega 上稠密であることから分かります。
ヒルベルト立方体と分離公理
| T_0, T_1, T_2 | T_3 | T_4, T_5 |
|---|---|---|
| 〇 | 〇 | 〇 |
本記事では, T_0 から T_5 は以下のように定義しています。この定義は文献によって変わりますから,注意してください。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ空間 (Kolmogorov space) | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_1 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ空間 (Hausdorff space) | 任意の異なる2点 x,y\in X に対して, x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F に対して, F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| T_4 | 任意の2つの互いに素な空でない閉集合 F,G\subset X に対して, F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| T_5 | \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの空でない集合 A,B\subset X に対して, A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset となる開集合 O_A, O_B が取れる |
距離空間であれば, T_0 から T_5 のすべての分離公理が成り立ちます。距離空間は完全正規空間 (completely normal T_1 かつ T_5) だし,正則空間 ( T_0 かつ T_3)ともいえます。
ヒルベルト立方体とコンパクト性
各 [0,1/n] がコンパクトであることと,「コンパクト空間の直積はコンパクトである」というチコノフの定理 (Tychonoff’s theorem) により, I^\omega はコンパクトです。
距離空間においては,コンパクトと点列コンパクトは同値なので,点列コンパクトにもなります。
ヒルベルト立方体と連結性
| 連結 | 弧状連結 | 弧連結 | hyperconnected | ultraconnected |
|---|---|---|---|---|
| 〇 | 〇 | 〇 | × | × |
各定義は以下の通りです。
| 名称 | 定義 |
|---|---|
| 連結 (connected) | 2つの互いに素な開集合 U,V で, U\cup V=X となっているものは存在しない |
| 弧状連結 (path connected) | 任意の異なる2点 x,y\in X について,ある連続写像 f\colon [0,1]\to X で, f(0)=x, f(1)=y となるものが存在する |
| 弧連結 (arc connected) | 上の f として,埋め込みすなわち f\colon [0,1]\to f([0,1]) が同相となっているものが常に取れる(※[1]では単に全単射なものが取れるとしている。 X がハウスドルフ ( T_2)なら弧状連結と弧連結は同値) |
| hyperconnected | 任意の空でない2つの開集合が常に共通部分を持つ |
| ultraconnected | 任意の空でない2つの閉集合が常に共通部分を持つ |
定義から明らかに弧連結 \implies 弧状連結だし,また一般に弧状連結 \implies 連結なので,弧連結であることを示しましょう。
弧連結であることの証明
x=(x_n), y=(y_n)\in I^\omega に対し, f\colon [0,1]\to I^\omega を
f(t) = (1-t)x+ty=\bigl( (1-t)x_n+ty_n\bigr)
と定義すれば f \colon [0,1]\to f([0,1]) は同相である。
証明終
また,hyperconnected でないことは, (0,1/2)\times [0,1]^\mathbb{N}\cap (1/2,1)\times [0,1]^\mathbb{N}=\emptyset であることからすぐわかりますし,ultraconnected でないことは,1点集合が閉集合であるからです。