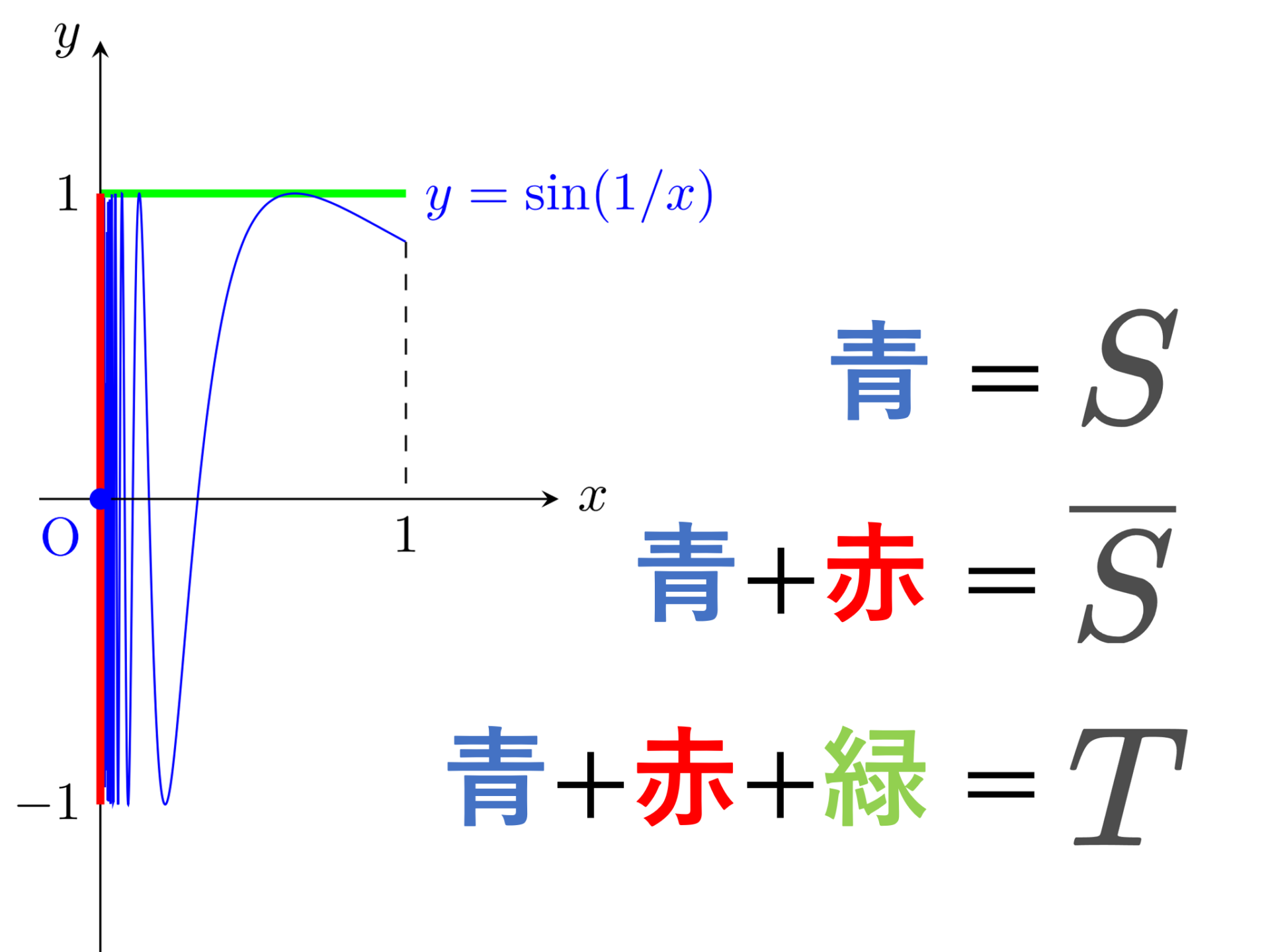
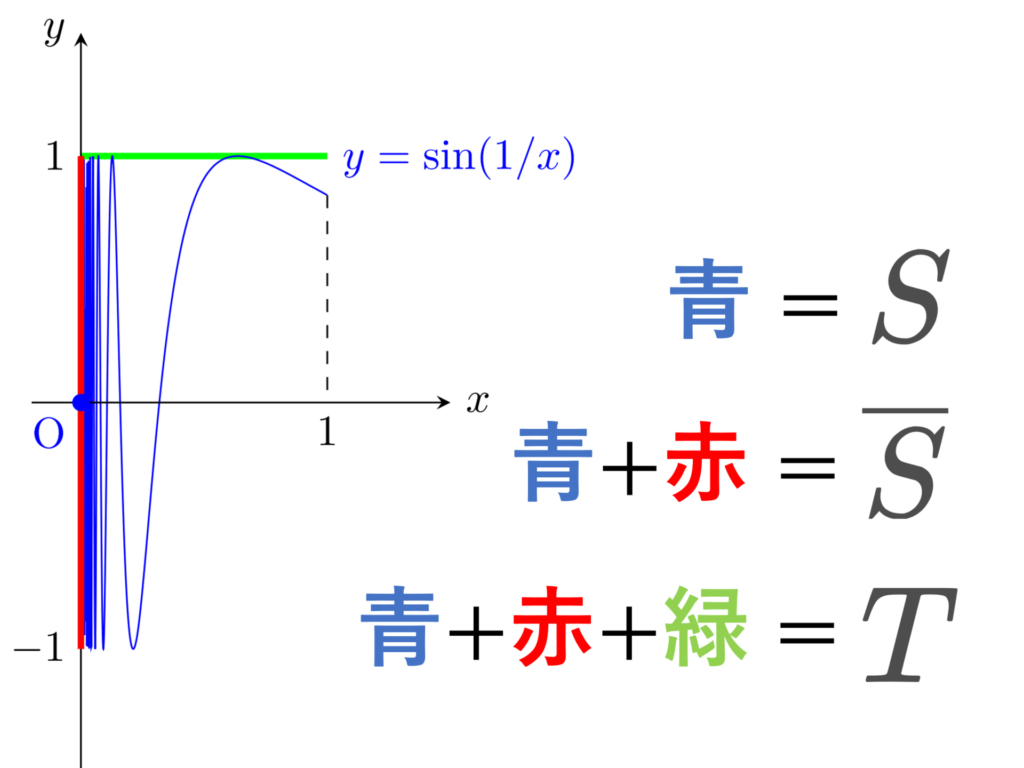
位相幾何学者の正弦曲線，あるいは英語でTopologist’s sine curveと呼ばれる曲線は， xy 平面における曲線 y=\sin (1/x)\;(0<x\le 1) に原点を付加した図形です。
連結だが弧状連結でない・局所連結でないものとして有名です。位相幾何学者の正弦曲線について考えましょう。
位相幾何学者の正弦曲線
定義（位相幾何学者の正弦曲線）
\R^2 の部分集合
\color{red} S=\left\{\left(x, \sin\frac{1}{x}\right)\middle| 0<x\le 1\right\}\cup \{(0,0)\}
に， \R^2 から定まる相対位相を入れた部分位相空間 S を位相幾何学者の正弦曲線 (Topologist’s sine curve) という。
また， S の \R^2 における閉包
\Large \color{red} \overline{S} = S\cup \left(\{0\}\times [-1,1]\right)
を閉じた位相幾何学者の正弦曲線 (closed Topologist’s sine curve) という。
さらに，
\Large \color{red} T=\overline{S}\cup \left([0,1]\times \{1\}\right)
を拡張された位相幾何学者の正弦曲線 (extended Topologist’s sine curve) という。
以下の図が分かりやすいでしょう。
位相幾何学者の正弦曲線の位相的性質
まずは紹介する性質をまとめましょう。
| S | \overline{S} | T | |
|---|---|---|---|
| 第一可算・第二可算・可分 | 〇 | 〇 | 〇 |
| 距離化可能 | 〇 | 〇 | 〇 |
| T_0, T_1,T_2, T_3, T_4, T_5 空間 | 〇 | 〇 | 〇 |
| コンパクト・点列コンパクト・局所コンパクト | × | 〇 | 〇 |
| 連結 | 〇 | 〇 | 〇 |
| 弧状連結・弧連結 | × | × | 〇 |
| 局所連結 | × | × | × |
順番に考えます。
1. 第一可算・第二可算・可分であること
第二可算の部分空間は第二可算だし，第二可算なら第一可算なので，第一可算・第二可算は明らかです。
また S_\mathbb{Q} = \left\{\left(q, \sin(1/q)\right)\mid 0<q\le 1,\, q\in\mathbb{Q} \right\} は稠密な可算集合なので， S,\overline{S} は可分だし，また， T も明らかに可分です。
可分であることは，第二可算であることと，距離空間において可分性と第二可算性は同値であることからも従います。
2. 距離化可能であること・T0からT5空間までの全てをみたすこと
S, \overline{S},T\subset \R^2 であるから， \R^2 の距離によってこれら3つの部分空間は距離化可能です。
距離空間は， T_0 から T_5 まで全てみたすので，示せました。
3. コンパクト性について
| S | \overline{S} | T | |
|---|---|---|---|
| コンパクト・点列コンパクト・局所コンパクト | × | 〇 | 〇 |
S=\left\{\left(x, \sin(1/x)\right)\middle| 0<x\le 1\right\}\cup \{(0,0)\} ですから，通常の y=\sin x が x\to\pm\infty まで永遠に波打っているのに対し， S は有界な正方形 [0,1]\times [-1,1]\subset \R^2 の中に収まっていることに注意してください。
コンパクト性について本サイトでは，以下の定義を採用しています。
| 名称 | 定義 |
|---|---|
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
距離空間においては，コンパクト性と点列コンパクト性は同値です。以下で， \varepsilon>0 に対し，点 p=(a,b)\in P\subset \R^2 の集合 P における \varepsilon-近傍を
B_\varepsilon^P(p) = \{ (x,y)\in P\mid (x-a)^2+(y-b)^2<\varepsilon^2\}
とします。
証明
S について
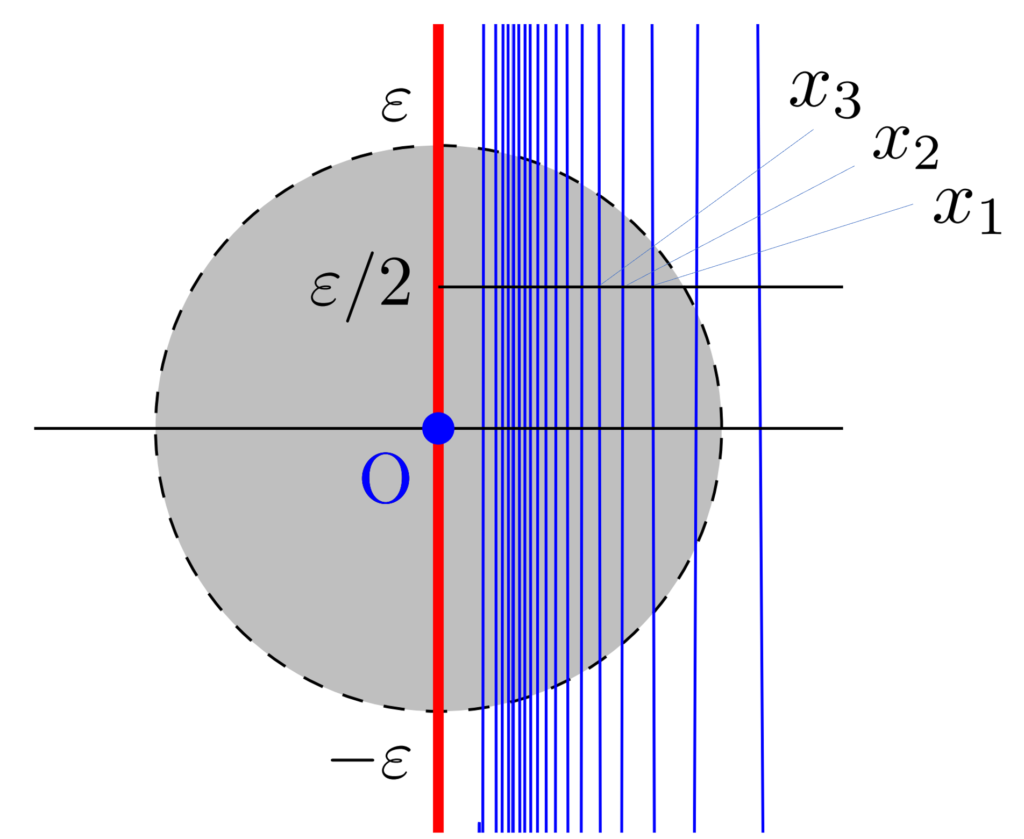
0=(0,0)\in S の任意の近傍 N がコンパクトでないこと，すなわち点列コンパクトでないことを示す。ある \varepsilon >0 に対し，
0\in B_\varepsilon^S(0)\subset N
とできる。このとき，直線 y=\varepsilon/2 と B_\varepsilon^S(0) の交点のうち， x 座標が大きい順に x_1, x_2, x_3,\ldots とすると， x_n\to (0,\varepsilon/2)\notin N となるので， N が点列コンパクトでないことが示された。
\overline{S}, T について
\overline{S}, T はどちらも \R^2 における有界閉集合であるから，コンパクトである。
証明終
4. 連結性について
| S | \overline{S} | T | |
|---|---|---|---|
| 連結 | 〇 | 〇 | 〇 |
| 弧状連結・弧連結 | × | × | 〇 |
| 局所連結 | × | × | × |
連結にまつわる定義は以下の通りです。 S は連結だが弧状連結でない・局所連結でない例として， T は連結・弧状連結だが局所連結でない例としてよく使われます。
| 名称 | 定義 |
|---|---|
| 連結 (connected) | 2つの互いに素な開集合 U,V で， U\cup V=X となっているものは存在しない |
| 弧状連結 (path connected) | 任意の異なる2点 x,y\in X について，ある連続写像 f\colon [0,1]\to X で， f(0)=x, f(1)=y となるものが存在する |
| 弧連結 (arc connected) | 上の f として，埋め込みすなわち f\colon [0,1]\to f([0,1]) が同相となっているものが常に取れる（※単に全単射なものが取れるとすることもある。 X がハウスドルフ ( T_2)なら弧状連結と弧連結は同値） |
| 局所連結 (locally connected) | 各点で連結な基本近傍系をもつ |
証明
連結であることについて
f(x)=(x, \sin (1/x)) とすると， f\colon (0,1]\to S は連続であり， f((0,1])=S\setminus \{(0,0)\} であるので，右辺は連結である。
S\setminus \{(0,0)\} \subset S\subset \overline{S\setminus \{(0,0)\}} = \overline{S}
であるから， S や \overline{S} も連結である。また，
であり，[0,1]\times \{1\} は連結かつ S と共通部分をもつから， T も連結である。
局所連結でないことについて
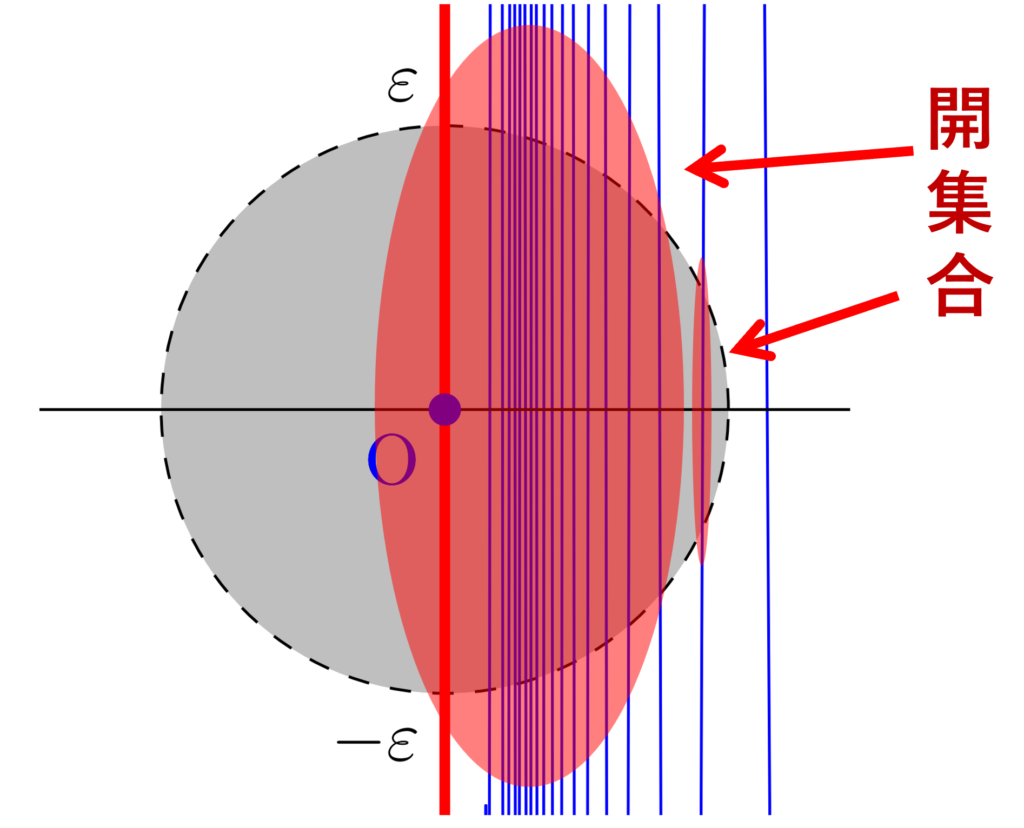
0<\varepsilon <1/2 とする。0= (0,0) の S, \overline{S}, T における \varepsilon-近傍 B_\varepsilon^S(0),B_\varepsilon^{\overline{S}}(0),B_\varepsilon^T(0) はどれも明らかに連結でない。下図のようなイメージである。よって，局所連結でない。
S, \overline{S} が弧状連結でないことについて
任意の -1\le a\le 1 に対し， S_a=S\cup \{(a,0)\} が弧状連結でないことを示せばよい。任意の -1\le a\le 1 に対し， (a,0) と (1, \sin 1) を結ぶ道がないことを示す。もし道があったとすると，ある連続な F\colon [0,1]\to S_a で， F(0)=(0, a),\, F(1)=(1, \sin 1) となるものが存在する。
自然な射影 p_1 \colon (x,y)\mapsto x を考えると， p_1\circ F は連続なので，連結な集合 [0,1] の像 p_1\circ F([0,1]) も連結であることと，0,1\in p_1\circ F([0,1]) であることより，中間値の定理を帰納的に使うことで，
p_1\circ F(t_n)=\frac{1}{(n-1/2)\pi},\quad n\ge 1
となる 1>t_1>t_2>t_3>\cdots > 0 が取れる。有界な単調減少列は収束するので， t_n\xrightarrow{n\to\infty} t とすると， p_1\circ F の連続性より， p_1\circ F(t)=0 である。よって， F(t)=(0,a) でなければならないが，
で n\to \infty としても (0,a) には収束しない。これは F の連続性に矛盾する。
T が弧状連結であることについて
上の証明より，明らかに \overline{S} の弧状連結成分は \{0\}\times [-1,1] と \{(x, \sin(1/x)\mid 0<x\le 1\} の2つである。 T はこの2つが \{1\}\times [0,1] によってつながるから，弧状連結である。
証明終
本例は，連結集合の閉包は常に連結ですが，弧状連結集合の閉包は弧状連結とはいえない例にもなっています。
