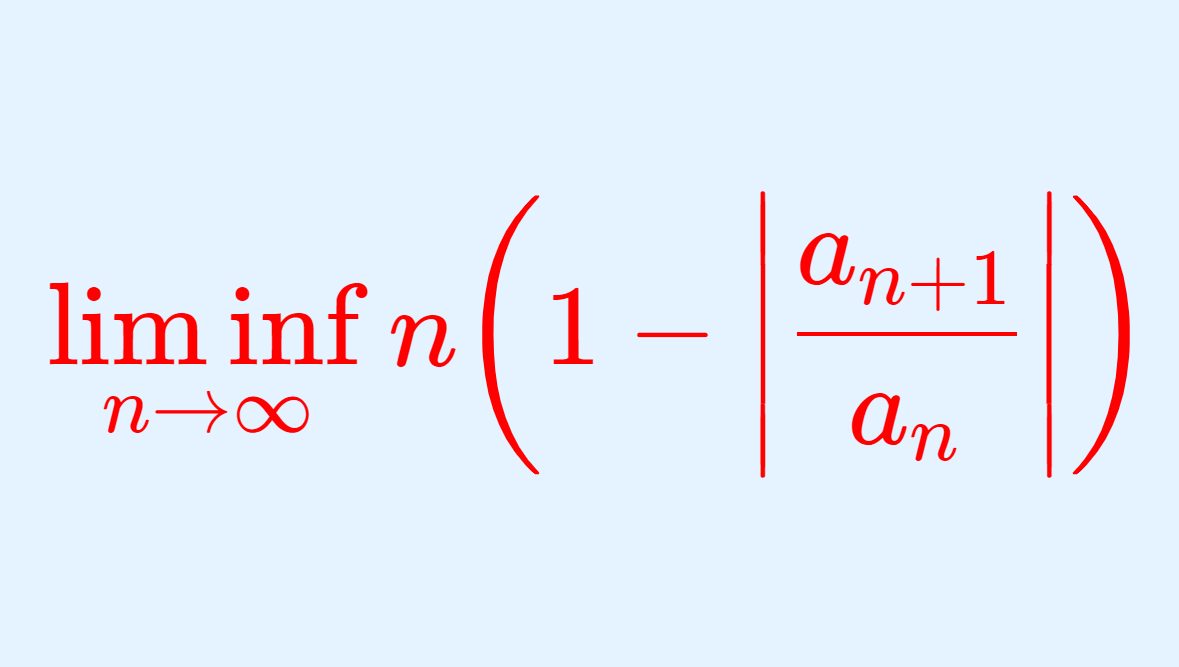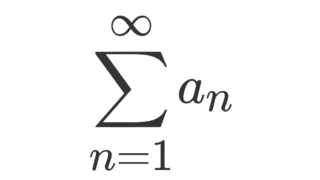級数の収束判定法で最も有名なものと言えば,ダランベールの収束判定法でしょう。しかしながら,これは
\lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right| = 1
のとき,収束・発散の判定ができないという問題があります。これを克服しようとする一つの方法が,ラーベの収束判定法 (Raabe’s test) です。これを紹介しましょう。
ラーベの収束判定法
定理(ラーベの収束判定法; Raabe’s test)
数列 \{a_n\} に対し,級数 \sum_{n=1}^\infty a_n の収束・発散について,
\color{red}\liminf_{n\to\infty} n \! \left(1- \left|\frac{a_{n+1}}{a_n}\right|\right ) > 1ならば絶対収束し,
\color{red}\limsup_{n\to\infty} n \! \left(1- \left|\frac{a_{n+1}}{a_n}\right|\right ) < 1
ならば条件収束または発散する(正項級数 a_n > 0 ならば常に発散する)。
\lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right| = 1 という状況において,それを n 倍して収束値を見積もることで,収束を判断しようというわけです。
ダランベールの収束判定法は等比級数 \sum 1/r^n に帰着させますが,ラーベの収束判定法は \sum 1/n^p に帰着させることが知られています。
また,ラーベの判定法は,
\color{red} \liminf_{n\to\infty} n \! \left(\left|\frac{a_{n}}{a_{n+1}}\right|-1 \right ) > 1
ならば収束し,
ならば条件収束または発散する,と言い換えることもできます。
ラーベの収束判定法の具体例
具体例を挙げましょう。「適用できる例」と「適用できない例」をそれぞれ考えます。
ラーベの収束判定法が適用できる例
まずは,ラーベの収束判定法が適用できる例です。
絶対収束する例
例1.
\color{red} a_n = 1/n^2 とする。このとき,
\begin{aligned}n \! \left(1- \left|\frac{a_{n+1}} {a_n}\right|\right) &= n \! \left(1- \left(\frac{n}{n+1}\right)^2\right) \\ &= \frac{n(2n+1)}{(n+1)^2}\xrightarrow{n\to\infty} 2>1\end{aligned}
であるから,\displaystyle \sum_{n=1}^\infty \frac{1}{n^2} は絶対収束する。
ダランベールの収束判定法は使えないことに注意しましょう。
なお, \sum 1/n^p の収束・発散については,【級数】広義積分による収束判定法と1/n^pの和の収束・発散も参照してください。
条件収束または発散する例
例2.
\color{red} a_n = 1/\sqrt{n} とする。このとき,
\begin{aligned}n \! \left(1- \left|\frac{a_{n+1}} {a_n}\right|\right) &= n \! \left(1- \sqrt{\frac{n}{n+1}}\right) \\ &= \frac{n(\sqrt{n+1}-\sqrt{n})}{\sqrt{n+1}} \\ &= \frac{n}{ \sqrt{n+1} (\sqrt{n+1}+\sqrt{n}) }\\ &\xrightarrow{n\to\infty} \frac{1}{2}<1\end{aligned}
であるから,\displaystyle \sum_{n=1}^\infty \frac{1}{\sqrt{n}} は絶対収束しない。特に,いまは正項級数であるから,発散する。
一方で, \color{red} a_n = (-1)^{n-1}/\sqrt{n} とする。上の計算により,同様に絶対収束しないことが分かる。このとき, \displaystyle \sum_{n=1}^\infty \frac{(-1)^{n-1}}{\sqrt{n}} は交代級数の収束性の証明とその具体例により,条件収束する。
これも,ダランベールの収束判定法は使えないことに注意しましょう。
ラーベの収束判定法が適用できない例
つづいて,ラーベの収束判定法が適用できない例を考えましょう。
絶対収束する例
例3.
\color{red} a_n = 1/n(\log n)^2 とする。このとき,
\small \begin{aligned} & n \! \left(1- \left|\frac{a_{n+1}} {a_n}\right|\right) \\ &= n\left\{ 1-\frac{n(\log n)^2}{(n+1)(\log (n+1))^2}\right\} \\ &= \frac{n}{n+1} + \frac{n(\log(n+1)+\log n) \log \left(1+\frac{1}{n}\right)^n}{(n+1)(\log(n+1))^2} \\ &\xrightarrow{n\to\infty} 1 + 0 = 1 \end{aligned}
となるから,ラーベの収束判定法は適用できないが,1/nlogn型の級数の収束・発散により, \displaystyle \sum_{n=2}^\infty \frac{1}{n(\log n)^2} は絶対収束することが知られている。
条件収束する例
例4.
\color{red} a_n = (-1)^{n-1}/n とする。このとき,
\begin{aligned} n \! \left(1- \left|\frac{a_{n+1}} {a_n}\right|\right) &= n\left(1-\frac{n}{n+1}\right) \\ &= \frac{n}{n+1}\xrightarrow{n\to\infty} 1\end{aligned}
であるから,ラーベの収束判定法は適用できないが,交代級数の収束性の証明とその具体例により, \displaystyle \sum_{n=1}^\infty \frac{(-1)^{n-1}}{n} は条件収束することが知られている。
発散する例
例5.
\color{red} a_n = 1/(n\log n) とする。このとき,
\begin{aligned}&n \! \left(1- \left|\frac{a_{n+1}} {a_n}\right|\right)\\ &= n\left(1-\frac{n\log n}{(n+1)\log(n+1)}\right) \\ &=\frac{n}{n+1}+ \frac{n\log\left(1+\frac{1}{n}\right)^n}{(n+1)\log(n+1)}\\ &\xrightarrow{n\to\infty} 1+0 = 1 \end{aligned}
となるから,ラーベの収束判定法は適用できないが,1/nlogn型の級数の収束・発散により, \displaystyle \sum_{n=2}^\infty \frac{1}{n\log n} は発散することが知られている。
ラーベの収束判定法の証明
- 絶対収束する証明
- 発散する証明
のそれぞれの証明を行いましょう。
絶対収束する証明
証明
K = \liminf_{n\to\infty} n \! \left(1- \left|\frac{a_{n+1}}{a_n}\right|\right ) > 1
とし, 1<\alpha < K を一つ定める(たとえば \alpha = (K+1)/2 とすればよい)。このとき,ある N_0\ge 1 が存在して, n\ge N_0 ならば
が成立する。これを式変形すると,
よって,両辺 \sum_{n=N_0}^N とすると,
N\to\infty とすると,
であるから,もとの級数は絶対収束する。
証明終
なお,Wikipedia には,別の証明が載っています。
発散する証明
つづいて,発散する証明もしましょう。
証明
K = \limsup_{n\to\infty} n \! \left(1- \left|\frac{a_{n+1}}{a_n}\right|\right ) < 1
とし, K<\alpha< 1 を取る(たとえば \alpha = (K+1)/2 とすればよい)。このとき,ある N_0\ge 1 が存在して, n\ge N_0 ならば,
が成立する。 したがって, n\ge N_0 ならば,
すなわち, n|a_{n+1}|> (n-1)|a_n| であるから,\{ (n-1)|a_n|\}_{n=N_0}^\infty は狭義単調増加である。よって,ある M >0 が存在して, n|a_{n+1}| \ge M \; (n \ge N_0) とできる。したがって,
である。よって,元の級数は絶対収束しないので,条件収束または発散する。
証明終