連結成分と完全不連結性について～定義と具体例～

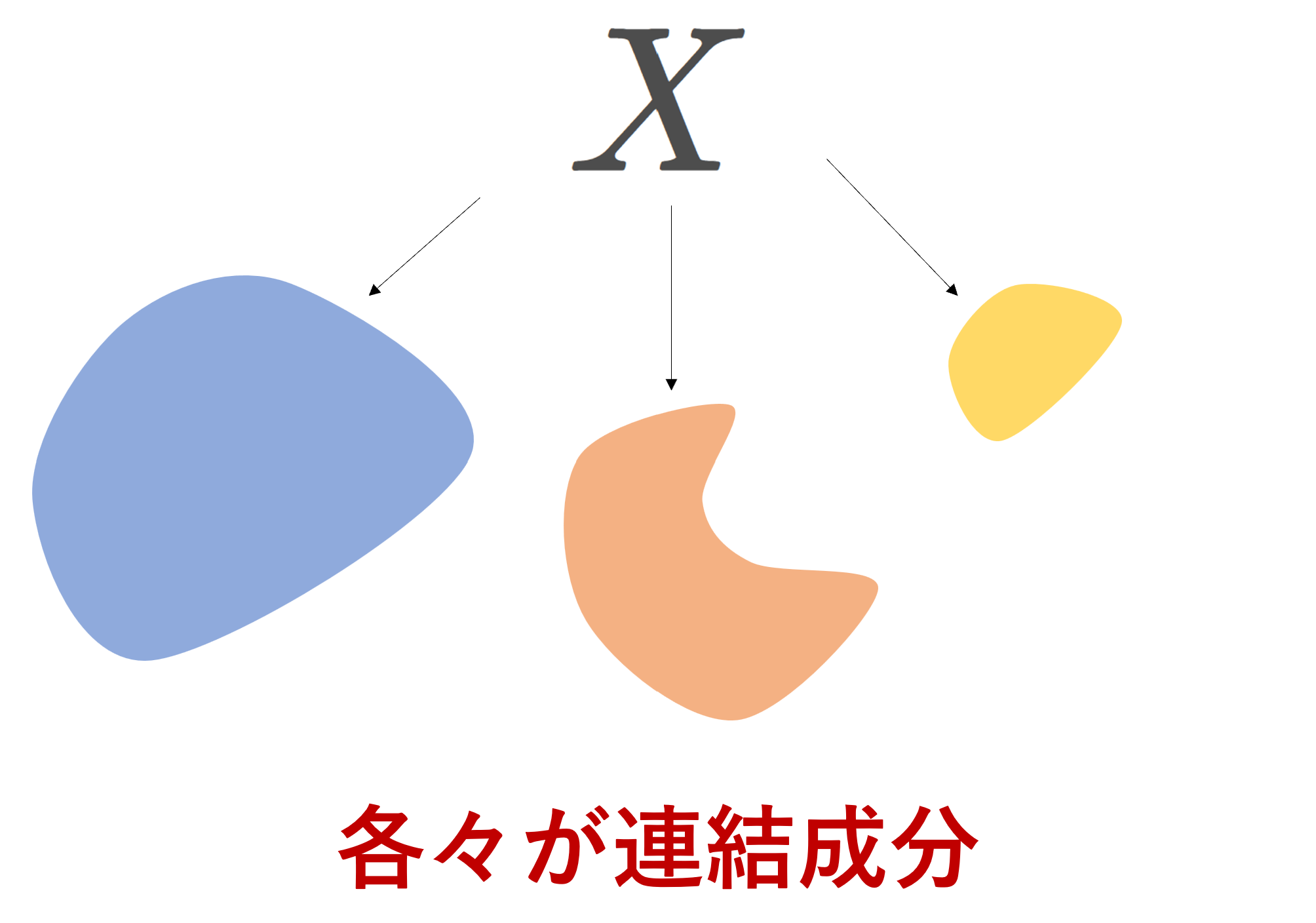
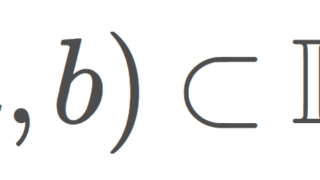位相空間のある点における連結成分とは，その点を含む最大の連結部分集合のことをいいます。また，任意の点の連結成分が自分自身のみの1点集合であるとき，その位相空間は完全不連結であるといいます。

連結成分と完全不連結性について，詳しく紹介しましょう。

連結成分の定義と具体例
1. 連結成分の定義
2. 連結成分の具体例
完全不連結の定義と具体例
連結性に関する概念
関連する記事
参考

連結成分の定義と具体例

位相空間 $(X,\mathcal{O})$ において， $A\subset X$ が連結集合 (connected set) であるとは，部分空間として $A$ が互いに素な（互いに共通部分をもたない）空でない2つの開集合で分離できないことをいいます。詳しくは以下を参照してください。本記事では，連結性の定義は既知とします。

これをもとに，連結成分について定義していきましょう。

連結成分の定義

定義1（連結成分）

$(X,\mathcal{O})$ を位相空間とし， $x\in X$ とする。

$x$ を含む最大の連結集合を(本記事では) $\Large\color{red} C_x$ とかき，これを $x$ の連結成分 (component) という。

一般に $A\subset X$ が連結であるとき，その閉包 $\overline{A}$ も連結であるから，連結成分は常に閉集合である。

$\mathcal{C}_x= \{ C\subset X \mid x\in C\text{ and }C\text{ is connected}\}$ を， $x$ を含む連結集合全体の集合としましょう。 $\{x\}\in\mathcal{C}_x$ なので， $\mathcal{C}_x$ は空ではありません。ここで， $x\in \bigcap_{C\in\mathcal{C}_x} C$ であることから，

C_x = \bigcup_{C\in\mathcal{C}_x} C

も連結集合であり(→位相空間における連結性について詳しく)， $C_x\in \mathcal{C}_x$ です。これが $x$ を含む最大の連結集合になっているわけです。

$x,y\in X$ に対し， $C_x=C_y$ または $C_x\cap C_y=\emptyset$ のいずれかが必ず成立します。実際，もし $C_x\cap C_y\ne\emptyset$ だとすると， $C_x\cup C_y$ も連結になります。 $C_x, C_y$ はそれぞれ $x,y$ を含む最大の連結集合ですから， $C_x=C_y=C_x\cup C_y$ になりますね。

$C_x=C_y$ のとき， $x\sim y$ と定義すると， $\sim$ は同値関係になっているとも言えます。連結成分の概念は， $X$ を同値関係による同値類で分類しているという風にも捉えられます。

連結成分の具体例

連結成分の具体例1(連結空間).

位相空間 $(X,\mathcal{O})$ が連結であるとき，任意の $x\in X$ に対し， $C_x=X$ である。

$X$ が連結であるときは，任意の点における最大の連結集合は $X$ そのものです。

連結成分の具体例2( $\R$ の部分集合).

$\R$ の部分集合 $X= [0,1]\cup (2,3) \cup \{4\}$ において，

C_x=\begin{cases} [0,1] & 0\le x\le 1 ,\\ (2,3) & 2<x<3, \\ \{4\} & x=4 \end{cases}

である。

連結成分の概念によって， $X$ を3つの互いに素な連結集合 $[0,1], (2,3), \{4\}$ に分割しているわけです。

完全不連結の定義と具体例

任意の点の連結成分が1点集合であるとき，完全不連結といいます。

完全不連結の定義

定義2（完全不連結）

$(X,\mathcal{O})$ を位相空間とする。任意の $x\in X$ に対し， $C_x=\{x\}$ となるとき， $X$ を完全不連結 (totally disconnected) という。

具体例を挙げましょう。

完全不連結な空間の具体例

完全不連結な例1(離散空間).

$(X,2^X)$ を離散空間とするとき，この空間は完全不連結である。

離散空間においては，2点以上の部分集合は連結になりませんので，任意の点 $x\in X$ で $C_x=\{x\}$ となります

完全不連結な例2( $\mathbb{Q}$ ).

有理数全体の集合 $\mathbb{Q}$ は完全不連結である。

$\mathbb{Q}$ に入っている位相は離散位相ではありません。たとえば1点集合は開集合ではありません。完全不連結は「点同士が離れている」イメージを持っているかもしれませんが，離散的ではありません。注意してください。

$A\subset \R$ が連結で， $x,y\in A, \, x<y$ ならば， $[x,y]\subset A$ でなければなりません。もし， $x<z<y$ が $z\notin A$ ならば， $A\cap (-\infty,z), A\cap (z,\infty)$ のように， $A$ を2つの互いに共通部分をもたない開集合で分離できてしまうからです。次の例も同様です。

完全不連結な例3(カントール集合).

カントールの3進集合は完全不連結である。

直前の， $\mathbb{Q}$ が完全不連結であることの説明とほぼ同じ理由です。

完全不連結な例4(ゾルゲンフライ直線).

\mathcal{B}_l=\{ [a,b)\subset \R\mid a<b\}

を開基とする位相 $\mathcal{O}_l$ を下限位相 (lower limit topology, right half-open interval topology) といい，位相空間 $(\R, \mathcal{O}_l)$ をゾルゲンフライ直線 (Sorgenfrey line) という。ゾルゲンフライ直線は完全不連結である。

$(-\infty, a)=\bigcup_{n=1}^\infty [a-n, a)$ と $[a,\infty)= \bigcup_{n=1}^\infty [a, a+n)$ なので，ゾルゲンフライ直線においては， $(-\infty, a), [a,\infty)$ も開集合です。

完全不連結であることを示しましょう。 $A\subset \R$ が2点以上の集合だとすると，ある $a\in A$ が存在して，

A\cap (-\infty, a) ,\quad A\cap [a,\infty)

がともに空でない集合にできます。どちらの集合も $A$ における相対位相において開集合ですから， $A$ は連結ではありませんね。よって完全不連結であることが示せました。

ゾルゲンフライ直線については，以下の記事でも掘り下げています。

任意の点がその位相に関して開かつ閉な近傍からなる基本近傍系をもつ位相空間を0次元 (zero-dimensional) ということがあります。ゾルゲンフライ直線は，開かつ閉である開基をもつので，0次元です。というか，完全不連結な例1.から例4.まで全て0次元です。

一般に，0次元な $T_1$ 空間は完全不連結です。なぜなら， $X$ が0次元な $T_1$ 空間とし， $x\in A\subset X$ かつ $A$ を2点以上の集合， $y\in A\setminus \{x\}$ としたとき，ある開かつ閉な近傍 $x\in U\subset X$ で， $y\notin U$ となるものが取ってこれますが， $x\in U\cap A\subsetneq A$ が $A$ における開かつ閉な部分集合となるため， $A$ は連結ではないからです。

なお，0次元だけでは完全不連結とは限りません。たとえば密着空間は0次元ですが，連結です。

完全不連結な空間の性質

定理（完全不連結な空間の性質）

完全不連結な空間は $T_1$ 空間である
完全不連結な空間の部分空間は完全不連結である
完全不連結な空間の直積は完全不連結である

$T_1$ 空間であることは，任意の1点集合が閉集合であることと同値です(→【位相空間】T1空間の定義・具体例と性質)。定義1で述べた通り，連結成分は常に閉集合ですから，完全不連結な空間では，1点集合は閉です。よって，1.が示せました。

2.は明らかなので，3.を証明しましょう。

3.の証明

$(X_\lambda)_{\lambda\in \Lambda}$ を完全不連結な空間の族とし， $X=\prod_{\lambda\in \Lambda} X_\lambda$ を考える。

$A\subset X$ を連結な部分集合とする。このとき，射影 $p_\lambda\colon X\to X_\lambda$ の連続性により， $p_\lambda(A)\subset X_\lambda$ は連結である。 $X_\lambda$ は完全不連結なので， $p_\lambda(A)$ は1点集合である。ゆえに， $A$ は1点集合である。

したがって， $X$ は完全不連結である。

証明終

なお，連結集合の連続像は連結ですが，完全不連結な集合の連続像が完全不連結とは限りません。たとえば，2点以上の点をもつ完全不連結空間から，同じ空間に密着位相を入れた空間への恒等写像は連続ですが，連続像は連結で，完全不連結ではありません。

連結性に関する概念

連結性に関する概念を列挙しておきましょう。

名称	定義
連結 (connected)	2つの互いに素な開集合 $U,V$ で， $U\cup V=X$ となっているものは存在しない
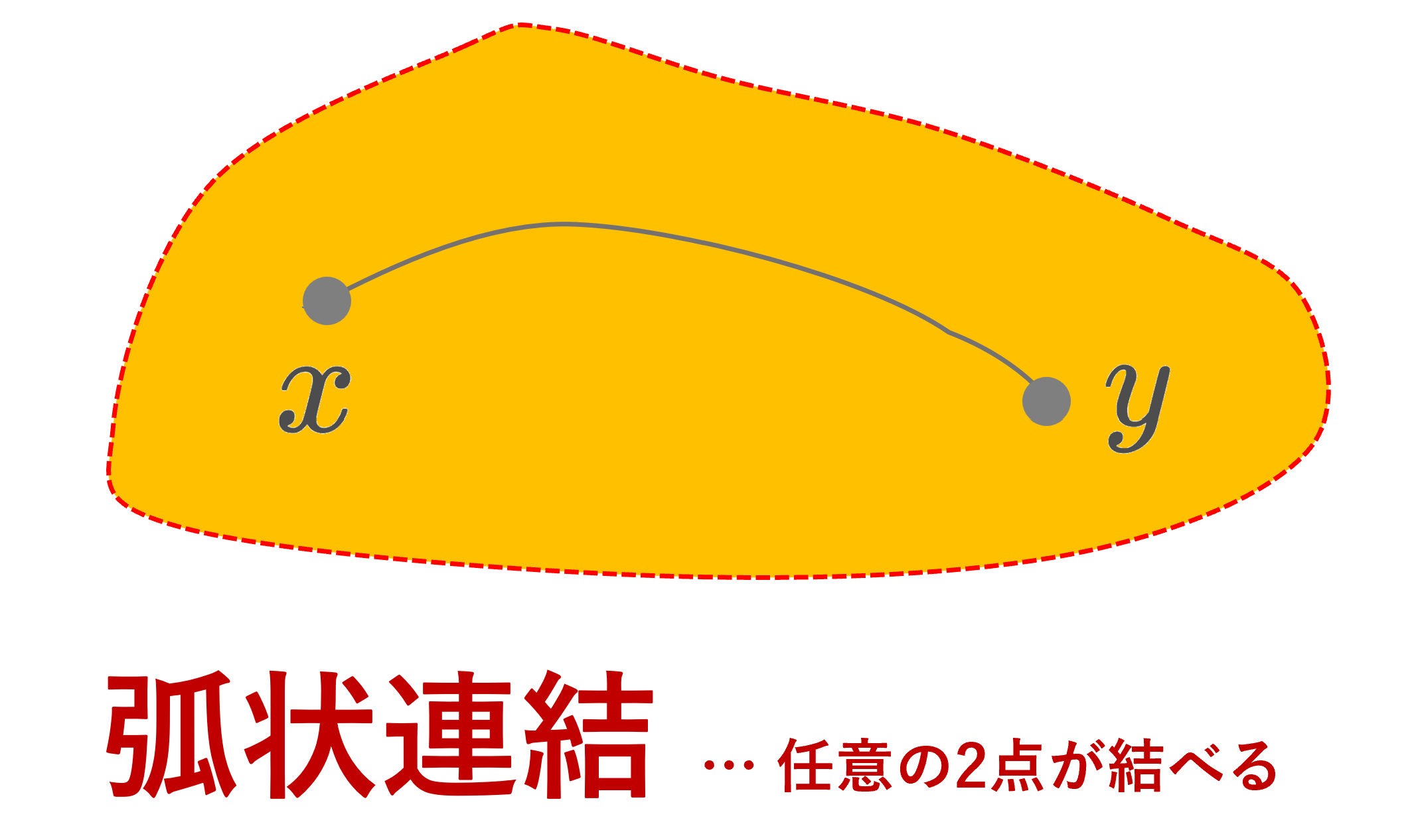
弧状連結 (path connected)	任意の異なる2点 $x,y\in X$ について，ある連続写像 $f\colon [0,1]\to X$ で， $f(0)=x, f(1)=y$ となるものが存在する
弧連結 (arc connected)	上の $f$ として，埋め込みすなわち $f\colon [0,1]\to f([0,1])$ が同相となっているものが常に取れる（※[1]では単に全単射なものが取れるとしている。 $X$ がハウスドルフ ( $T_2$ )なら弧状連結と弧連結は同値）
hyperconnected	任意の空でない2つの開集合が常に共通部分を持つ
ultraconnected	任意の空でない2つの閉集合が常に共通部分を持つ
完全不連結 (totally disconnected)	連結部分集合が1点集合のみ
完全弧状不連結 (totally path disconnected)	弧状連結部分集合が1点集合のみ
局所連結 (locally connected)	全ての点において，連結集合からなる基本近傍系を持つ
局所弧状連結 (locally path connected)	全ての点において，弧状連結集合からなる基本近傍系を持つ
単連結 (simply connected)	$f(0)=f(1)$ をみたす任意の連続写像 $f\colon [0,1]\to X$ が定値写像とホモトピック