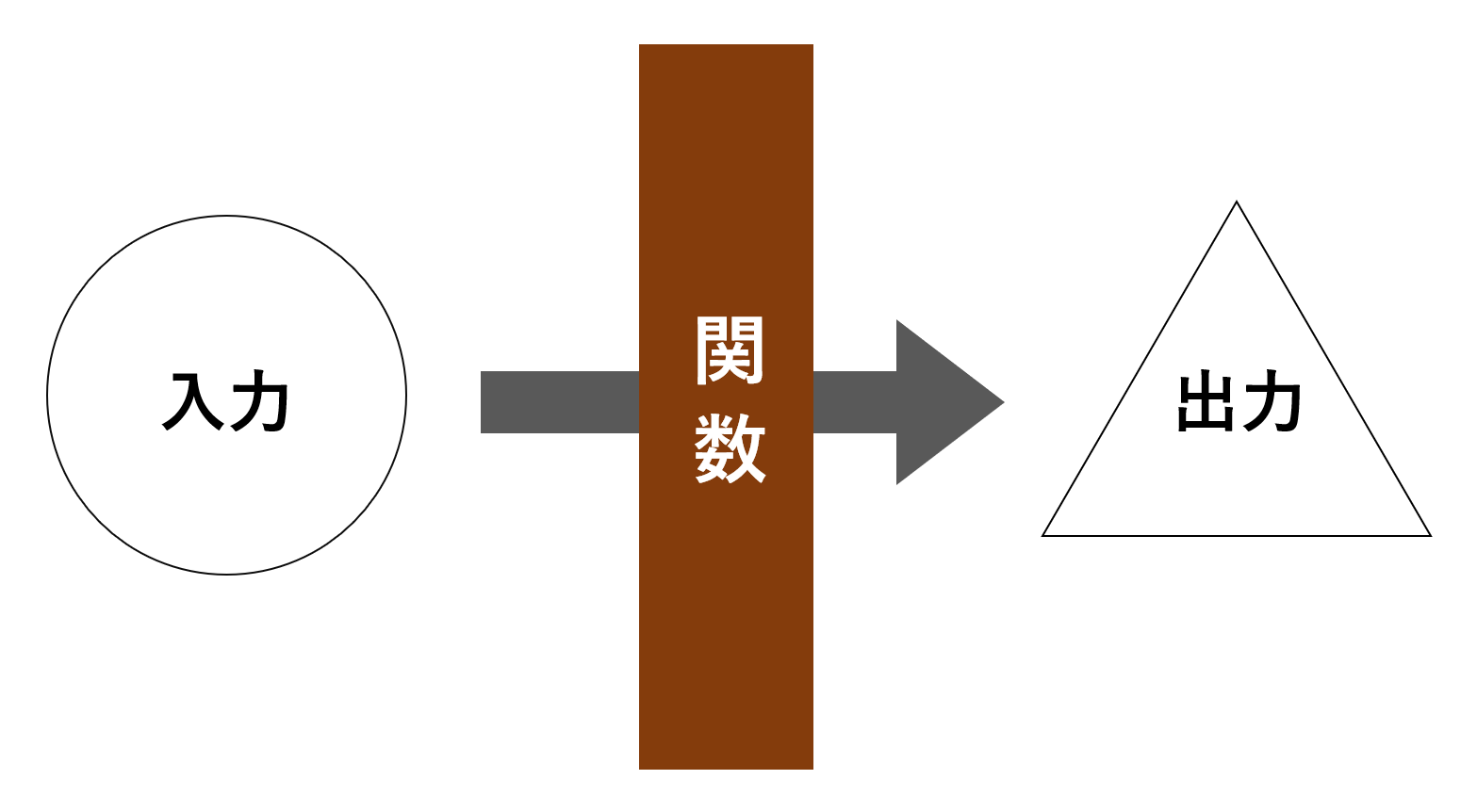
関数(写像)とは,入力を与えるとある特定の出力を一つ返すものである。
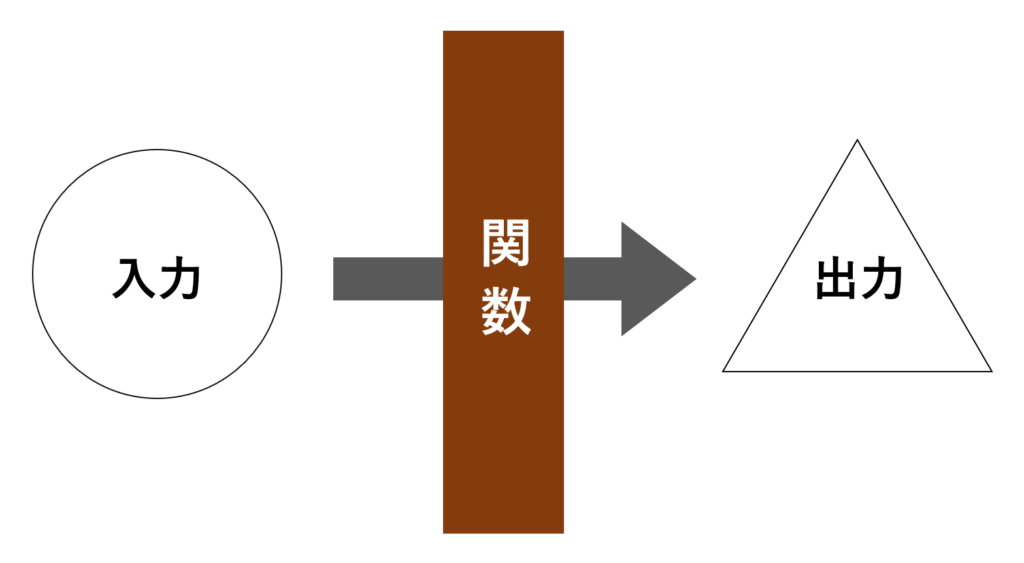
これが,「関数(写像)とは何か」という問いの最も簡単な答えです。これについて,数学的に正しく理解しましょう。
関数・写像の定義と具体例
関数・写像の定義
定義(関数・写像)
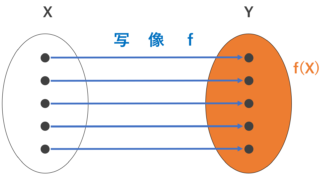
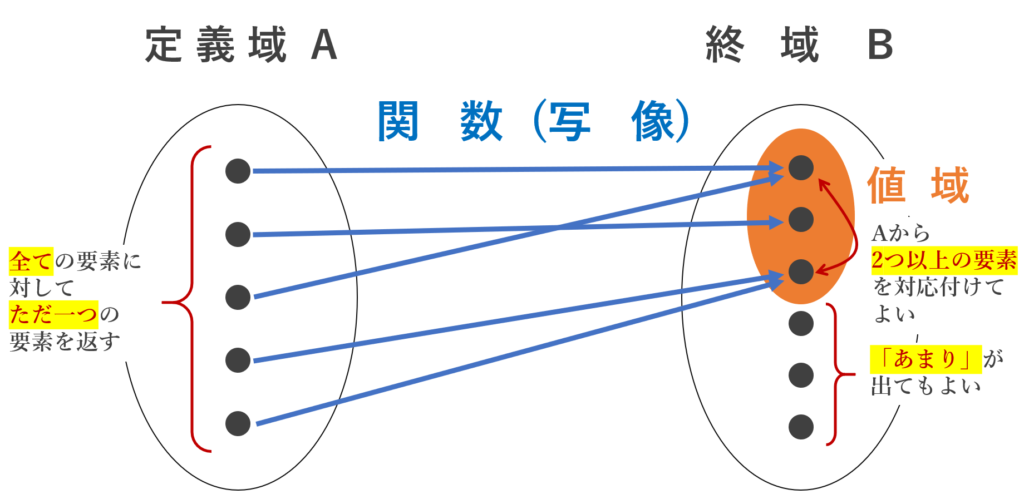
集合 A の全ての要素に対し,その要素を入力すると,集合 B の特定の要素をただ一つ出力するものを関数 (function) または写像 (mapping) という。
このとき, A をその写像の定義域 (始域; domain) といい, B を終域 (codomain) という。
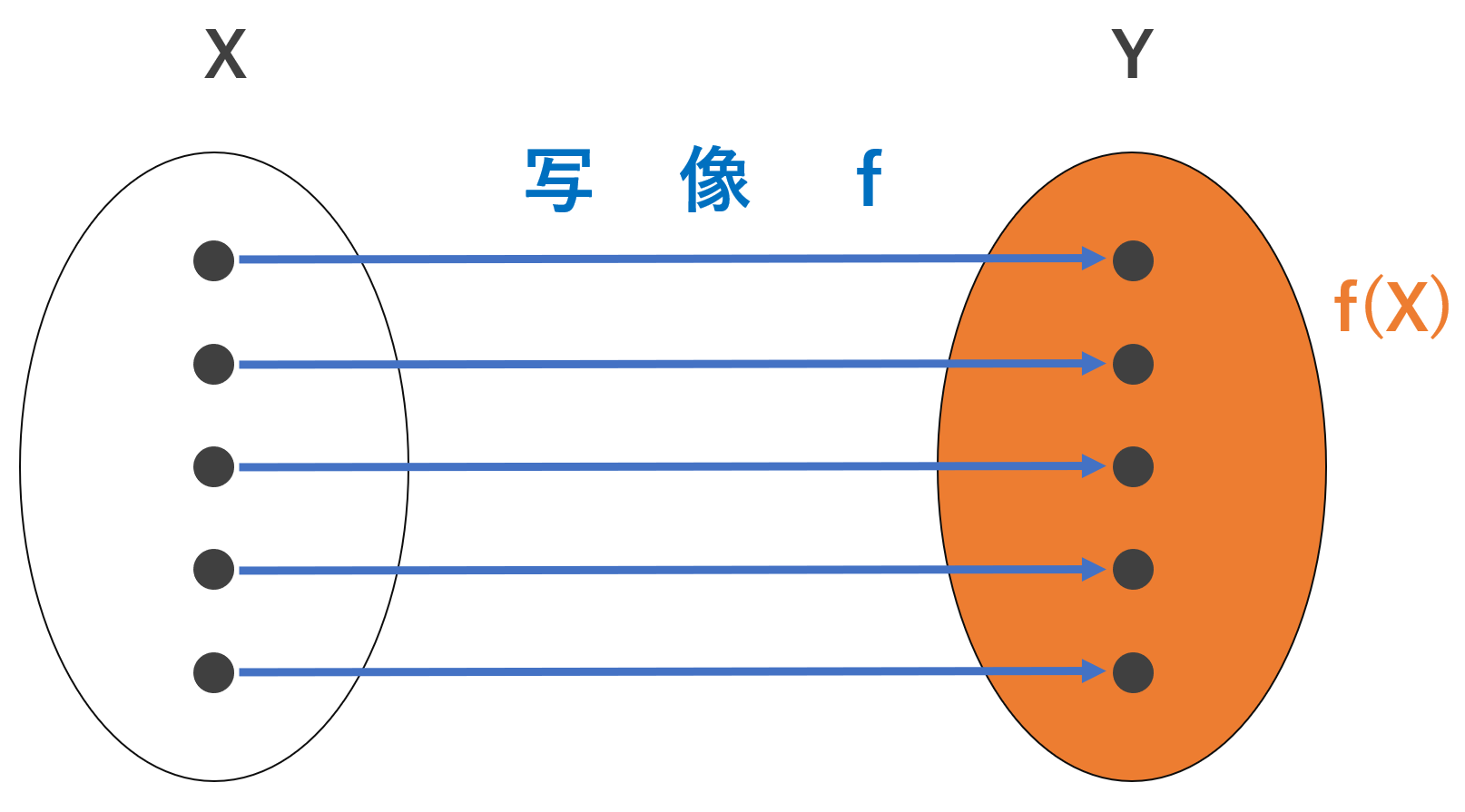
またこのとき, A を入力したときの出力となり得る B の部分集合全体を関数(写像)の値域 (像; range) という。
ここで, A の要素(元)を入力すると, B の要素(元)を返すわけですから, A の各要素を B に対応付けているとみることもできます。
以下で関数(写像)のイメージを挙げます。
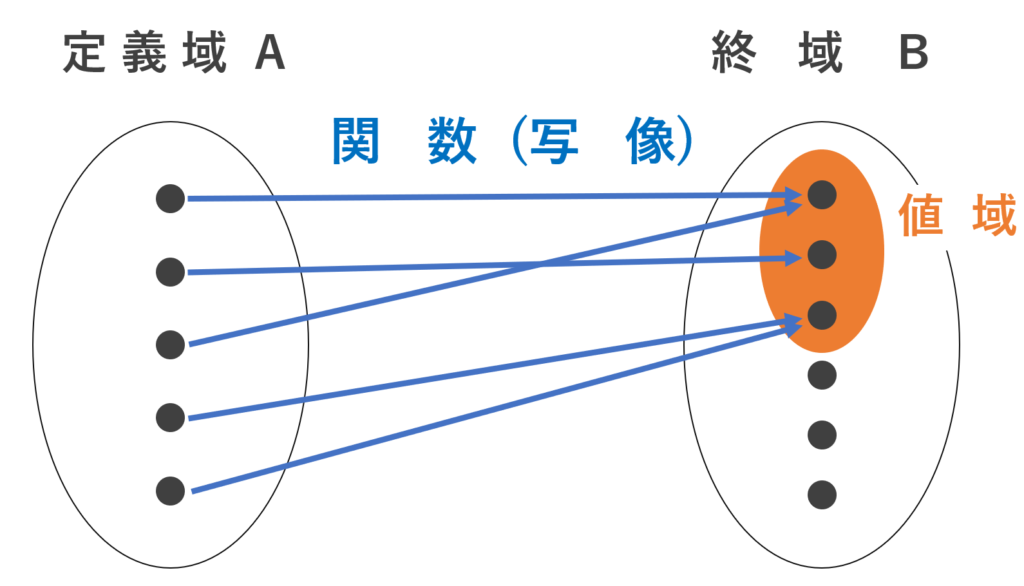
ここで,注意点が3つあります。
ここで,「あまり」とは, A と対応付けされない要素,という意味で用いました。
以下の図を見てください。先ほどの図に注意を添えました。
関数(写像)の具体例
具体例を確認してみましょう。
関数(写像)の具体例
- 英語の小文字を入力すると,その大文字を出力するもの
(たとえば,a -> A, b -> B, …) は,
定義域を「アルファベットの小文字全体の集合」,
終域を「アルファベットの大文字全体の集合(またはそれを含むより大きな集合)」
値域を「アルファベットの大文字全体の集合」
とする関数(写像)である。
- 整数を入力すると,その数が2で割れるとき〇,割れないとき×を出力するもの
(たとえば,2 -> 〇, 5 -> ×) は,
定義域を「整数全体の集合」,
終域を「{〇,×}(またはそれを含むより大きな集合)」
値域を「{〇,×}」
とする関数(写像)である。
- 実数の組 (x, y) を入力すると,その和 x + y を出力するもの
(たとえば (2, 1) -> 3, (0.2, -1) -> -0.8) は,
定義域を「実数の組 (x, y) 全体の集合」,
終域を「実数全体の集合(またはそれを含むより大きな集合)」
値域を「実数全体の集合」
とする関数(写像)である。
それぞれ定義域の入力全てに対し,ただ一つの出力を返していることを確認してください。
また,終域において,「(またはそれを含むより大きな集合)」と書きましたが,これは,終域には「あまり」があっても良いことに起因します。もう一度上の図を見てみてください。
なお,補足的注意ですが,終域が変われば,それはもとの関数(写像)とは別の関数(写像),異なった関数(写像)と考えます。
関数(写像)の表記法と具体例
関数はそれ特有の表し方がありますから,確認していきましょう。
関数(写像)の表記の定義
関数(写像)は関数の英語である function の頭文字をとって, f と表されることが多いです。2つ以上関数(写像)があるときは,以下アルファベット順に f, g, h, \ldots などとします。伝われば文字は何でもいいのですが,あくまで慣習です。もちろん他の文字を使うこともあります。
一方,以下の表記法は重要なので,必ず使いこなせるようになりたいです(ただし,高校生以下ではあまり出てこないかもしれません)。
定義(関数・写像の表記)
定義域が集合 A ,終域が集合 B である関数(写像) f を
\textcolor{red}{f\colon A \longrightarrow B}
とかく。 A の各要素 x \in A に対して,それに対応する B の要素が y \in B であるとき,これを
または,
とかく。すべてまとめて,
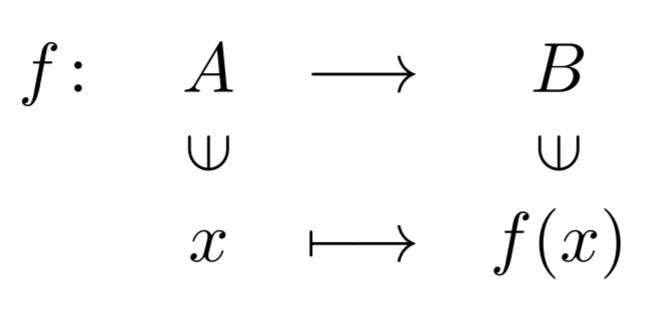
のような表記をすることもある。
また,値域は
\textcolor{red}{ f(A) = \{f(x) \in B \mid x \in A \}}
とかく。
ここでのポイントは,定義域の集合から終域の集合への矢印は単なる矢印であるのに対し,定義域の各要素から対応する終域の要素への矢印は縦棒が一本入っていることです。
たまに縦棒が入っていない文献もありますが,要素から要素への対応は多くの場合,縦棒が入っています。注意しましょう。
関数(写像)の表記の具体例
具体的にさまざまな関数(写像)をさまざまな表記で表してみることで,イメージを膨らませましょう。
なお, \mathbb{R} は実数全体の集合, \mathbb{Z} は整数全体の集合をあらわします。
関数(写像)の表記の具体例
- f\colon \{\text{a, b, c, \ldots, z}\} \longrightarrow \{\text{A, B, C, \ldots, Z}\}
を,英語の小文字を入力すると,その大文字を出力する関数(写像)とする。このとき,
f(\text{a}) = \text{A}, \, f(\text{b}) = \text{B}
であり,値域は \{\text{A, B, C, \ldots, Z}\} である。
- f\colon \mathbb{Z} \longrightarrow \mathbb{Z}
を,整数を入力すると,2で割ったあまりを出力する関数(写像)とする。このとき,
3 \mapsto 1,\, 8 \mapsto 0
であり,値域は \{0, 1\} である。
- f\colon \mathbb{R} \longrightarrow \mathbb{R}
を, f(x) = x^2 と定義する。このとき,
f(0) = 0, \, f(2)= 4
であり,値域は \{x \in \mathbb{R} \mid x \ge 0\} である。
表記に関しては,さまざまな文献をみたり,本サイトのさまざまな記事を眺めることで,段々慣れていきましょう。
関数と写像の違いは?
今まで「関数」と「写像」の2つの言葉を用いてきました。両者の違いはどのようなところにあるのでしょうか。
結論,両者の違いは基本的にないと思って差し支えないです。
強いて言えば,終域が数やそれに関連するものであるとき,「関数」といい,そうでないとき「写像」ということが多いです。ただ,実際のところは曖昧で,英語でも mapping (写像) より function (関数) の方が広く使われている印象があります。
また,「関数」は「函数」と記すこともあります。どちらかというと古い文献に多い印象です。
一方で,慣習によりほとんど「写像」としか言わないもの,「関数」としか言わないものもあります。大学数学における「線形写像」「線形汎関数」「超関数」などがその例です。他にも,関数・写像のことを「作用素」ということもあります。
まとめ・さらなる発展
まとめです。
- 関数または写像とは,ある集合 A の全ての要素に対して, B の要素をただ一つ返すもの
- このとき, A を定義域, B を終域,関数の対応先となり得る B の部分集合を値域という
関数(写像)のイメージ図を再掲しておきます。

ここで,さらに進んだ概念を少しだけ紹介します。
- 全射(上への写像) …… 終域に「あまり」がないもの
- 単射(1対1写像) …… A から2つ以上の要素の対応付けがないもの
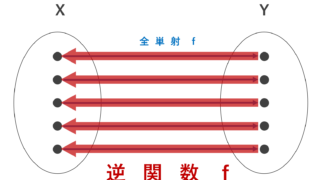
- 全単射 …… 全射かつ単射であるもの
- 逆関数・逆写像 …… 全単射のときに対応関係を入れ替えた関数・写像
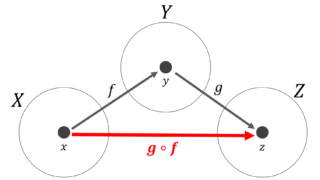
- 合成関数・合成写像 …… 2つ以上の関数を「組み合わせて」できた関数・写像
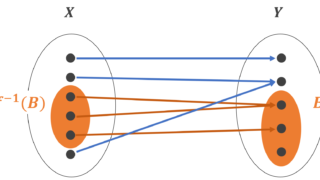
- 逆像 …… B の部分集合を指定したとき,そこにうつる A の部分集合
これらについては,以下の4つの記事で解説しています。どれも大事な概念ですから,ぜひ参照してみてください。
関数(写像)は数学において必須の概念ですから,慣れていきましょう。
おつかれさまでした。