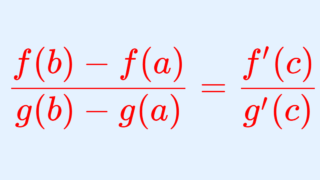積分バージョンの平均値の定理について,その主張と,証明を2通り述べます。
積分の平均値の定理
積分の平均値の定理
f は [a,b] 上積分可能で, m \le f(x) \le M \,\,(a \le x\le b) とすると,
\lambda = \frac{1}{b-a} \int_a^b f(x)\, dx
となる m\le \lambda \le M が存在する。特に, f が連続ならば,
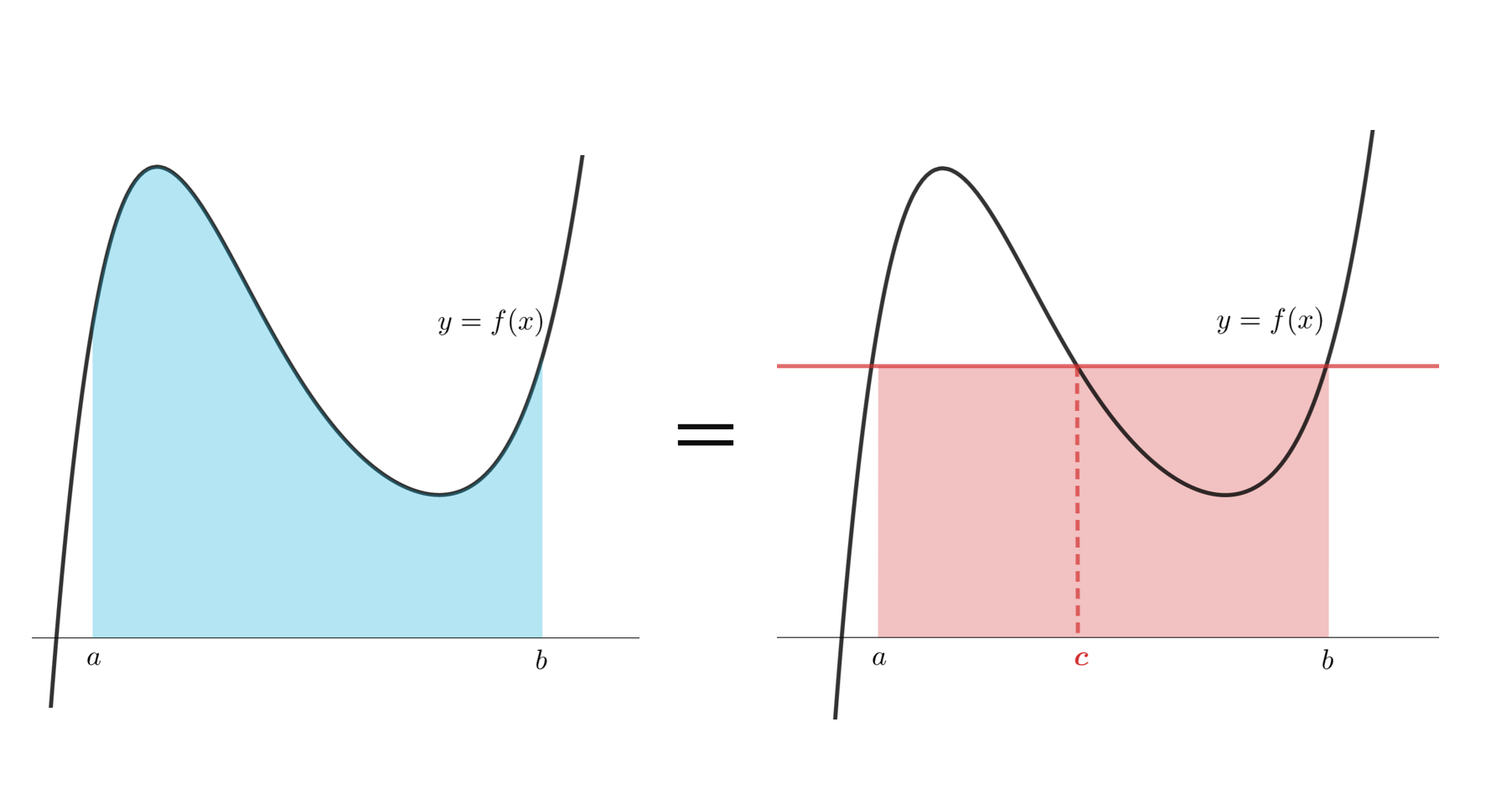
となる a<c<b が存在する。
式の右辺は「積分の平均」と言えますね。それが, f 上のある一点 c を用いて f(c) と表せるというわけです。
これは,以下の2つの部分の面積が等しいことを意味します。
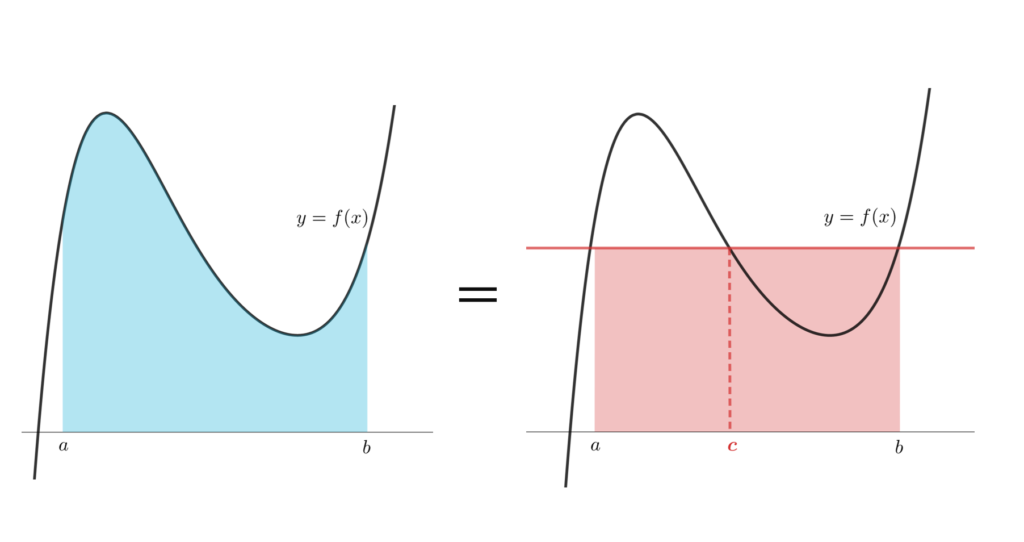
積分の平均値の定理の証明
早速証明しましょう。証明は
- 「最大値・最小値定理」と「中間値の定理」を用いた証明
- 微分における平均値の定理に帰着させる証明
の2通りで行いましょう。
最大値・最小値定理と中間値の定理を用いた証明
表題の通り,証明には「最大値・最小値定理」と「中間値の定理」を用います。それぞれについては,
で解説しています。
証明
m\le f(x)\le M より,
m(b-a) \le \int_a^b f(x) \, dx \le M(b-a)
が成り立つ。よって
とおけば,題意をみたす。 f が連続のときは,最大値・最小値定理により,最大値を M ,最小値を m と思うと,上の \lambda について, m \le \lambda \le M であるから,中間値の定理により, f(c) = \lambda となる a<c<b が存在する。
証明終
微分の平均値の定理を用いた証明
もう一つは,微分における平均値の定理を用いる証明です。こちらは f は連続とした後半の主張のみ証明します。
証明
F(x) = \int_a^x f(y) \, dy \,\, (a\le y \le x) とすると, f は連続なので, F'(x) = f(x) が成立する。微分における平均値の定理により,
\frac{F(b) - F(a)}{b-a} = F'(c)
となる a<c<b が存在する。これを書き直すと,
を得る。
証明終
その他の平均値の定理
平均値の定理といわれるその他のものについて紹介しておきましょう。
微分における平均値の定理
証明内ですでに用いましたが,改めて微分における平均値の定理の主張を確認してみましょう。
ラグランジュの平均値の定理 (Lagrange’s mean value theorem)
関数 f は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能であるとする。このとき,
\color{red} \frac{f(b)-f(a)}{b-a} = f'(c) , \quad a < c< b
となる c が存在する。
「平均値の定理」といわれると真っ先に思いつくのがこれかもしれません。少なくとも高校生はそうでしょう。これに関しては,以下の記事で解説しています。
コーシーの平均値の定理
コーシーの平均値の定理は,上の微分における平均値の定理(ラグランジュの平均値の定理)を一般化したものと言えます。
コーシーの平均値の定理 (Cauchy’s mean value theorem)
関数 f,g は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能であるとする。このとき, g'(x) \ne 0 \,\,(a < x < b) ならば,
\color{red} \frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(c)}{g'(c)} , \quad a < c< b
となる c が存在する。
これについては,以下の記事で解説しています。