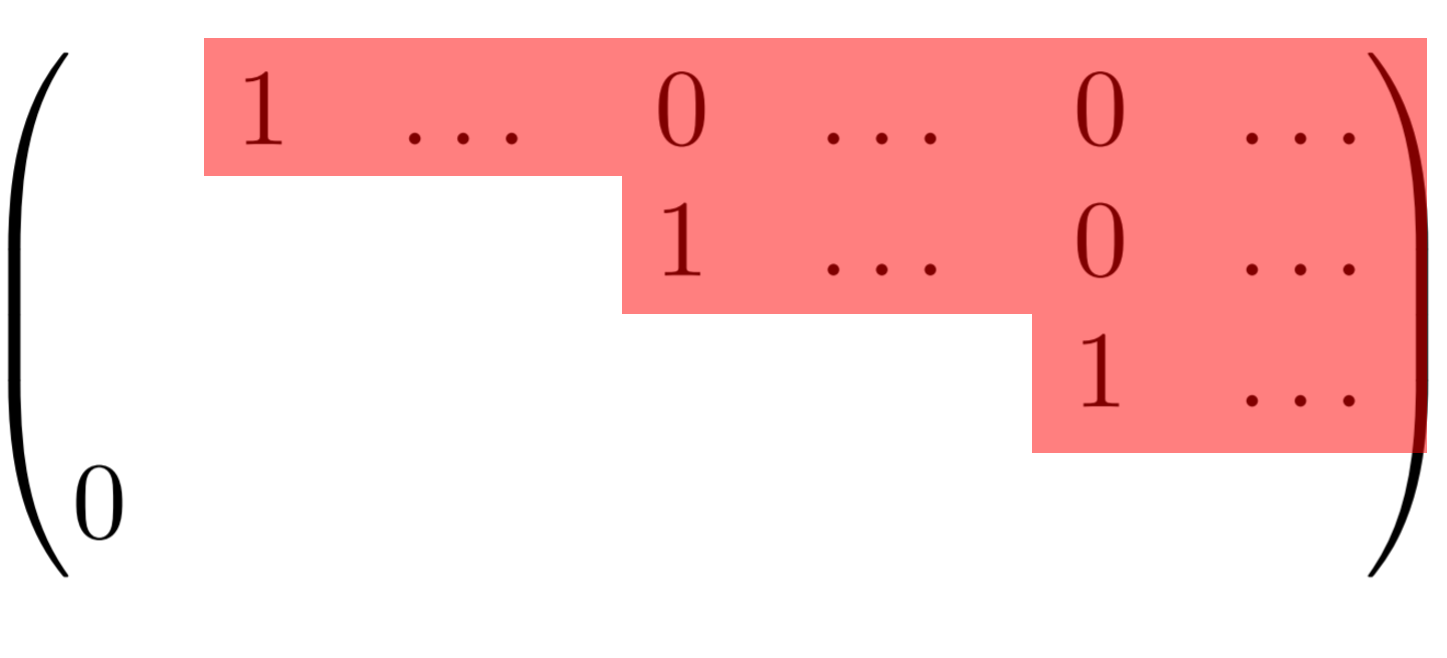
行列における「階段行列」について,定義と例を確認し,さらにその作り方を,分かりやすく図解しながら述べましょう。
階段行列の定義と例
まずは,階段行列の定義と例を,順番に述べましょう。
階段行列の定義
定義(階段行列)
m \times n 行列の第 i 行について,第 1 列から考えて初めて 0 でない成分が出てくる列を第 d_i 列とする。ただし,第 i 行がすべて 0 のときは d_i = n +1 と約束する。
\small \color{red}\boldsymbol{d_1 < d_2 < \dots < d_m }または
\small \color{red}\boldsymbol{d_1 < d_2 < \dots < d_i < d_{i+1} = \cdots = d_m=n+1}
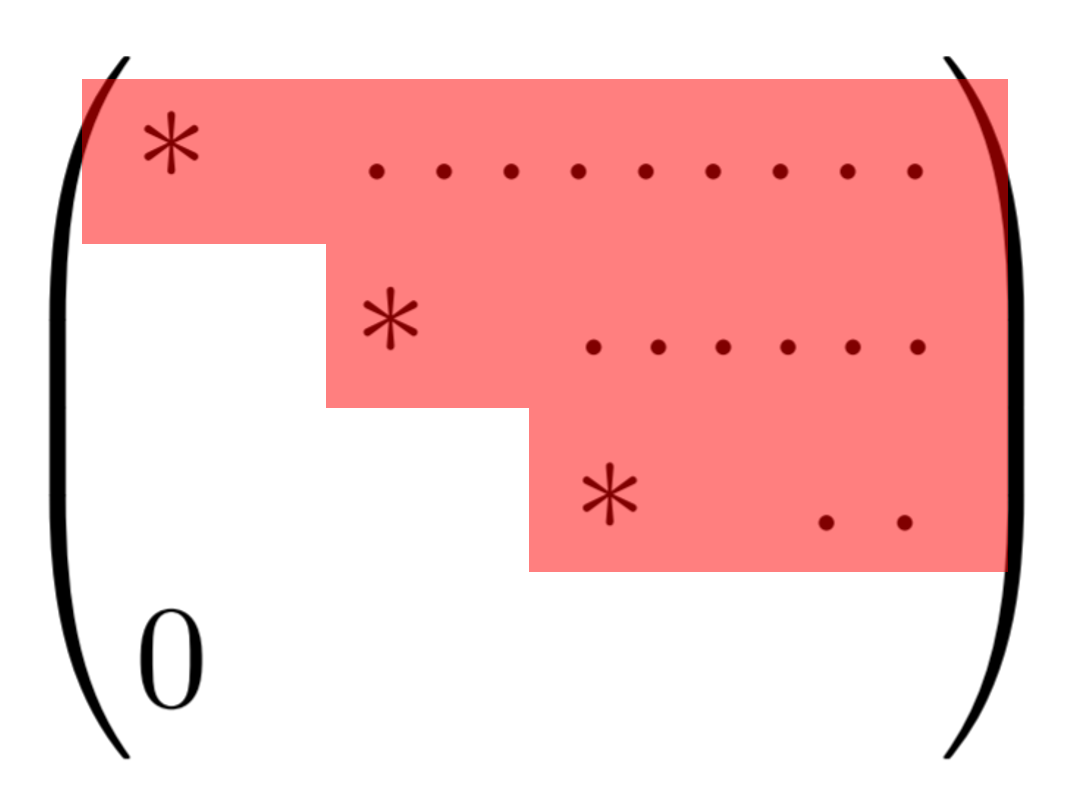
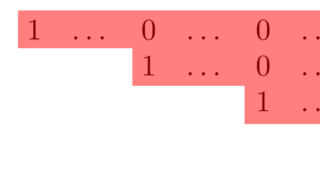
であるとき,これを階段行列 (step matrix) という。図で描くと以下のような行列のことである。
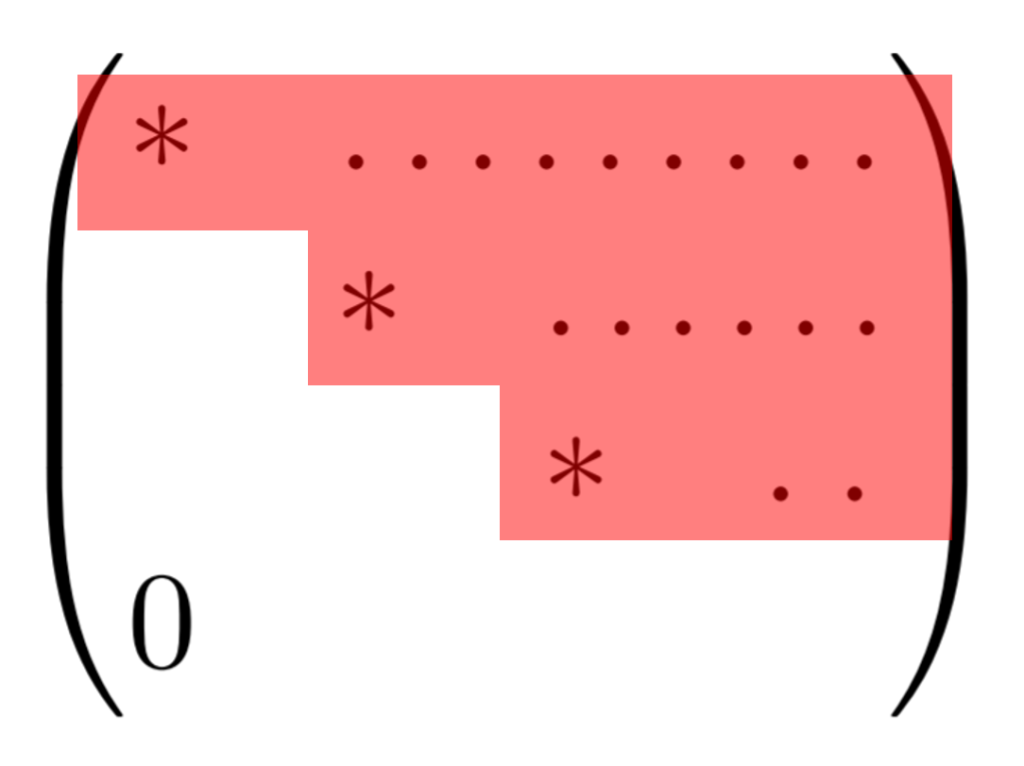
ただし, * は 0 でない成分を指す。
0 でない成分が階段状に並んでいるから,「階段行列」といわれるんですね。
なお, * より右側の成分に 0 が入っていても構いません。たとえば,単位行列は階段行列の一種です。
階段行列の例
階段行列の例をいくつか列挙しておきましょう。
階段行列の例
- \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix}
- \begin{pmatrix} 1 & 1& 1 & 3 \\ 0 & 0 & 4 & 2 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}
- \begin{pmatrix} 1 & 2 & 0 & 3 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}
- \begin{pmatrix} 1 & 2& 3 & 0 & 0 \\ 0 & 1 & 2 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{pmatrix}
- \begin{pmatrix} 0 & 0 & 1 & 2 & 3 \\ 0 & 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 & 1 \end{pmatrix}
- 単位行列
- 対角行列
- 上三角行列
階段行列と行列の階数(rank)
階段行列には,以下の性質があります。
定理(階段行列の段数と行列の階数の一致)
階段行列における階段の段数は,行列の階数 \operatorname{rank} と一致する。
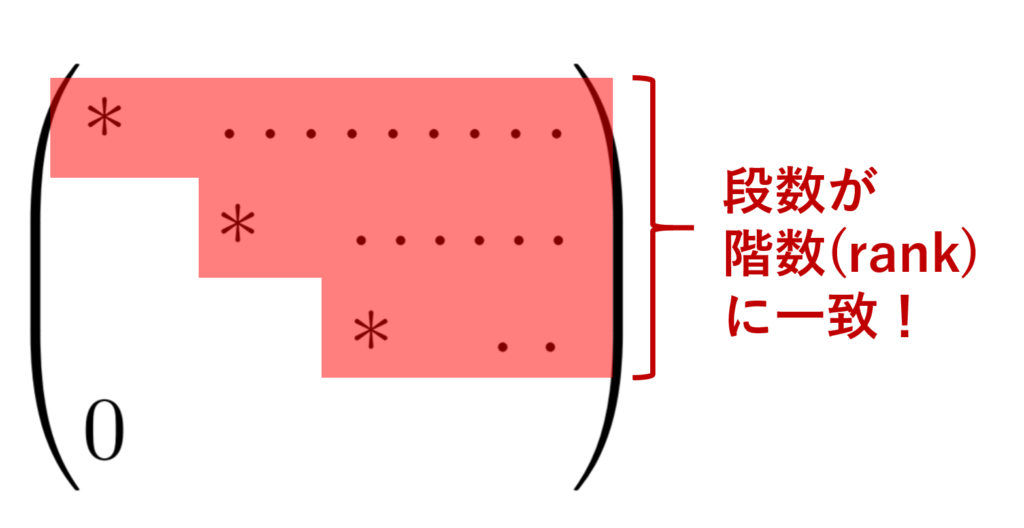
この定理より,階段行列に変形することは,行列の階数を求めるうえでも有用であることが分かります。基本的に,行列の階数を求めたければ,階段行列に変形してみればよいわけです。
階段行列の行基本変形による作り方
階段行列を作るにあたって,以下の定理が知られています。
定理(階段行列は行基本変形によって作れる)
任意の行列は,行基本変形を用いて階段行列に変形できる。
「行基本変形」とは以下の3つの変形のことです。
- ある行の \boldsymbol{c} 倍を他の行に加えること
- 2つの行を入れ替えること
- ある行を \boldsymbol{ c \ne 0 } 倍すること
より詳しくは,行列の基本変形に関する以下の記事を確認してください。
これを用いて,階段行列を作ることを考えてみましょう。
階段行列の作り方の手順
作り方はいたって機械的です。
階段行列の作り方の手順
- まず第 1 列に着目する。第 1 列が 0 でない行があれば,その行を行の交換によって第 1 行に移動させる。そして,その行以外の第 1 列が 0 になるように変形する。
- 第 1 行,第 1 列は無視し,それ以外の (m-1) \times (n-1) 行列に対し,1.と同じ操作を行う。
- 2.と同様の操作を (m-2) \times (n-2) 行列, (m-3) \times (n-3) 行列…… に対して順番に続ける。
具体的に考えてみましょう。
階段行列の作り方の具体例
例題
\begin{pmatrix}1 & 1& 3 & 5\\ 2 & 3 & 7 & 8 \\ 1 & 7 & 0 & 0 \end{pmatrix} を,行基本変形のみを用いて階段行列にせよ。
答えの一例を記載しておきます。
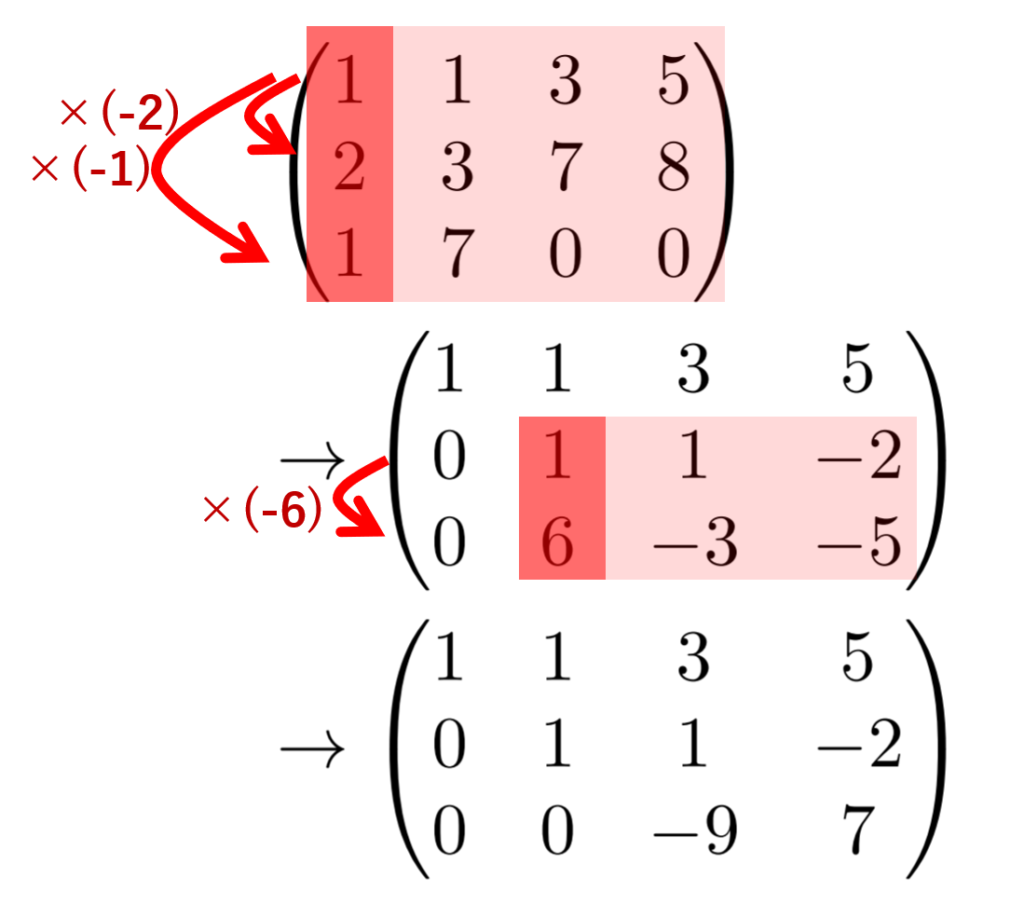
無事,階段行列にできましたね。
なお,一つの行列に対して,階段行列の変形の仕方は一通りではないことに注意してください。これ以外の階段行列も作れます。
RREF行列
階段行列のうち, *=1 かつ * の上の成分がすべて 0 である行列をRREF行列といい,行基本変形のみを用いてこの形に変形することを行列の簡約化といいます。これについては,以下の記事を参照してください。