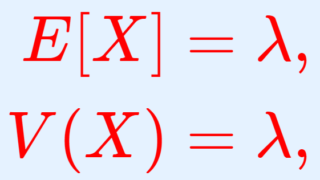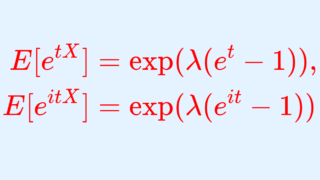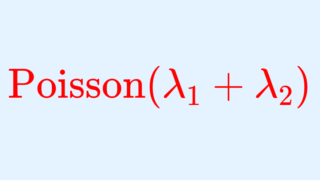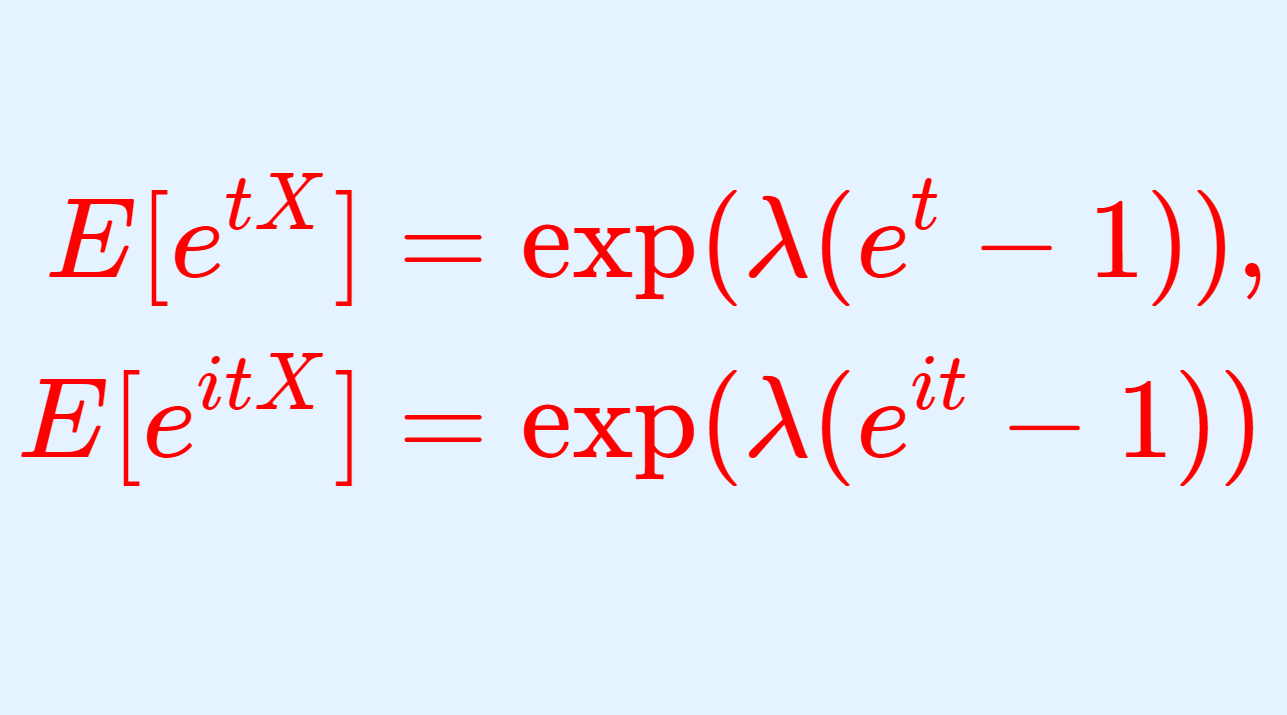ポアソン分布とは主に,まれな事象が一定時間に起こる回数を表す確率分布で, P(X=k) = \dfrac{\lambda^k}{k!}e^{-\lambda } \,\,(k=0,1,2,\ldots) と定義されます。これについて,その定義と具体例,性質について詳しく掘り下げましょう。
ポアソン分布の定義
まずは,ポアソン分布の定義を述べ,その確率をグラフを描いてみましょう。
定義(ポアソン分布)
X を確率変数, \lambda > 0 とする。 k=0,1,2,\ldots に対し,
\color{red} P(X=k) = \frac{\lambda^k}{k!}e^{-\lambda }
が成り立つとき, X はパラメータ \lambda のポアソン分布 (Poisson distribution) に従うという。本記事では,これを \color{red}X\sim \operatorname{Poisson}(\lambda) とかくことにする。
まず注意ですが, e^x のマクローリン展開は,\displaystyle e^x = \sum_{n=0}^\infty \frac{x^n}{n!} ですから,
\begin{aligned}P(X=0,1,2,\ldots) &= \sum_{k=0}^\infty P(X=k) \\ &= \sum_{k=0}^\infty \frac{\lambda^k}{k!}e^{-\lambda } \\ &= e^{\lambda} e^{-\lambda} = 1 \end{aligned}
となって, P(X=0,1,2,\ldots) = 1 となりますね。
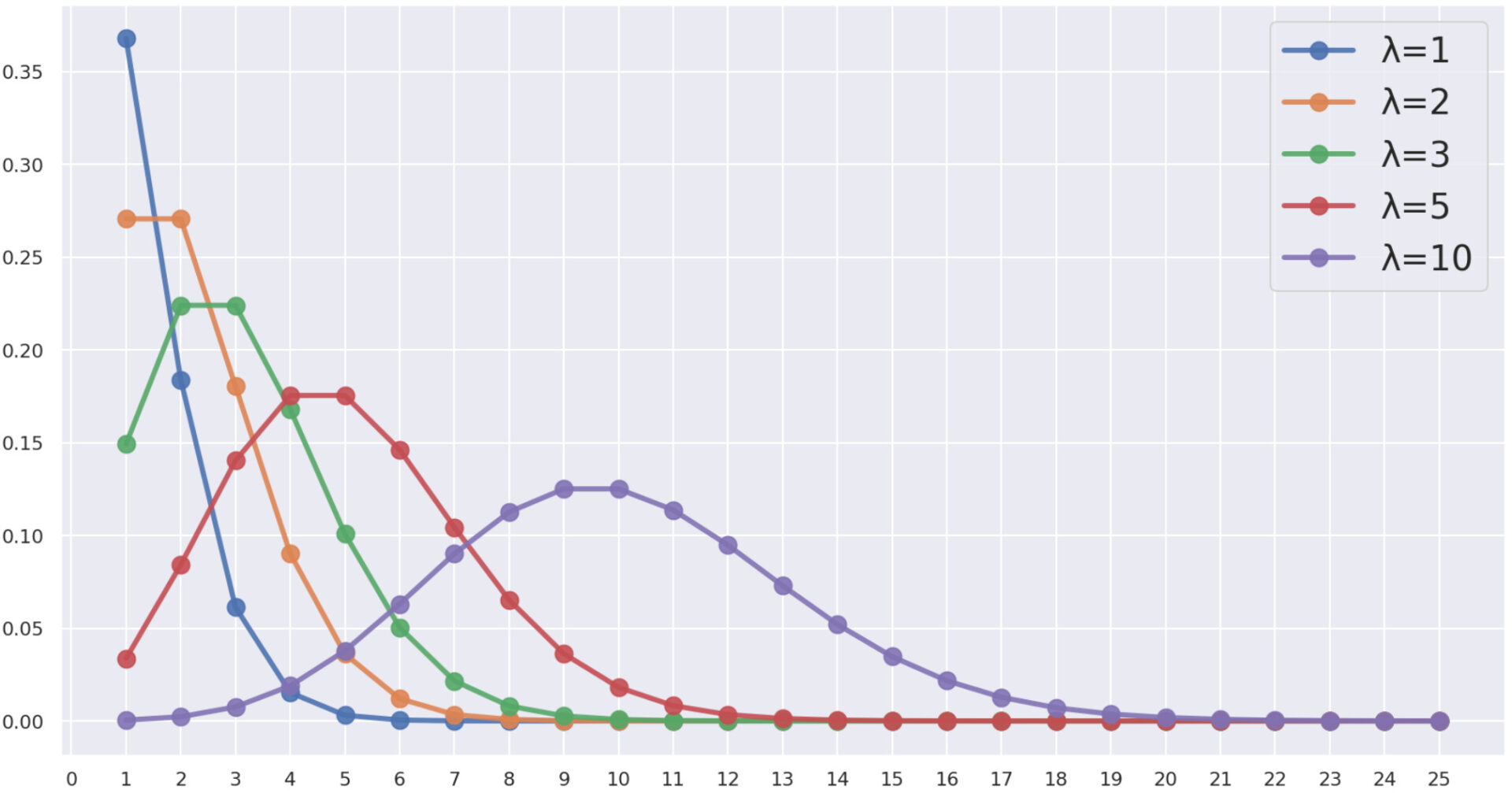
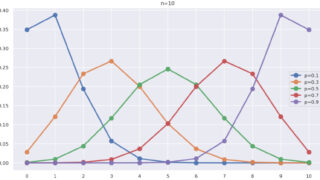
\lambda を変えて,ポアソン分布の確率(質量)関数 P(X=k) \,(k=0,1,2,\ldots) を図示すると,以下のようになります。
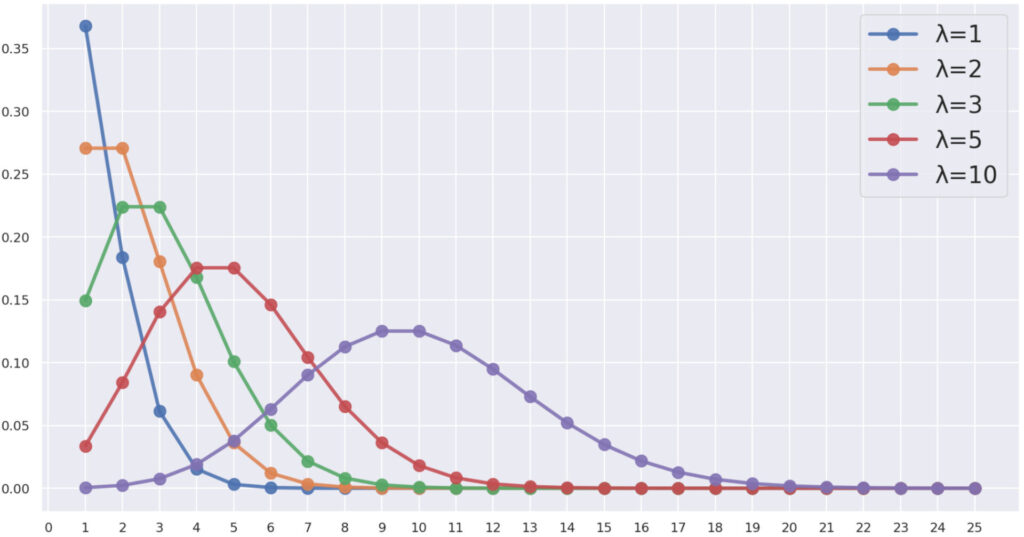
見ての通り, \lambda が大きいほど,山が右に推移するんですね。
ポアソン分布の例
ポアソン分布は,(まれに起こる)ある事象に対し,その事象が一定時間に何回発生したかを表す分布として,よく用いられます。たとえば,以下のようなものです。
- コールセンターに1時間当たりかかってくる電話の数
- 某交差点で1日当たりに事故が起こる回数
- あるコンビニに1日当たりに来る客数

なお,ポアソン分布でモデル化されるもののポイントは, 1 回その事象が発生したからと言って,次発生するかどうかに影響を与えないという点です。たとえば,コールセンターに1回電話があったからと言って,その1時間の間にもう1回電話がかかってこないとは限りません。
また,「一定時間に起こる回数(や人数)」をモデル化したものと説明しましたが,「回数(や人数)」以外をモデル化することもあります。
ポアソン分布の性質
さて,今回紹介するポアソン分布の性質を,最初に列挙することにしましょう。
| ポアソン分布 \operatorname{Poisson}(\lambda) | |
|---|---|
| 確率 | P(X=k) = \dfrac{k^\lambda}{k!}e^{-\lambda}\;\,(k=0,1,2,\ldots) |
| 確率分布の型 | 離散型 |
| 累積分布関数 | \begin{dcases}0 & x<0, \\ \sum_{k=0}^{\lfloor x \rfloor} \dfrac{k^\lambda}{k!}e^{-\lambda} & x\ge 0 \end{dcases} |
| 期待値 E[X] | \lambda |
| 分散 V(X) | \lambda |
| 標準偏差 \sqrt{V(X)} | \sqrt{\lambda} |
| 積率母関数(モーメント母関数) E[e^{tX}] | \exp (\lambda(e^t-1)) |
| 特性関数 E[e^{itX}] | \exp(\lambda(e^{it}-1)) |
| 再生性 | \begin{aligned}&X_1 \sim \operatorname{Poisson}(\lambda_1), X_2 \sim \operatorname{Poisson}(\lambda_2) \\ &\implies X_1+X_2 \sim \operatorname{Poisson} (\lambda_1+\lambda_2)\end{aligned} |
| 指数分布との関係 | \sup\{k\mid Y_1 +\dots + Y_k \le 1 \}\, (Y_k \sim \operatorname{Exp}(\lambda)) |
| 二項分布との関係(ポアソンの少数の法則) | \displaystyle \lim_{n\to\infty} Y_n \;(Y_n \sim B(n, p_n)\, \lim_{n\to\infty}np_n=\lambda) |
累積分布関数以降について,詳しく掘り下げていきましょう。
ポアソン分布の累積分布関数(分布関数)
ポアソン分布の累積分布関数(分布関数)は,
\begin{aligned} F(x) &= P(X\le x) \\ &= \begin{dcases}0 & x<0, \\ \sum_{k=0}^{\lfloor x \rfloor} P(X=k) & x\ge 0 \end{dcases} \\ &=\begin{dcases}0 & x<0, \\ \sum_{k=0}^{\lfloor x \rfloor} \dfrac{k^\lambda}{k!}e^{-\lambda} & x\ge 0 \end{dcases} \end{aligned}
ですね。ただし, \lfloor x \rfloor は床関数(ガウス記号)を表します。
図で描くと,以下のようになります。(※ 以下は模式的なものであり,実際は,床関数(ガウス記号)のグラフのような,不連続なものです。)
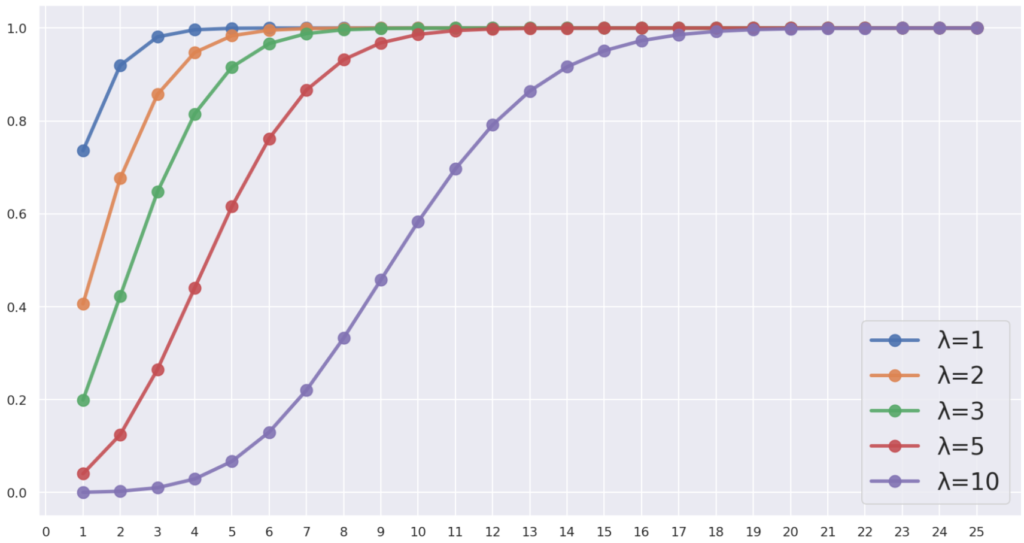
\lambda が大きいほど,グラフが下に来るわけですね。
ポアソン分布の期待値(平均)・分散・標準偏差
定理(ポアソン分布の期待値・分散・標準偏差)
X\sim \operatorname{Poisson}(\lambda) とする。このとき,X の期待値(平均)・分散・標準偏差はそれぞれ
\color{red}\begin{aligned} E[X] &= \lambda, \\ V(X)&= \lambda, \\ \sqrt{V(X)} &= \sqrt{\lambda} \end{aligned}
となる。
期待値も分散も,両方 \lambda になるんですね。この証明については,以下で行っています。
ポアソン分布の積率母関数(モーメント母関数)・特性関数
定理(ポアソン分布の積率母関数・特性関数)
X\sim \operatorname{Poisson}(\lambda) とする。このとき,X の積率母関数(モーメント母関数)・特性関数はそれぞれ
\color{red}\begin{aligned} E[e^{tX}] &= \exp (\lambda(e^t-1)), \\ E[e^{itX}]&= \exp(\lambda(e^{it}-1)) \end{aligned}
となる。
\exp x = e^x ですから,たとえば \exp (\lambda(e^t-1)) = e^{\lambda(e^t-1)} となります。累乗が二回出てきますから,こういうかき方はややこしいので, \exp を用いて記述しています。
これの証明については,以下で解説しています。
ポアソン分布の再生性
定理(ポアソン分布の再生性)
\lambda_1, \lambda_2> 0 とし, X_1 \sim \operatorname{Poisson}(\lambda_1), \, X_2 \sim \operatorname{Poisson}(\lambda_2) を独立とする。このとき,
\color{red} X_1 + X_2 \sim \operatorname{Poisson}(\lambda_1+\lambda_2)
である。
同じ分布族の独立な確率変数を2つ足すと,また同じ分布族に属するとき,これを分布の再生性 (reproductive property) といいます。ポアソン分布や正規分布は,再生性をもつ分布として有名です。
これについては,以下で証明しています。
ポアソン分布と指数分布との関係
定理(ポアソン分布と指数分布との関係)
Y_k \sim \operatorname{Exp}(\lambda) \;\; (k=1,2,3,\ldots) を独立な指数分布とし, X \sim \operatorname{Poisson}(\lambda) とする。このとき,
\color{red} X\stackrel{\mathrm{d}}{=} \sup\{k\in\mathbb{N} \mid Y_1 + Y_2+\dots + Y_k \le 1 \}
である。ただし, \stackrel{\mathrm{d}}{=} は分布の意味で等しいことを意味する。
ポアソン分布と指数分布は,同じような事象の,見方が違うものと言えます。
例を挙げると,コールセンターにおいて「次に電話が来るまでの時間」は指数分布でモデル化され,「ある一定時間に電話が来た回数」はポアソン分布でモデル化されるといった具合です。以下がその一例です。
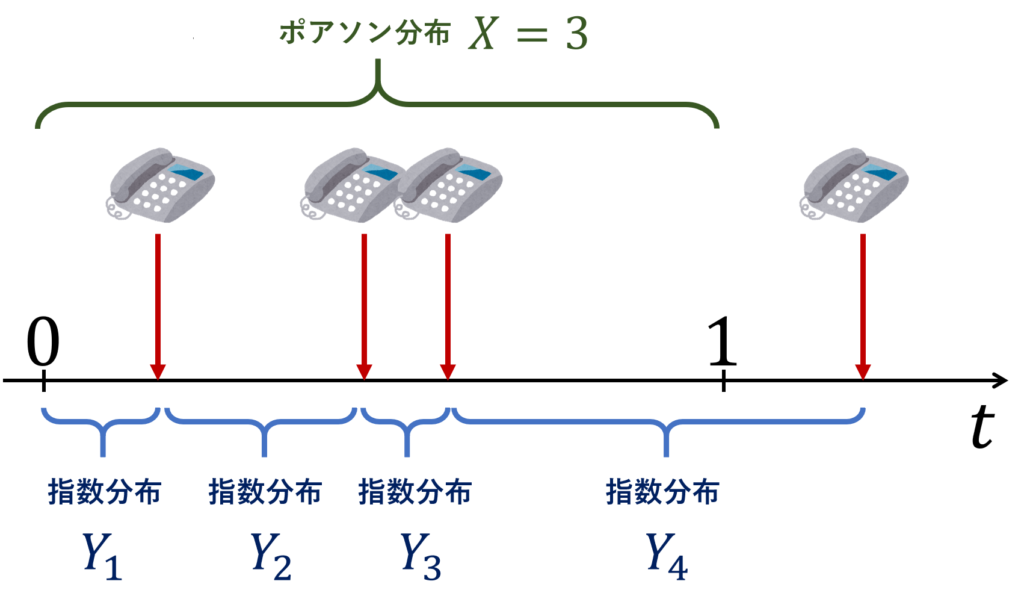
指数分布は,無記憶性をもつ唯一の連続型確率分布です。これについては,以下の記事を参照してください。
二項分布との関係~ポアソンの少数の法則~
ポアソン分布は,二項分布の極限として得ることが可能です。以下の定理を見てください。
定理(ポアソンの少数の法則)
\lambda>0 とし, X_n \sim B(n, p_n ) とする。ただし, \{p_n\} は \lim_{n\to\infty}np_n = \lambda をみたす (0, 1 ) 値の数列である。
このとき, X_n はパラメータ \lambda をもつポアソン分布に分布収束する。すなわち, k=0,1,2,\dots に対し,
\color{red} \lim_{n\to\infty}P(X_n =k) = e^{-\lambda} \frac{\lambda^k}{k!}.ラフに言うと, n が十分大きく, p_n が十分小さいとき,二項分布はポアソン分布で近似できるということですね。