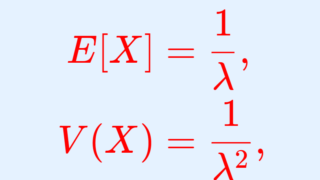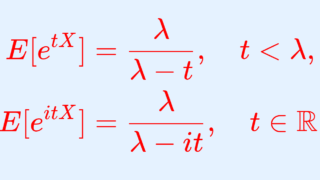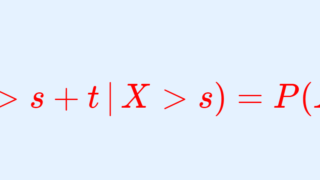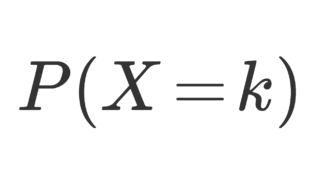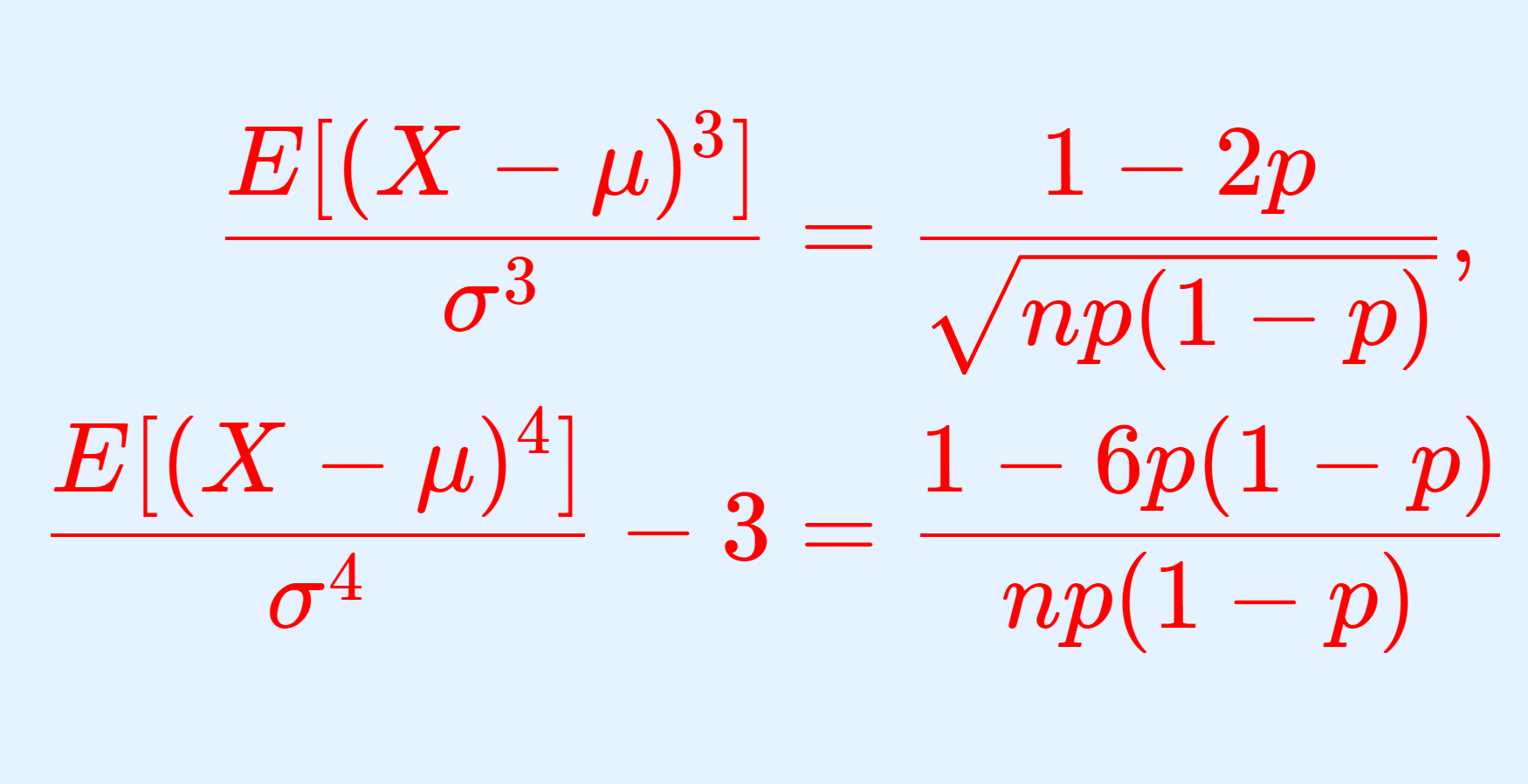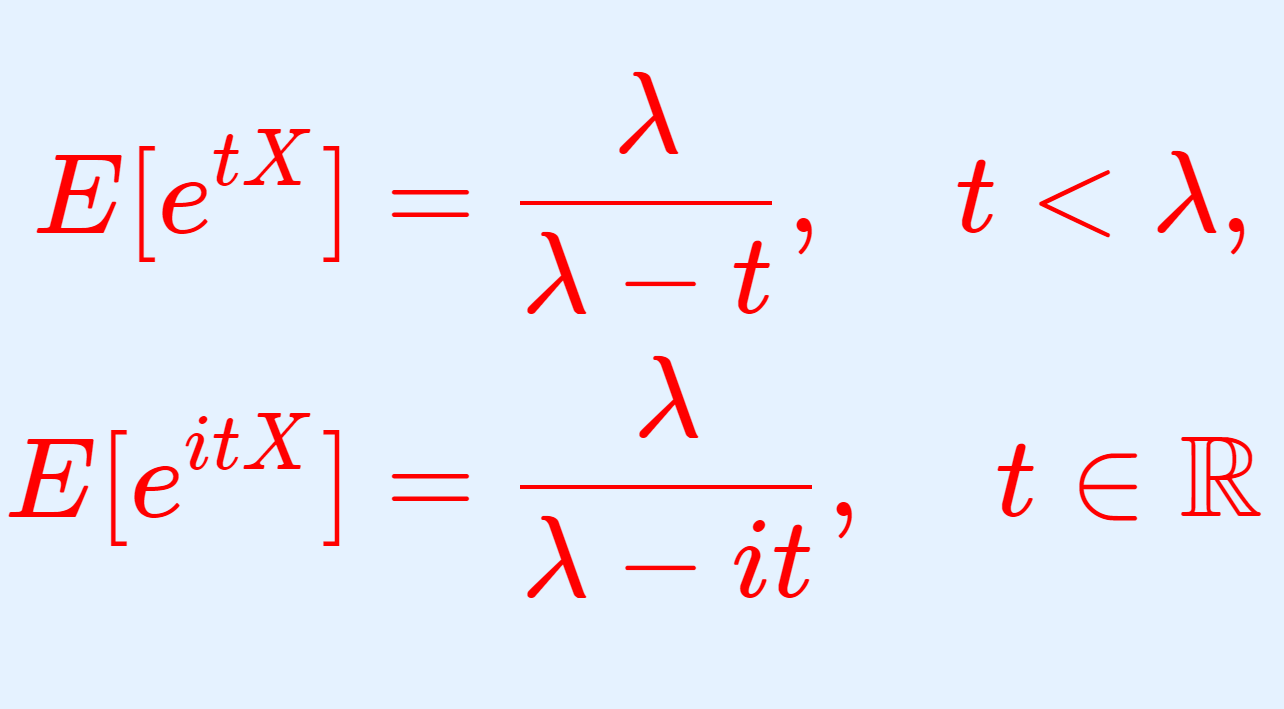指数分布は,確率が指数関数を用いて表現される,「無記憶性」をもつ唯一の連続型確率分布で,その確率密度関数は p(x) = \lambda e^{-\lambda x} で与えられます。これについて,その定義と具体例,性質をまとめて紹介しましょう。
指数分布の定義
定義(指数分布)
\lambda > 0 とする。確率変数 X の確率密度関数が
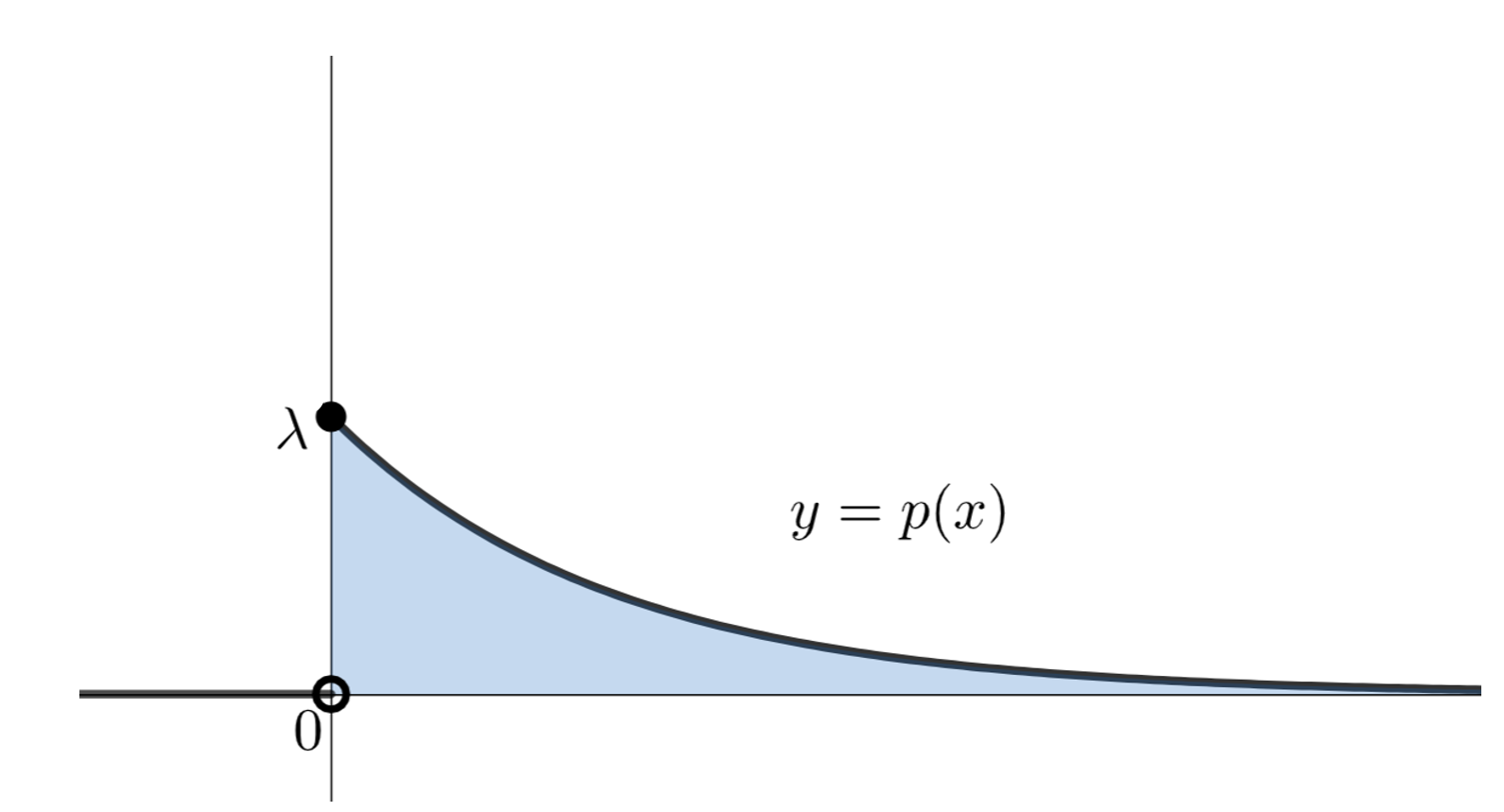
\color{red}p(x) = \begin{cases} \lambda e^{-\lambda x } & x\ge 0,\\ 0 & x<0 \end{cases}
となるとき,X は,パラメータ \lambda の指数分布 (exponential distribution) に従うといい, \color{red} X\sim \operatorname{Exp}(\lambda ) と表す。
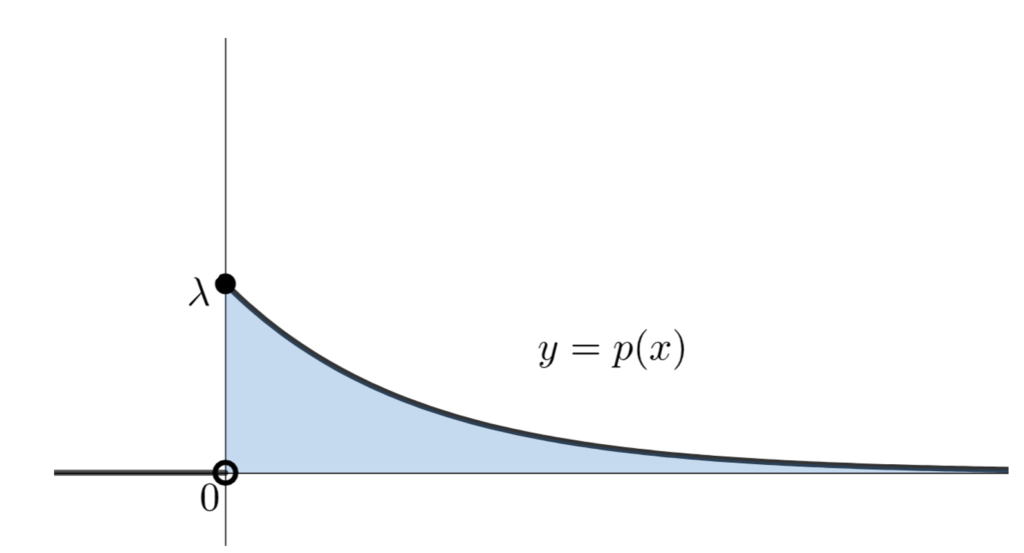
確率密度関数が p(x) とは,すなわち,
P(X\in A) = \int_A p(x)\, dx
ということです。密度関数が指数の形をしているので,指数分布というわけですね。
\lambda の値を変化させて,確率密度関数 y=p(x) のグラフを描くと,以下のようになります。
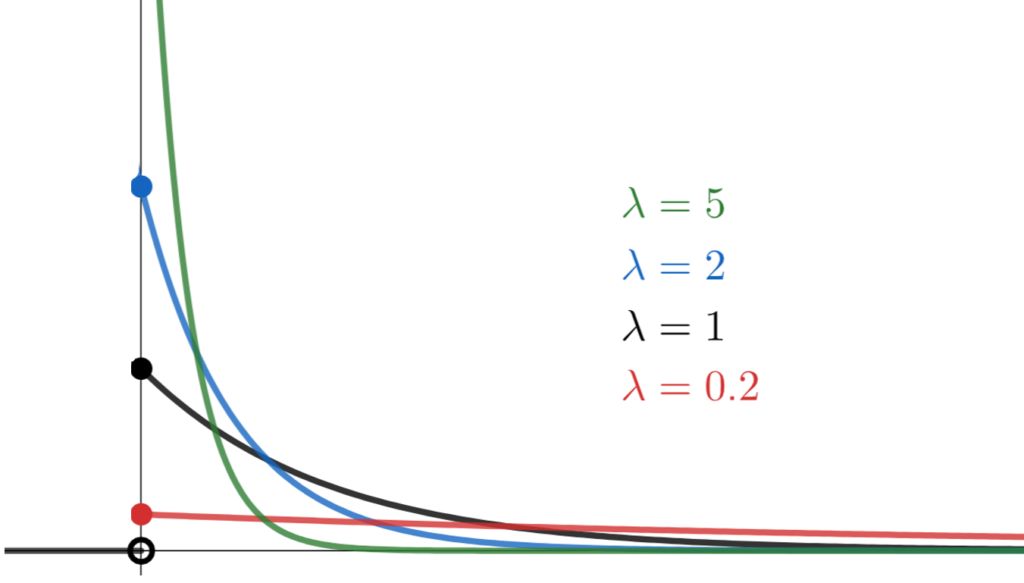
指数分布の例
指数分布は,「コールセンターに次に電話がかかってくるまでにかかる時間」や「次にこの交差点で事故が起こるまでにかかる時間」など,次に何かが起こるまでの時間を表す分布によく使われます。

後で紹介しますが,指数分布は無記憶性という,以下の重要な性質があります。
P(X>s+t\,|\,X>s) = P(X>t)
これはすなわち,今までのことは関係なく後のことが起こるといえます。先ほど挙げた,「コールセンターに次に電話がかかってくるまでにかかる時間」や「次にこの交差点で事故が起こるまでにかかる時間」というのは,まさに,「今までのこととは関係なく起こり得る事象」ですね。昨日コールセンターに電話が来ないからと言って,今日来るかどうかに関係ないわけです。
なお,無記憶性をもつ連続型の確率分布は,指数分布のみであることも知られています。なので,「無記憶性」すなわち「今までのこととは関係なく起こり得る事象」で,連続型の分布をモデル化したい場合は,指数分布が最も妥当であるというわけです。
指数分布の性質まとめ
まずは,紹介する指数分布の性質を,一気に列挙しましょう。
| 指数分布 \operatorname{Exp}(\lambda) | |
|---|---|
| 確率の型 | 連続型 |
| 確率密度関数 p(x) | \begin{cases} \lambda e^{-\lambda x } & x\ge 0,\\ 0 & x<0 \end{cases} |
| 累積分布関数 F(x)=P(X\le x) | \begin{cases} 0 & x< 0, \\ 1-e^{-\lambda x} & x \ge 0 \end{cases} |
| 確率 P(X>x) = 1-F(x) | \begin{cases} 1 & x< 0, \\ e^{-\lambda x} & x \ge 0 \end{cases} |
| 期待値(平均) E[X] | 1/\lambda |
| 分散 V(X) | 1/\lambda^2 |
| 標準偏差 \sqrt{V(X)} | 1/\lambda |
| 積率母関数 E[e^{tX}] | (1-t/\lambda)^{-1}, \,\, t<\lambda |
| 特性関数 E[e^{itX}] | (1-it/\lambda)^{-1} |
| 無記憶性 | P(X>s+t\,|\,X>s) = P(X>t) |
| 独立同分布な指数分布の和 | アーラン分布 |
| ポアソン分布との関係 | \sup\{n\mid X_1+\dots+X_n \le 1\} |
それぞれを,順番に掘り下げていきます。
指数分布の累積分布関数(分布関数)
指数分布の累積分布関数(分布関数)は,
\color{red}F(x)=\begin{cases} 0 & x< 0, \\ 1-e^{-\lambda x} & x \ge 0 \end{cases}
となります。これは,実際に
となることからわかります。グラフは,下のようになります。
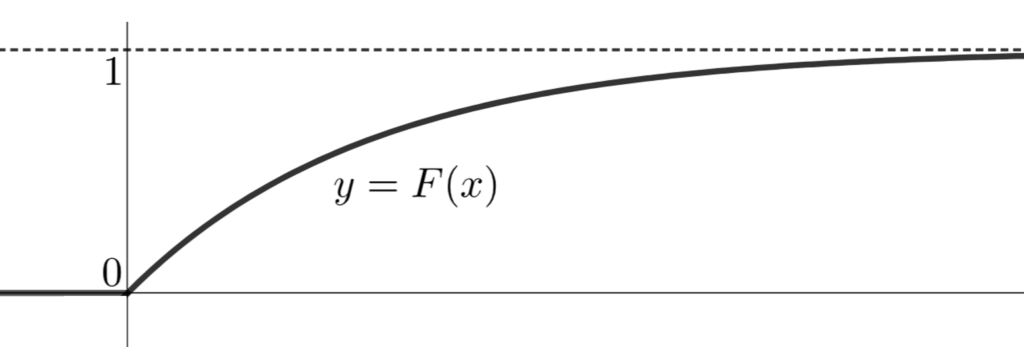
また, \lambda の値を色々変えてみると,累積分布関数は以下のように変わります。
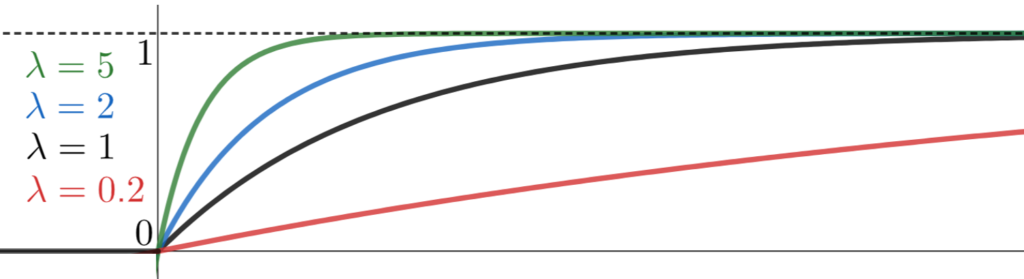
なお,このことから, P(X>x) = 1-F(x)=\begin{cases} 1 & x< 0, \\ e^{-\lambda x} & x \ge 0 \end{cases} も分かりますね。
指数分布の期待値(平均)・分散・標準偏差
定理(指数分布の期待値・分散・標準偏差)
X \sim \operatorname{Exp}(\lambda) とするとき, X の期待値・分散・標準偏差はそれぞれ
\color{red}\begin{aligned} E[X] &= \frac{1}{\lambda}, \\ V(X)&= \frac{1}{\lambda^2 } , \\ \sqrt{V(X)} &= \frac{1}{\lambda} \end{aligned}
である。
期待値と標準偏差がともに 1/\lambda になるわけですね。 \lambda \to 0+ とすると \infty に発散し, \lambda \to\infty とすると, 0 に収束します。
証明は,以下の記事で行っています。
指数分布の積率母関数・特性関数
定理(指数分布の積率母関数・特性関数)
X \sim \operatorname{Exp}(\lambda) とするとき, X の積率母関数・特性関数は,それぞれ
\color{red}\begin{aligned}E[e^{tX}]&=\frac{\lambda}{\lambda-t}, \quad t<\lambda, \\ E[e^{itX}]&=\frac{\lambda}{\lambda-it} \end{aligned}
である。
積率母関数・特性関数はそれぞれラプラス変換・フーリエ変換に対応しており,使い勝手もよいです。証明は,以下で行っています。
指数分布の無記憶性
定理(指数分布の無記憶性)
X を指数分布とするとき,
\color{red}P(X>s+t\,|\,X>s) = P(X>t)
である。これを,無記憶性 (lack of memory property) という。
逆に,連続型の確率分布において,無記憶性をもつ分布は指数分布に限る。
無記憶性をもつ,連続的なモデルを扱いたい場合は,指数分布を用いるのが最も適当である,というわけですね。
前半は明らかで,
\begin{aligned}P(X>s+t\,|\,X>s) &= \frac{P(X>s+t)}{P(X>t)} \\ &= \frac{e^{-\lambda (s+t)}}{e^{-\lambda s}}\\ &= e^{-\lambda t} \\ &= P(X>t) \end{aligned}
からわかります。詳しくは,以下の記事を参照してください。
独立同分布な指数分布の和はアーラン分布になる
定理(独立同分布な指数分布の和はアーラン分布)
X_1, X_2, \dots , X_n \sim \operatorname{Exp}(\lambda) を独立な確率変数とする。このとき,
\color{red} X_1 + X_2 +\cdots + X_n
は,パラメータ (\lambda, n ) のアーラン分布 (Erlang distribution) に従う。
アーラン分布については,別途記事にしましょう。
指数分布とポアソン分布の関係
指数分布とポアソン分布は,密接な関係にあります。
定理(指数分布とポアソン分布)
X_1,X_2,X_3,\ldots \sim \operatorname{Exp}(\lambda) を独立な指数分布とする。このとき,
\color{red}Y = \sup \{n \in \mathbb{N}\mid X_1 + X_2 +\dots + X_n \le 1\}
は,パラメータ \lambda のポアソン分布 (Poisson distribution) にしたがう。
指数分布をある意味「逆に見たもの」が,ポアソン分布なわけですね。
例を挙げると,コールセンターにおいて「次に電話が来るまでの時間」は指数分布でモデル化され,「ある一定時間に電話が来た回数」はポアソン分布でモデル化されるといった具合です。以下がその一例です。
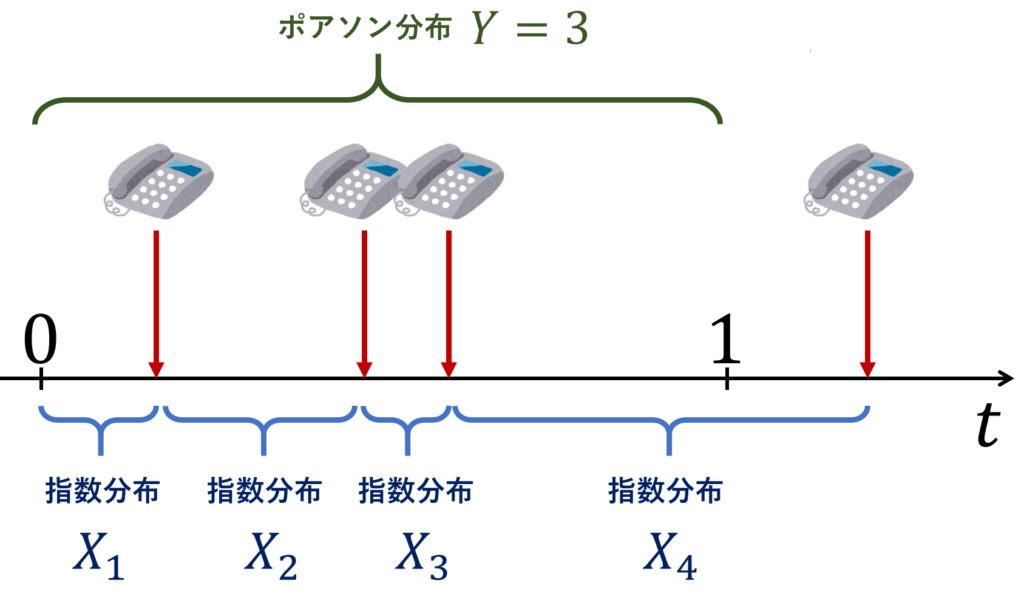
指数分布とポアソン分布は,「同じ現象の見方を変えたもの」と言えますね。