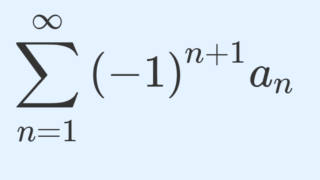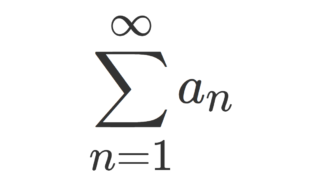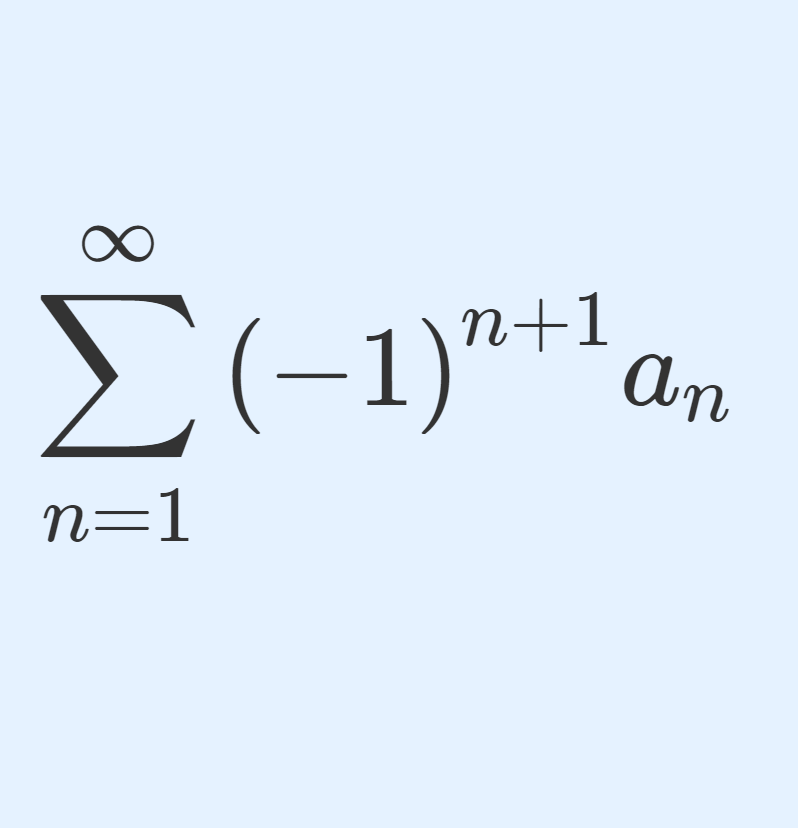数列 \{a_n\} に対し,\sum_{n=1}^\infty |a_n| が収束することを絶対収束 (absolutely convergence) といいます。級数が絶対収束すれば元の数列が収束することを,一つはコーシー列を使った一般的な方法で,もう一つは高校生にも理解できる方法で証明してみたいと思います。
級数が絶対収束すれば収束する
証明したい定理を改めて書いておきます。
定理(絶対収束 \implies 収束)
数列 \{a_n\} に対し,\sum_{n=1}^\infty |a_n| < \infty が成立するとき,級数 \sum_{n=1}^\infty a_n は収束する。
それでは証明していきましょう。
証明その1(コーシー列を用いた一般的な証明)
証明その1
m < n に対し,
\left| \sum_{k=m}^n a_k \right| \le \sum_{k=m}^n |a_k|である。絶対収束することから,\{ \sum_{k=1}^n |a_k| \}_n はコーシー列 (Cauchy sequence) であり,よって \{ \sum_{k=1}^n a_k \}_n もコーシー列である。故に,級数 \sum_{n=1}^\infty a_n は収束する。
証明終
理系の大学1年生で習う証明ですね。この証明は複素数の数列で適用可能なことに注意しましょう。
証明その2(高校生にも理解できる証明)
さて,2つ目の証明は高校生でも理解できると思われる証明です。こちらについては,数列 \{a_n\} は実数であるとします。
それでは,証明を見ていきましょう。
証明その2
\alpha = \sum_{n=1}^\infty |a_n| とおく。
b_n = \sum_{k=1}^n a_k + \sum_{k=n+1}^\infty |a_k|と定めると,数列 \{b_n\} は広義単調減少である。また,
b_n \ge \sum_{k=1}^n a_k - \sum_{k=n+1}^\infty |a_k| \ge - \sum_{n=1}^\infty |a_n| = -\alphaと,下から n に依存しない定数で抑えられているので,数列 \{b_n\} は下に有界。
このことより,極限 b = \lim_{n\to\infty} b_n が存在する。
b = \sum_{n=1}^\infty a_n となることを証明しよう。
\alpha = \sum_{k=1}^n |a_k| + \sum_{k=n+1}^\infty |a_k|より,
\sum_{k=n+1}^\infty |a_k| = \alpha - \sum_{k=1}^n |a_k| \xrightarrow{n\to\infty} \alpha - \alpha = 0に注意して,
\sum_{k=1}^n a_k = b_n - \sum_{k=n+1}^\infty |a_k|であり,両辺 n \to \infty として,
\sum_{k=1}^\infty a_k = b - 0 = bとなる。特に,級数 \sum_{n=1}^\infty a_n は収束することが証明できた。
証明終
少々テクニカルな証明ですが,無事に証明することができました。
逆は正しくない
逆に, \sum_{n=1}^\infty a_n が収束しても, \sum_{n=1}^\infty |a_n| が収束するとは限りません。このとき,級数は条件収束 (converge conditionally) するといいます。
たとえば,級数
\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdotsは \log 2 に収束しますが, \sum_{n=1}^\infty 1/n = \infty となります。
絶対収束しなくとも,正負の項が交互に現れる,かつある特定の条件をみたす交代級数であれば必ず条件収束することが知られています(上の例がそうです)。
これについては以下の記事を参照してください。